Занятие № 11. Интерполяция с кратными узлами и формула Эрмита

Рассмотрим задачу полиномиальной интерполяции функ­ции у= f(x) в более общей постановке.

Пусть на промежутке 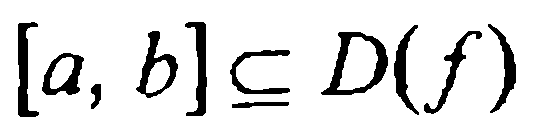расположены m+1 не­совпадающих узлов 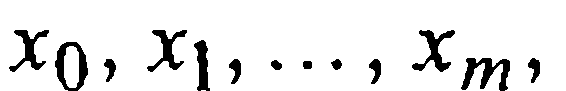и пусть в этих точках извест­ны значения у₀ = f(x₀), у₁=f(x₁,),..., у_т = f(x_m) данной функции, а также некоторые ее производные (максимальный по­рядок производных в разных узлах различен; в каких-то узлах производные могут быть вовсе неизвестны). Такие узлы будем называть кратными узлами. Конкретнее, будем считать, что за­даны:

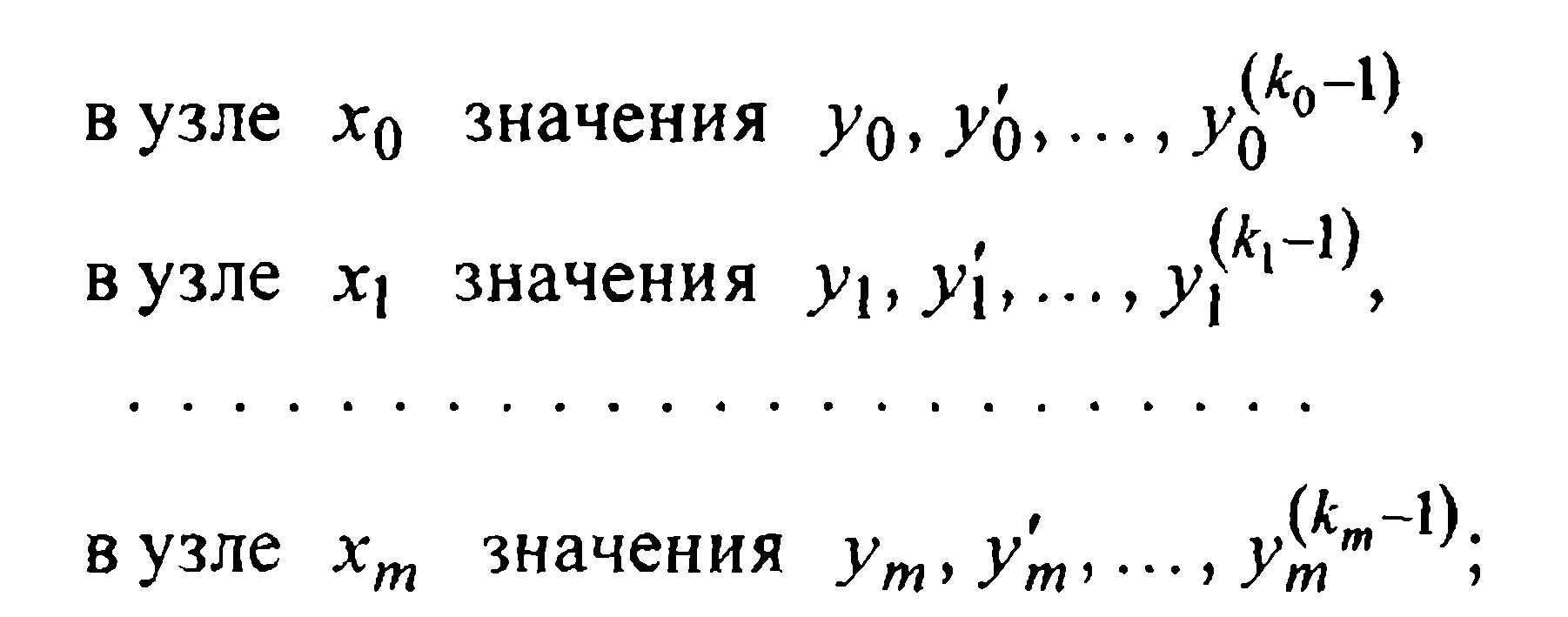(1)

тогда кратность узла x₀ считаетсяравной k₀, узла x₁ - k₁, …, узла x_m - k_m.

Предполагая, что суммарная кратность узлов есть

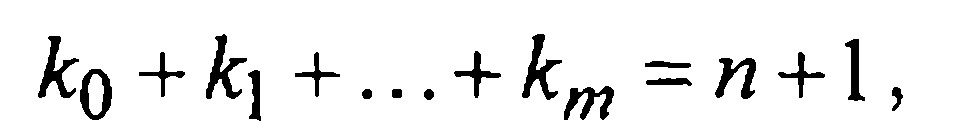(2)

ставим задачу построения многочлена Н_п(х) степени n (не вы­ше п) такого, что

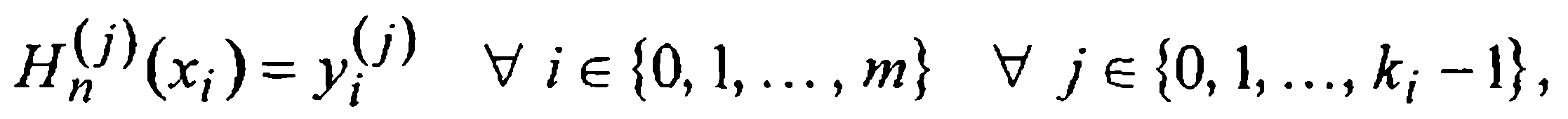(3)

где 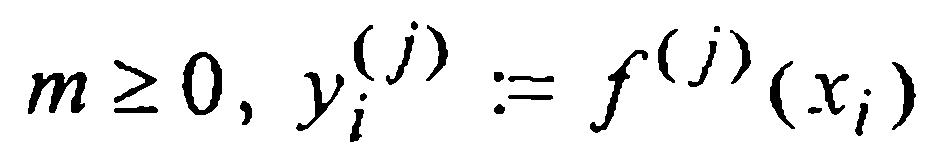— заданные посредством (1) значе­ния функции f(x) и ее производных и по определению считается 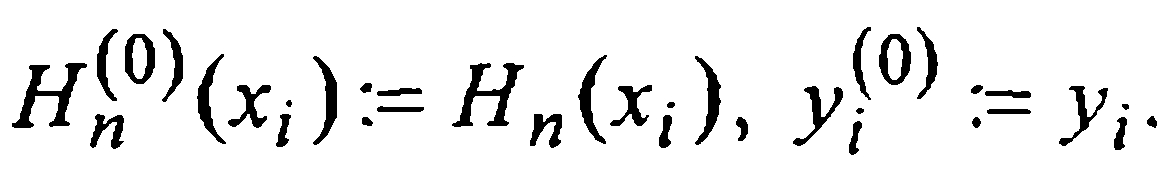Многочлен 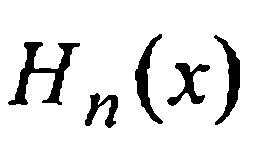будем называть интерполяционным многочленом Эрмита, а совокупность требований (3) — условиями эрмитовой интерполяции.

Формально можно считать, что нахождение такого много­члена состоит в том, чтобы однозначно определить п +1 коэффициентов a₀, а₁,..., а_п его канонического представления

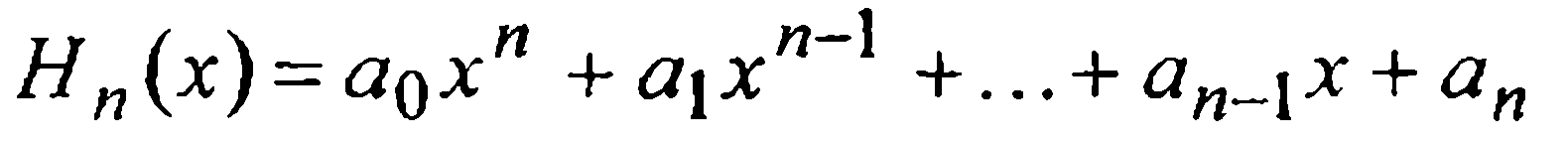(4)

из условий (3). В силу предположения (2) о суммарной кратности узлов эрмитовой интерполяции, совокупность требо­ваний (3) можно рассматривать как систему из п+1 уравне­ний относительно п+1 неизвестных — коэффициентов a_k мно­гочлена (4):

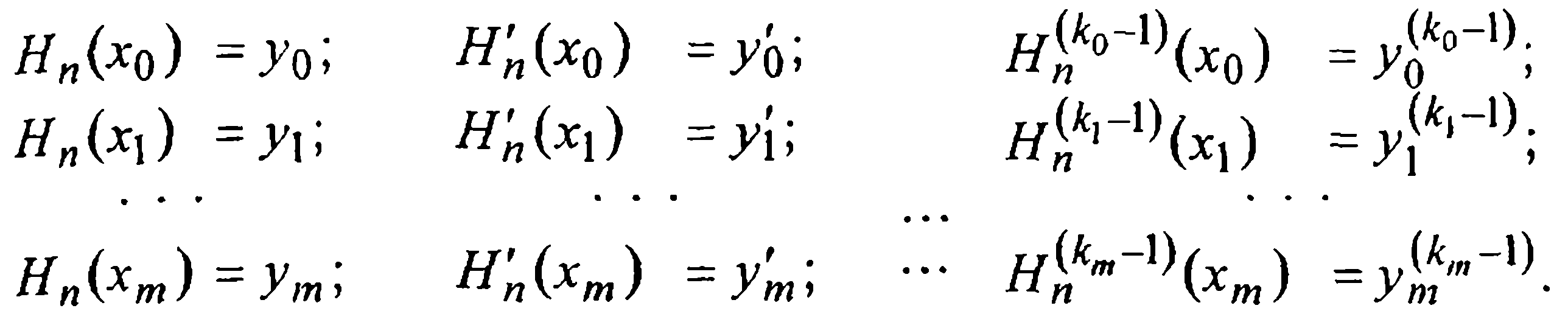
Выявление общего вида интерполяционных многочленов Эрмита Н_п(х) представляет непростую задачу и требует при­влечения определенных сведений из теории функций комплекс­ной переменной. Рассмотрим одну из возможных процедур фактического построения таких многочленов, не тре­бующую знания их общего вида.

Пусть L_m(x) — интерполяционный многочлен Лагранжа, построенный по данным т+1 значениям y_i = f(x i = 0,1,..., т. Будем пользоваться обо­значением 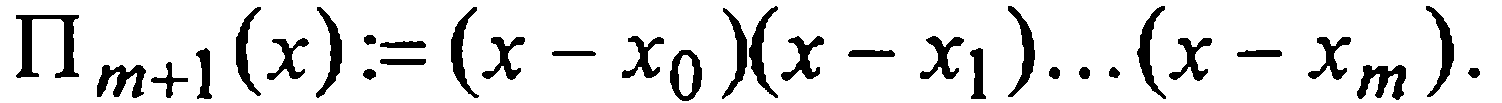Так как по ус­ловию т заведомо не превосходит п, то по теореме о делении многочлена с остатком искомый многочлен Эрмита Н_п(х) можно представить в виде

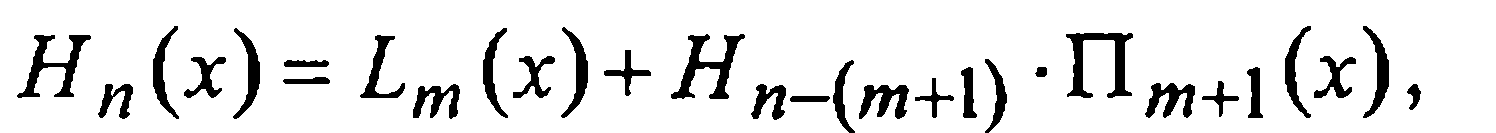(5)

где H_n-(m+1)(x) — некоторый неизвестный пока многочлен степени п-т-1.

Для построения многочлена H_n-(m+1)(x) будем привлекать информацию о производных данной функции, т.е. равенства 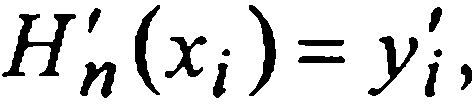в тех узлах х_i где первые производные, в соответ­ствии с (1), заданы (информация о самих значениях функции уже полностью исчерпана: в силу 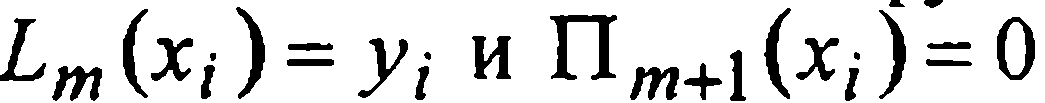для всех х_i от х₀ до х_m, согласно (5), будет и 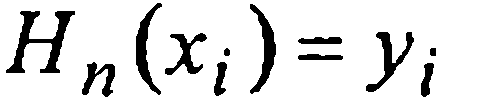при любых i∈{ 0,1,..., т}).

Продифференцировав равенство (5), имеем

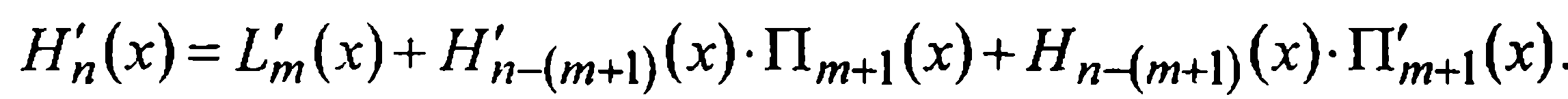(6)

Поскольку 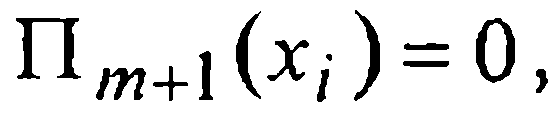в тех узлах х_i, где по условию эрмито­вой интерполяции справедливо 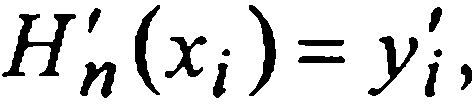можно записать

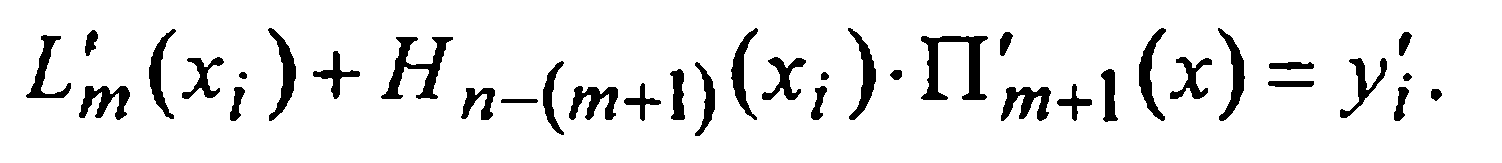
Отсюда выражаем значения многочлена H_n-(m+1)(x) в этих уз­лах:

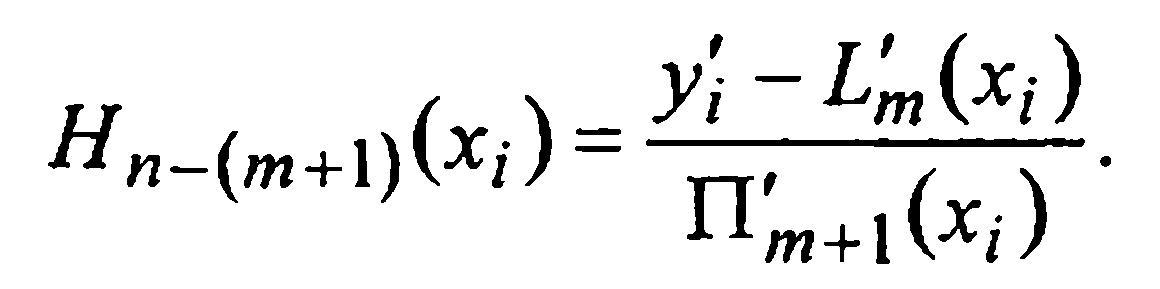
Правая часть этого равенства может быть вычислена; обо­значим ее через 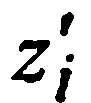. Таким образом, в ряде узлов х_i известны зна­чения многочлена H_n-(m+1)(x)= 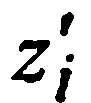, по которым этот многочлен однозначно восстанавливается обычной лагранжевой интерполя­цией, если в условиях (1) не содержится производных поряд­ка, выше первого (т.е. нет ни одного узла кратности больше 1); подстановка найденного многочлена H_n-(m+1)(x)в (5) приво­дит к искомому интерполяционному многочлену Эрмита. Если же в исходной информации (1) об f(x) имеются значения производных более высокого порядка, чем первый, то для вос­становления многочлена H_n-(m+1)(x) ставится задача эрмитовой же интерполяции, для чего наряду с полученными его значения­ми 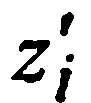, находят значения его производных путем дифференциро­вания равенства (6) (возможно неоднократного, в зависимости от максимального порядка заданных производных функции f(x)). Эта процедура построения интерполяционных многочле­нов Эрмита все более низких степеней продолжается до исчер­пывания всей информации (1) о функции и ее производных.

Рассмотрим реализацию описанного процесса эрмитовой интерполяции на простом примере, демонстрирующем возмож­ность восстановления многочлена n-й степени по его значениям и значениям некоторых его производных при суммарной кратно­сти узлов п+1.

Пример.Пусть сведения о некоторой функцииу= f(x) пред­ставлены следующей дискретной информацией:

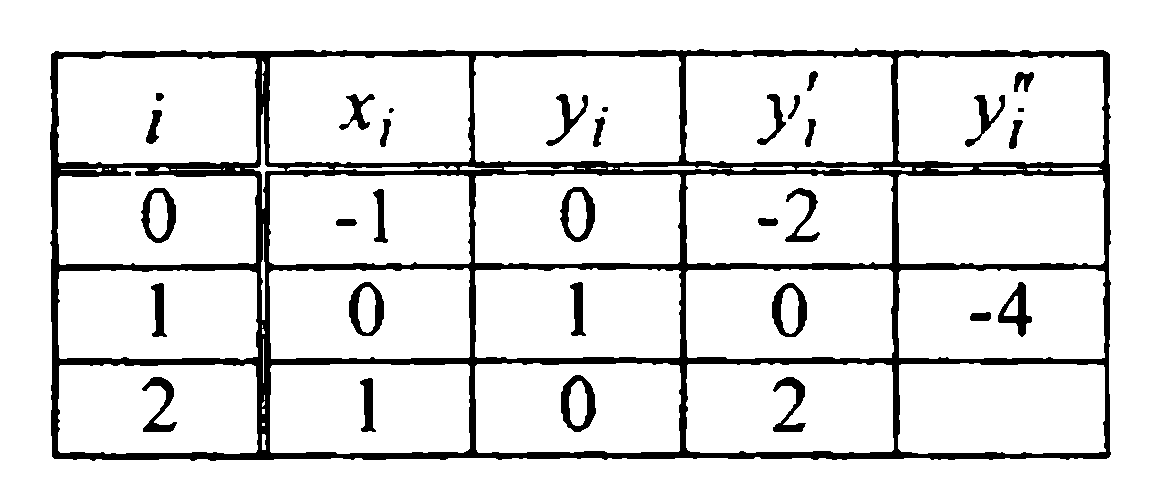
В соответствии с обозначениями (1) здесь: т=2;к₀-1 =1, k₁-1 =2,к₂-1=1 => п+1=к₀+к₁+к₂=7=>n=6.Таким образом, по данным сведениям о функции у =f(x),сосредоточенным в трех узлах 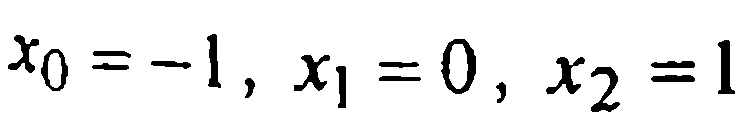кратности, соответственно, 2, 3, 2, следует строить интерполяционный многочлен Эрмита Н₆( х).

Согласно предложенной выше схеме, сначала, пользуясь столбцами 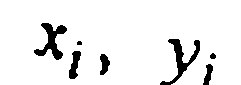таблицы данных, записываем интерполяционный многочлен Лагранжа второй степени

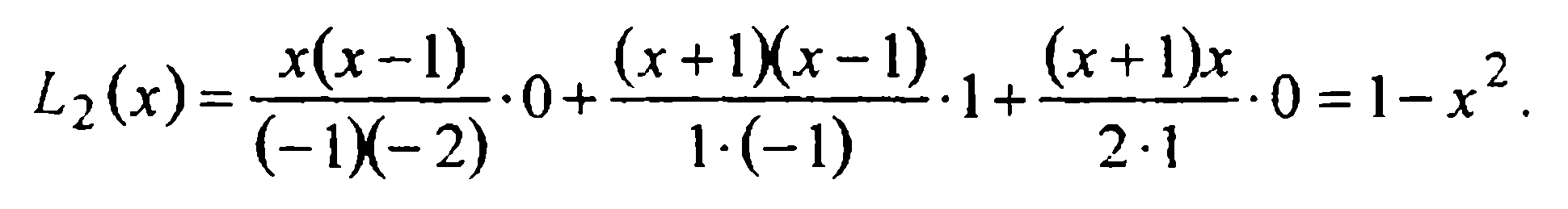
Далее по формуле (5) представляем Н₆(х) через L₂(x),H₃(x) и П₃(х):

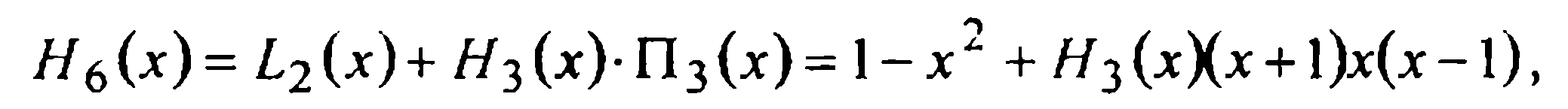(7)

и дифференцируем этот многочлен дважды:

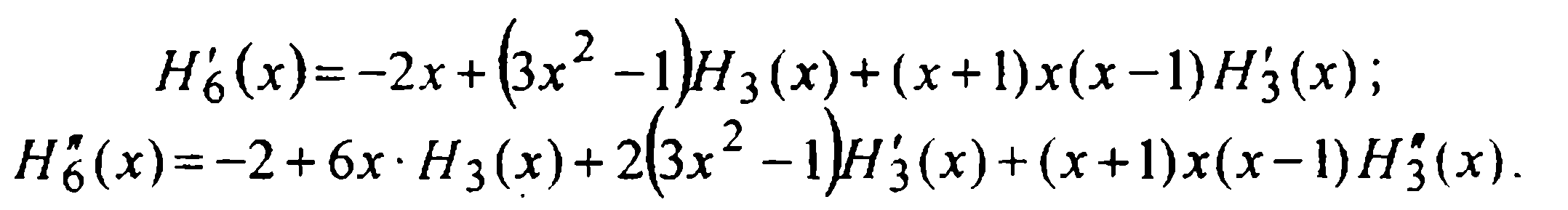
Подстановкой в 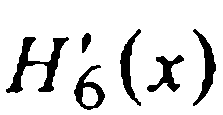значенийх=-1,х=0 и х=1 иприравниванием 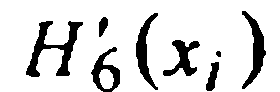заданным значениям 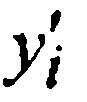получаем значения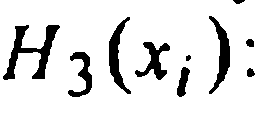

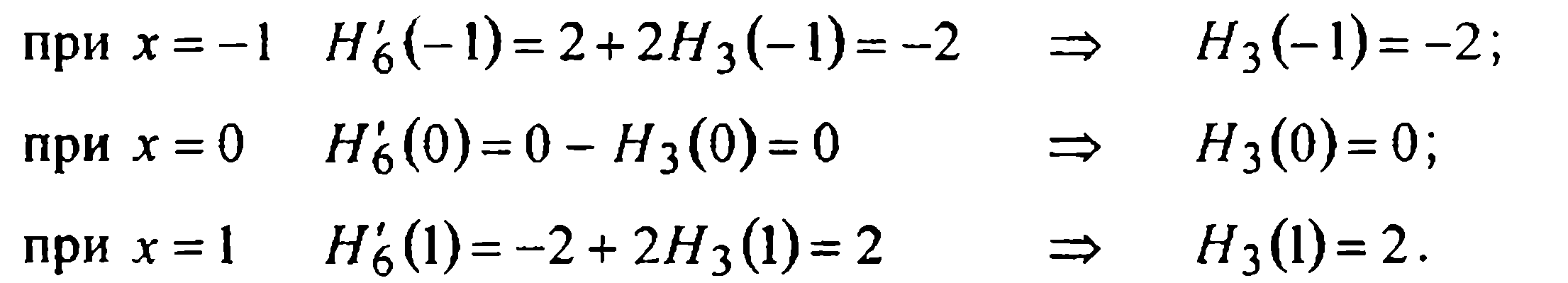
Учитывая их, из условия Я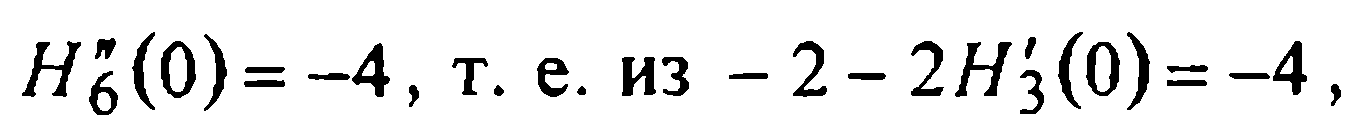находим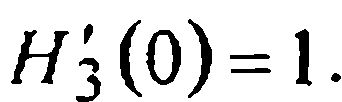

Итак, для выявления многочлена H₃(х) в (7) снова имеем задачу
эрмитовой интерполяции с данными, содержащимися в следующей
таблице:

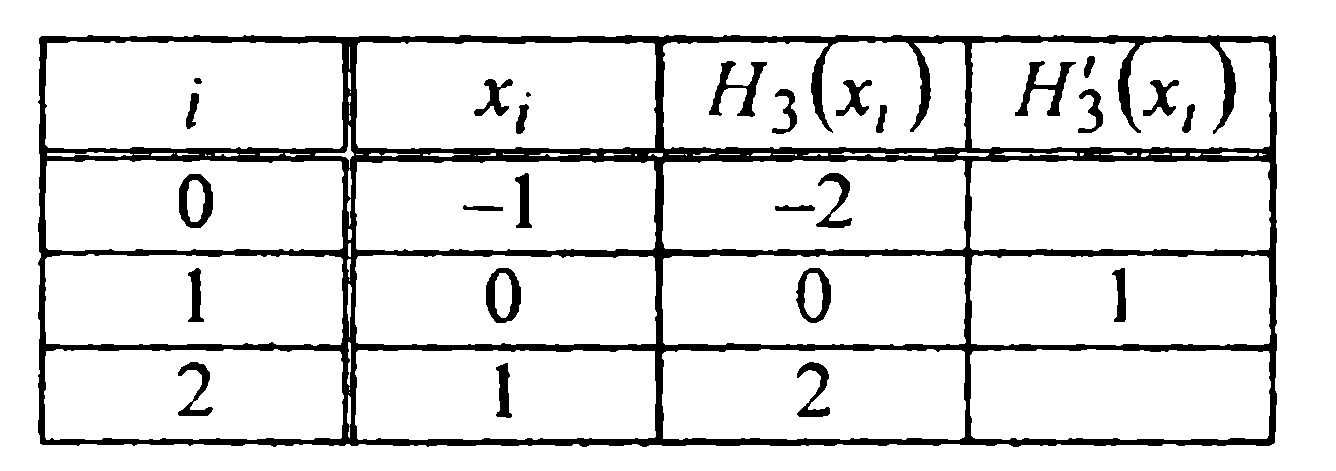
Здесь: 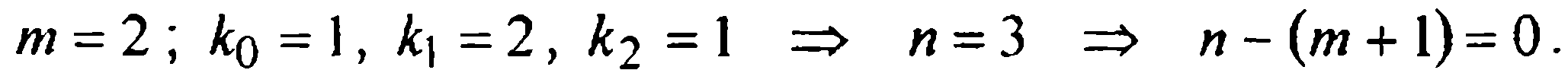В соот­ветствии с (5), для этого случая записываем:

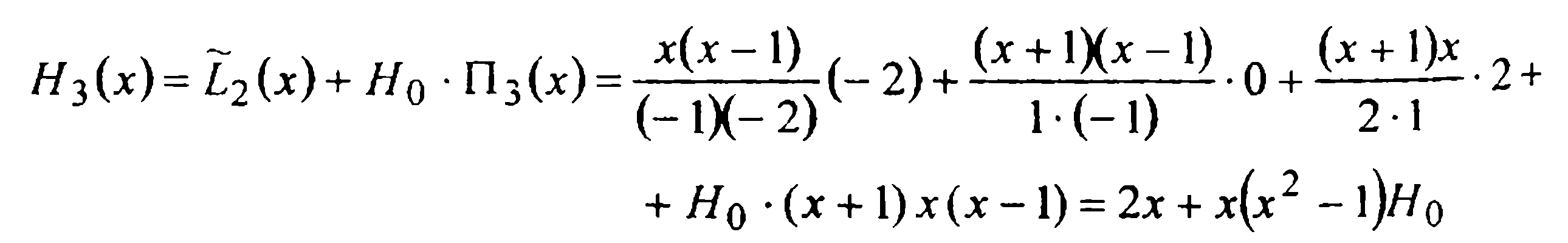
(где 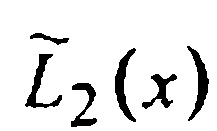— многочлен Лагранжа, интерполирующий функцию Н₃(х))-Остается найти постоянную H₀, для чего воспользуемся условием 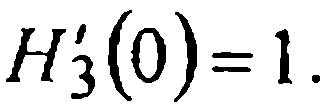Имеем:

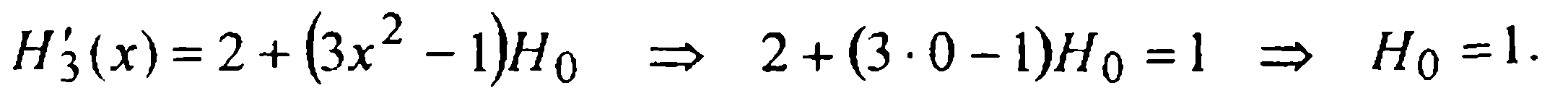
Следовательно,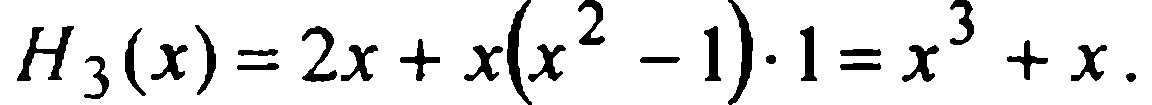

Подставив это в (7), получаем окончательное выражение искомого многочлена: