Скорость распространения упругих волн

Упругая волна – это механический процесс, который должен подчиняться второму закону Ньютона. Рассмотрим три примера определения скорости упругих волн.

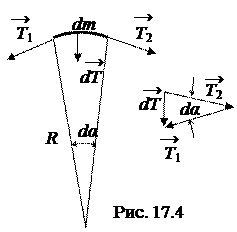1. Определим скорость распространения волны в струне, которая растянута силой Т. Пусть по струне бежит поперечная волна. Будем мысленно перемещаться вместе с некоторым бегущим изгибом волны в струне в форме «горбика» со скоростью волны (рис. 17.4). «Горбик бежит по струне, а частицы струны пробегают «горбик» и движутся почти по дуге окружности с центростремительным ускорением. Уравнение второго закона Ньютона для некоторого элемента примет вид .

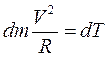Из треугольника сил 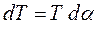. Масса «горбика» определим, умножив линейную плотность массы ρ на длину «горбика» 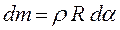. Подставив преобразования в уравнение второго закона Ньютона, получим для скорости распространения поперечной волны в формулу

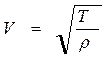. (17.6)

Чем сильнее натянута струна, тем скорость распространения волны будет больше.

2. Определим скорость распространения продольной волны в упругом стержне (рис.17.5). Для стержня справедлив закон Гука 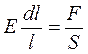: относительная деформация пропорциональна напряжению (отношение силы к площади сечения). Коэффициент пропорциональности Е называется модулем Юнга. Это характеристика упругих свойств материала. Пусть площадь сечения стержня S, плотность материала ρ.

Подействуем на свободный конец стержня силой F. Частицы стержня начнут движение с некоторой скоростью U. Фронт волны сжатия начнет распространяться по стержню со скоростью упругой волны V и за время dt сжатым будет участок длиной 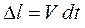. Величина сжатия участка будет равна произведению скорости движения частиц на время действия силы 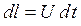. Отсюда получим, что отношение скорости смещения частиц к скорости распространения волны пропорционально отношению деформации участка к его длине: 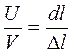. Подставив величину относительной деформации из закона Гука, получим соотношение между скоростями .

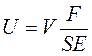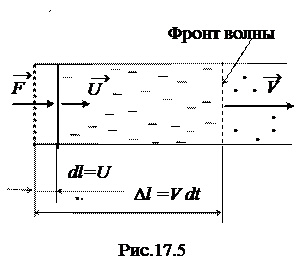Запишем уравнение второго закона Ньютона для участка стержня, пришедшего в движение: изменение импульса участка равно импульсу силы 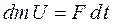. Массу участка определим как произведение плотности на объем 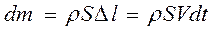. Подставив в уравнение второго закона Ньютона массу и скорости смещения, получим .

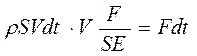Откуда после сокращения получим для фазовой скорости упругой продольной волны в стержне формулу

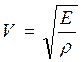. (17. 6)

Здесь Е – модуль Юнга, ρ – объёмная плотность материала. В металлах, благодаря высокой упругости, скорость звука составляет несколько километров в секунду.

3. Рассмотрим распространение звуковой волны в газе. Звук в газах − это процесс распространения областей сжатия – разрежения.

Пусть поршень, находящийся у основания трубки с площадью сечения S, начал движение с дозвуковой скоростью U. Частицы газа, прилегающие к поршню, приходят в движение с такой же скоростью. Воздух перед поршнем сжимается и сжатие передается последующим слоям. Граница между сжатым и невозмущенным газом, называемая фронтом, перемещается со скоростью звука V (рис. 17.6).

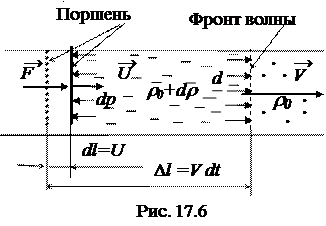Применим для определения скорости звука уравнение второго закона Ньютона для движущейся массы газа: 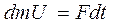(изменение импульса газа равно импульсу силы со стороны поршня)Массу газа определим как произведение плотности на объем: 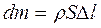, а силу давления на газ как произведение повышения давления на площадь: F = dpS. Примем, что отношение скоростей поршня и скорости фронта пропорционально отношению проходимых расстояний: 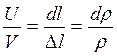, которое, в свою очередь, равно относительному изменению плотности газа. Подставив полученные преобразования в уравнение второго закона Ньютона, произведя замену Δl=Vdt, получим .

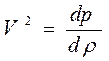Вследствие кратковременности процессы сжатия – разрежения газа в звуковой волне происходят адиабатически, без теплообмена между нагретой областью сжатия и охлажденной областью разрежения. Поэтому применим уравнение Пуассона 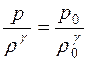. Дифференцируя 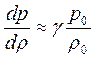, получим

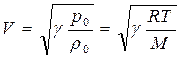. (17.7)

Здесь R = 8,31 Дж/ моль∙К – газовая постоянная, Т – абсолютная температура, М = 28,9 10 ^–3 кг/моль – масса моль воздуха, g = 1,4 – показатель адиабаты для двухатомных газов.