Математикалық ұғым

Математиканы оқытуда жаңа ақпараттар технологиялары мен компьютерді пайдалану

Математиканы оқытуда жаңа ақпараттар технологиялары мен компьютерді пайдалану (интерактивті тақталар, үлкейткіш проекторлар, тасымалдаушы құралдар, интернеттегі энциклопедилық материалдар, оқыту бағдарламалары, сайттар, т.б.) ерекше оын алады.

Математиканы оқытуда жаңа ақпараттар технологиялары мен компьютерді көрнекілік, нысандарды қозғалыста көрсету, есептеулерді жылдамдату, модельдер жасау, тексеру жұмыстарын оңайлату, оқушыларды қызықтыру үшін т.б. қолданылады. Бір сабақта санитарлық-гигиеналық талап бойынша 15 минуттан артық қолдануға болмайды

Осындай жаңа технологиялық әдістемелердің бірі оқытуда компьютерлік анимацияларды пайдалану. Анимацияны жасау үшін Flash-технологиясы қажет.

Flash – ағылшын тілінен аударғанда «найзағай», «жарық ету» дегенді білдіреді.

Әртүрлі үрдістерді көрсету үшін, математикалық тәуелділіктердің графиктерін, диаграммаларды, олардың қозғалысын көрсету үшін бұл таптырмайтын әдіс.

Flash-технологиясы математикалық есептеулер жүргізуге бағытталмаған, сондықтан мұнда күрделі математикалық есептеулер жүргізу қажет емес.

Математиканы оқытуда компьютерлік анимацияның көмегімен элементтердің көбін қозғалтуға болады: Мысалы: бөлшектердің алымдары мен бөлімдерін, олардың бүтін бөліктерін, толықтауыш көбейткіштерін, ортақ бөлімдерін, квадрат теңдеулердің графиктері арқылы түбірлерінің бар жоғын білу, дискриминанттың теріс, оң, ноль болу шарттарын; теңдеулер құру, матрицаларға амалдар қолдануда элементтерді орынан жылжыту, теңсіздіктердің шешімдерінің суреттерін қиылыстыру, теоремалар мен олардың дәлеледемелерін, суреттері мен графиктерін жылжыту арқылы дәлелдеуді көрнекілендіру, планиметриялық және стереометриялық есептер құру мен шығаруда белгісіздер мен есептің шартын түсіну, салу есептерінің шығарылу жолын көрсету т.б. Күрделілігі жоғары геометриялық есептерді шығарғанда дайын сызбаларды пайдаланудан гөрі, сызу үрдісін біртіндеп, логикалық үрдісте сызып отыру, түсінуге оңай екені белгілі. Міне, осы үрдісті компьютерлік анимация логикалық жүйе бойынша сыза отырып, есепті тез түсінуге, эстетикалық жағымды әсер алуға септігін тигізеді.

Математикадан білім беруде компьютерлік технологияларды сабақ үрдісінде пайдалана отырып, білім алушылардың математикалық, логикалық және оңтайлы ойлауын оятып, математика пәніне қызығушылыққа жетелейтін ғылыми мақсаты бар жаңа әдістеме.

Лекция.

Математикалық ұғымдар.

Жоспары:

1. Математикалық ұғым; .

2. Мазмұны мен көлемі;

3. Математикалық ұғымдарды анықтау.

4. Математикалық ұғымды бөлу және жіктеме.

Математикалық ұғым

Ұғым – зерттелінетін объектінің жалпы, сонымен бірге маңызды белгілерін сипаттайтын ойлау формасы.

Ұғым – өте күрделі логикалық және гносеологиялық категория. Ол біріншіден, жоғарғы материяның жемісі, екіншіден, ол шындық дүниені бейнелейді; үшіншіден, жалпылау құралы; төртіншіден, ұғымның қалыптасуы сөзбен, жазумен және белгілеулермен тығыз байланысты болады. Сонымен ұғым – ойлаудың жоғарғы түрі, шындық дүниесін сипаттайтын “қару” болып табылады.

Оқыту үрдісінде матиматикалық ұғымдардың пайда болуы мен құрылымы, олардың материалдық дүниенің заттарымен, құбылыстарымен байланысын ашу – мұғалімнің бірден-бір міндеті. Мұғалім бұл күрделі әдіснамалық (методологиялық) мәселені шешу нәтижесінде оқушылардың ғылыми дүние танымын қалыптастырады. Математика ақиқат (шындық) дүниенің белгілі бір жағы болып табылатын мөлшерлік қатынастар және кеңістіктік формалар, абстрактілі объектілер мен олар туралы ұғымдарды зерттейтін ғылым екендігін түсінуге мүмкіндік береді.

Ұғымның негізгі мінездемелері ретінде:

а) ұғымның мазмұны;

ә) ұғымның көлемі;

б) ұғымның басқа ұғымдармен қатысы және байланысы қарастырылады.

Ұғымның мазмұны деп ұғымдар класына жататын барлық объектілерге тиісті елеулі белгілердің жиынтығын айтады.

Ұғымның көлемі – берілген ұғымдар класына жататын барлық объектілер жиынтығы.

Мысалы, үшбұрыш ұғымының мазмұны “бір түзуде жатпайтын үш нүкте және оларды қос-қостан қосатын үш кесінді”, яғни үш қабырғасы, үш төбесі және үш бұрышы бар фигура болса, оның көлемі барлық тең қабырғалы, тең бүйірлі, әр қабырғалы үшбұрыштар бола алады.

Сол сияқты “функция” ұғымының мазмұны – аргументтің әрбір мәніне белгілі бір ереже немесе заң бойынша функцияның бір мәні сәйкес келуі болады. Оның көлеміне сызықтық функция, квадраттық функция, көрсеткіштік, логарифмдік функция т.б. жатады.

Сонымен ұғымның мазмұны – оның мәнді (елеулі) белгілері болады да, көлеміне ұғымға енетін барлық объектілер жиынтығы жатады.

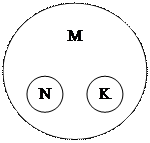
Ұғымның көлемін дұрыс елестету үшін оны “логикалық дөңгелек” арқылы кескіндеу тиімді. Мұндағы үлкен дөңгелек берілген ұғымды көрсетсе, оның ішіндегі кіші дөңгелектер берілген ұғымға жататындарын білдіреді. Мысалы, суретте үлкен дөңгелек жай бөлшек ұғымы (М) болса, оның ішіндегі дөңгелектер жай бөлшек ұғымына жататын дұрыс (N) бұрыс (K) бөлшектер болады.

Егер ұғымның көлемі көптеген ұғымдарды қамтитын болса, онда берілген ұғымның көлемі кең, ал ол ұғымдар аз болса, ұғымның көлемі тар делінеді. Егер ұғымның сәйкес класына енетін объектілердің артық, елеулі қасиеттері көп болатын болса, ұғымның мазмұны бай, ал ондай ортақ белгілер аз болса, ұғымның мазмұны кедей деп (аталады) аталынады.

Ұғымның көлемі мен мазмұны бір-біріне кері қатынаста болады, ұғымның көлемі кең болған сайын, оның мазмұны соғұрлым кедейлене береді, көлемі тарылған сайын, оның мазмұны байи түседі және керісінше.