Раздел: Электричество. Электромагнетизм

Контрольная работа № 3.

1. Две бесконечные параллельные плоскости заряжены с поверхностной плотностью заряда σ =2,8ּ10^-6 Кл/м² и расположены на расстоянии 8 см друг от друга. Определить напряженность электростатического поля внутри этих

плоскостей.

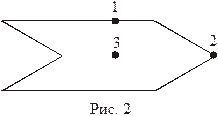
2. Металлическому полому телу, сечение которого представлено на рис. 2, сообщен отрицательный заряд. Каково соотношение между потенциалами точек 1, 2 и 3, если тело помещено во внешнее однородное электростатическое поле?

3. Имеется плоский воздушный заряженный конденсатор, отключенный от источника питания. Зазор между обкладками конденсатора заполняется диэлектриком с относительной диэлектрической проницаемостью ε =2,5. Как изменится при этом объемная плотность энергии электрического поля в зазоре?

4. Определить напряженность электрического поля в алюминиевом проводнике сечением 1,4 мм² при силе тока 1 А. Удельное сопротивление алюминия равно ρ_ал=28 нОм∙м.

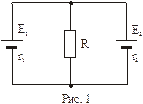
5. Два источника с ЭДС Е₁=2 В и Е₂=1,5 В и внутренними сопротивлениями r₁=0,5 Ом и r₂=0,4 Ом включены параллельно сопротивлению R=2 Ом (рис. 1). Определить силу тока через это сопротивление.

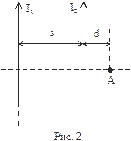6. По двум бесконечно длинным прямым параллельным проводам, находящимся на расстоянии s=10 см друг от друга в вакууме, текут токи I₁=20 А и I₂=30 А одинакового направления (рис. 2). Определить индукцию магнитного поля в точке А, отстоящей от тока I₂ на расстоянии d=3 см.

7. Определить мгновенное значение ЭДС самоиндукции, возникающей в цепи с индуктивностью L=25 мГн при изменении тока в ней по закону i=(3+4t)ּ10^-1 А.

8. Электромагнитная волна с частотой ν=4 МГц переходит из немагнитной среды с диэлектрической проницаемостью ε =3 в вакуум. Определить приращение ее длины.

9. Пластинку из эбонита (ε =3) расположили в однородном электростатическом поле с напряженностью Е=1 кВ/м перпендикулярно его силовым линиям. Определить поверхностную плотность связанных зарядов σ на поверхности пластинки.

10. Электростатическое поле создается сферой радиусом R=4 см, равномерно заряженной с поверхностной плотностью заряда σ =1 нКл/м². Определить разность потенциалов (φ₁-φ₂) между двумя точками поля, расположенными на расстояниях r₁=6 см и r₂=10 см от центра сферы.

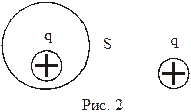11. Точечный заряд +q находится внутри сферической поверхности S (рис. 2). Если добавить заряд +q за пределами сферы, то как изменится поток вектора напряженности Е электростатического поля через эту поверхность?

12. Две концентрические проводящие сферы с радиусами R и 2R имеют заряды соответственно q₁=1 мкКл и q₂=2 мкКл. На расстоянии 3R от их центра потенциал электростатического поля φ =9000 В. Определить радиус сферы R.

13. Два конденсатора одинаковой ёмкости C₁=C₂= 5 мкФ соединены последовательно и присоединены к батарее с ЭДС 80 В. Определить заряд на каждом конденсаторе Q, энергию поля Wв каждом конденсаторе, напряженность поля Е между обкладками конденсаторов, если расстояние между нимиd= 2 мм. (Q₁ = 2×10^-4 Кл, W₁ = W₂ = 4 мДж, Е = 20 кВ/м)

14. Плоский конденсатор состоит из двух круглых пластин радиусом R= 5 см каждая. Расстояние между пластинами d = 2 мм. Конденсатор присоединен к источнику напряжения U= 60 В. Определить заряд Q, напряженность Е и энергию W поля конденсатора. (Q = 2 нКл, Е = 30 кВ/м, W = 60 нДж)

15. К пластинам плоского воздушного конденсатора приложена разность потенциалов U= 600B. Площадь пластин S= 100 см², расстояние между пластинамиd₁= 1,5 мм. Найти энергию конденсатора до и после раздвижения пластин до расстояния 3 мм, если источник напряжения перед раздвижением отключался. Как при этом изменяется напряженность Е электрического поля в конденсаторе? (W₁ = 10,6 мкДж, W₂ = 21,2 мкДж, Е₁ = Е₂)

16. По соленоиду, изготовленному из проводника диаметром d = 3 мм, протекает ток, создающий магнитное поле индукцией B = 6,3 мТл Определить силу тока, протекающего по плотно уложенным виткам соленоида. (I = 15A).

17. Токи силой I₁ = 10 A и I₂ = 2I₁ текут по бесконечно длинным прямым параллельным проводникам в противоположных направлениях. Расстояние между проводниками r = 10 см. Найти напряженность и индукцию магнитного поля в точке, находящейся на расстоянии r₁ = r₂ = r от токов I₁ и I₂. (Н = 27,6 А/м, В = 34,6 мкТл)

18.Два проволочных круговых витка радиусами r₁ = 2 см и r₂ = 20 см лежат в одной плоскости. По виткам протекают токи I₁ = I₂ в одном направлении. Напряженность магнитного поля в общем центре витков равна Н = 275 А/м. Определить силу тока в проводниках и индукцию магнитного поля. (I₁ = I₂ = 10 A, B = 345 мкТл)

19.Витки длинного соленоида, изготовленного из провода диаметром d = 5 мм, плотно прилегают друг к другу. Определить напряженность и индукцию магнитного поля внутри соленоида, если по соленоиду протекает ток I = 50 А. (Н = 10 кА/м, В = 12,56 мТл)

20.Два параллельных проводника длиной ℓ = 5 м каждый расположены на расстоянии d = 10 см друг от друга. По проводникам пропускают одинаковые токи I₁ = I₂ = 30 А. Определить силу взаимодействия F проводников. (F = 9 мН)

21. Два бесконечно длинных прямых проводника с токами I₁ = 5 A и I₂ = 3 A скрещены под прямым углом. Найти силу взаимодействия этих токов в точке, лежащей посередине между проводниками, если расстоянии между ними d = 5 см. (F = 0).

22. Найти угловую скорость вращения электрона по окружности в магнитном поле с индукцией В = 0,02 Тл. (w = 3,7×10⁹ рад/с)

23. Момент импульса электрона, вращающегося в магнитном поле с индукцией B = 30 мТл, равен L = 10×1,25^{-25 м}×кг²/с. Определить радиус окружности и угловую скорость электрона. (R = 0,5 см; w = 5,27×10⁹ с^-1).

24. Электрон движется в однородном магнитном поле с магнитной индукцией В = 0,5 Тл по окружности. Сколько оборотов N сделает электрон за время t = 1 c? (N = 14×10⁹ об)

25. Протон и a-частица влетают в однородное магнитное поле перпендикулярно линиям магнитной индукции. Сравнить радиусы окружностей, которые описывают частицы, если у них одинаковые скорости. (R_a/R_p = 2)

26. В однородном магнитном поле с индукцией В = 0,6 Тл движется прямой проводник длиной 0,4 м под углом 30⁰к линиям индукции, при этом на его концах возникает разность потенциалов U = 0,6B. Определить скорость движения проводника. (v = 5м/с)

27. Среднее значение ЭДС самоиндукции <|ℰ_сu,|> возникающее в соленоиде длиной 0,8 м, состоящего из 800 витков диаметром 2 см, равно 12,6 мВ. Определить скорость изменения силы тока в этом соленоиде. (DID/t = 40 А/с)

28. Два круговых контура радиусами R = 20 см и r = 2 мм расположены в одной плоскости так, что центры совпадают. Определить ЭДС индукции, возникающую в малом контуре, если в большом за 2 мс увеличивают ток от 0 до 10 А. (|ℰ_и| = 0,2 мкВ)

29. Электрическая емкость конденсатора в электромагнитном контуре С = 2 мкФ. Период колебаний Т = 1 мс. Определить индуктивность L катушки этого контура (L = 13 мГн)

30. Во сколько раз изменится период электромагнитных колебаний в контуре, если к конденсатору контура параллельно подсоединить еще один конденсатор, емкость которого в 8 раз больше? (Т₂/Т₁ = 3)

31. Сила тока в колебательном контуре изменяется по закону 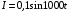, А. Индуктивность контура 0,1 Гн. Найти закон изменения напряжения на конденсаторе и его емкость. ( 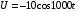, С = 10 мкФ)

32. В однородном магнитном поле с индукцией 100 мкТл движется электрон по спирали. Радиус витков спирали 5 см, а расстояние между центрами витков 20 см. Определить скорость электрона.

. Раздел:. Раздел: Волновая и квантовая природа излучения. Раздел: Атом водорода. Элементы квантовой механики.

Контрольная работа) № 4. _

1. На дифракционную решетку падает нормально параллельный пучок белого света. Спектры третьего и четвертого порядка частично накладываются друг на друга. На какую длину волны в спектре четвертого порядка накладывается граница ( = 780 нм) спектра третьего порядка?

2.На дифракционную решетку, содержащую n = 600 штрихов на миллиметр, падает нормально белый свет. Спектр проецируется на экран линзой, помещенной вблизи решетки. Определить длину (l)спектра первого порядка на экране, если расстояние от линзы до экрана L = 1,2 м. Границы видимого спектра λ_кр = 780 нм, λ_ф = 400 нм.

3..Свет с длиной волны 0,6 мкм нормально падает на тонкую пленку, нанесенную на стеклянную поверхность. Вследствие интерференции отраженные от различных поверхностей пленки световые волны будут гасить друг друга. Определить минимальную разность хода этих волн.

4. На непрозрачную пластину с узкой щелью падает нормально плоская монохроматическая световая волна (λ= 600 нм). Угол отклонения лучей, соответствующих второму дифракционному максимуму, φ=2 0°.Определить ширину (а) щели.

5. Пучок света последовательно проходит через два николя, плоскости пропускания которых образуют между собой угол φ= 4 0°. Принимая, что коэффициент поглощения (k)каждого николя равен 0,15, найти, во сколько раз пучок света, выходящий из второго николя, ослаблен по сравнению с пучком, падающим на первый николь.

6. Угол падения луча на поверхность стекла равен i₁= 60°. При этом отраженный пучок света оказался максимально поляризованным.Определить угол (i₂)преломления луча.

7.Угол между плоскостями пропускания поляроидов равен φ = 50°. Естественный свет, проходя через такую систему, ослабляется в n= 4 раза. Пренебрегая потерей света при отражении, определить коэффициент поглощения (k) света в поляроидах.

8.Пучок света, идущий в стеклянном сосуде с глицерином, отражается от дна сосуда. При каком угле (i₁) падения отраженный пучок света максимально поляризован?

9. Из смотрового окошечка печи излучается поток P_e = 4кДж/мин. Определить температуру (T) печи, если площадь окошечка S= 8 см².

10. Поток излучения абсолютно черного тела _e = 10 кВт, максимум энергии излучения приходится на длину волны λ_m= 0,8 мкм. Определить площадь (S) излучающей поверхности.

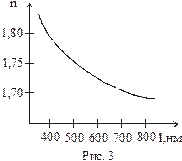
11. На графике (рис. 3) изображена зависимость показателя преломления стекла n от длины волны света l. Одинаковы ли дисперсии красного и синего света в стекле? Как это отражается на спектре видимого света, полученном с помощью стеклянной призмы?

12. На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения. Расстояние d между атомными плоскостями равно 280 пм. Под углом φ = 65° к атомной плоскости наблюдается дифракционный максимум первого порядка. Определить длину волны (λ) рентгеновского излучения.

13. Как и во сколько раз изменится поток излучения абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра (λ_m1= 780 нм) на фиолетовую λ =160 нм. Красная граница фотоэффекта для цинка λ₀= 310нм. Определить максимальную кинетическую энергию (Т_max) фотоэлектронов в электрон-вольтах, если на цинк падает свет с длиной волны λ = 200 нм.

14. На поверхность калия падает свет с длиной волны λ= 150 нм. Определить максимальную кинетическую энергию (Т_max) фотоэлектронов.

15. Фотон с энергией E = 10 эВ падает на серебряную пластину и вызывает фотоэффект. Определить импульс (р), полученный пластиной, если принять, что направления движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластин.

16. На фотоэлемент с катодом из лития падает свет с длиной волны λ = 200 нм. Найти наименьшее значение задерживающей разности потенциалов (U_min), которую нужно приложить к фотоэлементу, чтобы прекратить фототок.

17. Какова должна быть длина волны γ-излучения, падающего на платиновую пластину, если максимальная скорость фотоэлектронов V_max = 3 Мм/c?

18. На металлическую пластину направлен пучок ультрафиолетового излучения (λ = 0,25 мкм). Фототок прекращается при минимальной задерживающей разности потенциалов U_min = 0,96 В. Определить работу выхода (А) электронов из металла.

19. Фотон с длиной волны λ ₁ = 15 пм рассеялся на свободном электроне. Длина волны рассеянного фотона λ ₂ = 16 пм. Определить угол (φ) рассеяния.

20. Вычислить по теории Бора радиус (r₂) второй стационарной орбиты и скорость (V₂)электрона на этой орбите для атома водорода.

21. Вычислить по теории Бора период (T)вращения электрона в атоме водорода, находящегося в возбужденном состоянии, определяемом главным квантовым числом n = 2.

22. Определить максимальную энергию (E_max) фотона серии Бальмера в спектре излучения атомарного водорода.

23. Определить первый потенциал (E₁)возбуждения и энергию ионизации (E_i)атома водорода, находящегося в основном состоянии.

24. Определить энергию (E)фотона, испускаемого атомом водорода при переходе электрона с третьей орбиты на вторую.

25. Найти наибольшую (E_max) и наименьшую (E_min)длины волн в ультрафиолетовой серии водорода (серия Лаймана).

26. В однозарядном ионе гелия электрон перешел с третьего энергетического уровня на первый. Определить длину волны (λ) излучения, испущенного ионом гелия.

27. Электрон в атоме водорода находится на третьем энергетическом уровне. Определить кинетическую (Т), потенциальную (П) и полную (Е) энергии электрона. Ответ выразить в электронвольтах .

28. Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике находится в основном состоянии. Какова вероятность (p)обнаружения частицы в крайней четверти ящика?

29. Атом испустил фотон с длиной волны λ= 800 нм. Продолжительность излучения τ = 10 нс. Определить наибольшую точность (Δλ), с которой может быть измерена длина волны излучения.

30. Используя соотношение неопределенностей, оценить ширину (I) одномерного потенциального ящика, в котором минимальная энергия электрона E_min = 10 эВ.

31. Альфа-частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Используя, соотношения неопределенностей, оценить ширину (l)ящика, если известно, что минимальная энергия частицы E_min = 8 МэВ.

32. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l. В каких точках в интервале 0 < х< l плотности вероятности нахождения электрона на втором и третьем энергетических уровнях одинаковы? Вычислить плотность вероятности для этих точек. Решение пояснить графиком.

33. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l = 0,1 нм. Определить в электрон-вольтах наименьшую разность энергетических уровней электрона.

Разработчик(и):

Профессор, д.т.н., профессор				Шульц А.Н.
(должность, ученая степень, ученое звание)		(подпись)		(Ф.И.О.)
(должность, ученая степень, ученое звание)		(подпись)		(Ф.И.О.)
		« __ » ________ 201_ г.