Основные уравнения математической физики

Система уравнений (1.47 - 1.49) остается бесконечно сложной, во-первых, из-за большого количества скалярных уравнений (в трехмерном координатном пространстве получается 9 уравнений движения и 27 уравнений, описывающих граничные условия), во-вторых, из-за нарушения непрерывности функций на границе раздела сред, что приводит, как правило, к невозможности применения простых численных методов для решения задач. Поэтому при моделировании различных физических процессов предполагают, что описываемые среды имеют постоянные входные параметры, хотя бы на каком-то конечном отрезке. Для типовых процессов, как правило, это параметры теплопроводности, температуропроводности, теплоемкости, для процессов упругих колебаний, как правило, постоянными предполагаются модули Юнга, для процессов, связанных с фазовыми переходами постоянной предполагается энергия Гиббса и т.д.

В этом случае преобразование уравнений (1.47 - 1.49) при­водит к более простым дифференциальным и интегральным уравнениям или даже к интегро-дифференциальным уравнениям. При этом весьма широкий класс физических процессов описывается линейными дифференциальными уравнениями второго порядка.

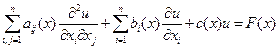(1.53)

Основные системы дифференциальных уравнений принято разделять по тем областям, где они были впервые сформулированы. Однако не следует забывать, что мы имеем дело с обобщенными потоками, и эти уравнения справедливы и для других областей, если обобщенный поток можно записать, используя постоянные параметры среды. Таким образом, уравнения тепломассопереноса могут описывать как уравнения переноса массы, уравнения переноса энергии, так и поток денег в банке, а волновое уравнение может описывать электромагнитное поле так же, как и волну в плазме или в волну тепла, распространяющегося по трубе с жидкость.

В этом параграфе мы рассмотрим характерные физические про­цессы, сводящиеся к различным краевым задачам для дифферен­циальных уравнений.

1. Уравнение колебаний.Многие задачи механики (коле­бания струн, стержней, мембран и трехмерных объемов) и физики (электромагнитные колебания) описываются уравнением колебаний вида

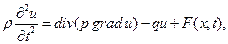(1.54)

где неизвестная функция и(х,t) зависит от п (п = 1,2,3) пространст­венных координат х = (x₁, x₂ ,….. ,х_п) и времени t; коэффициенты r, р и q определяются свойствами среды, где происходит колебательный процесс; свободный член F(x,t) выражает интенсивность внешнего возмущения. В уравнении (1.54) в соответствии с определением опера­торов div и grad

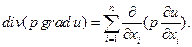
Продемонстрируем вывод уравнения (1.54) на примере малых попе­речных колебаний струны. Струной называется натянутая нить, не сопротивляющаяся изгибу. Пусть в плоскости (х,и) струна совершает малые поперечные колебания около своего положения равновесия, совпадающего с осью х. Величину отклонения струны от положения равновесия в точке х в момент времени t обозначим через u(x,t), так что u = и(х, t) есть уравнение струны в момент времени t. Ограничиваясь рассмотрением лишь малых колебаний струны, мы будем пренебрегать величинами высшего порядка малости по сравнению с tg a = ди/дх.

Рис.1.1.

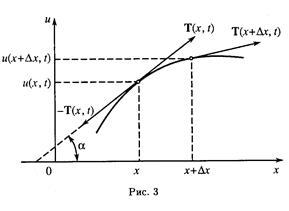
Так как струна не сопротивляется изгибу, то ее натяжение Т(х, t) в точке х в момент времени t направлено по касательной к струне в точке х (рис.1.1).

Любой участок струны (а,b) после отклонения от положения равновесия в рамках нашего приближения не изменит своей длины:

Рис. 1.1

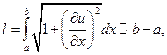
и, следовательно, в соответствии с законом Гука величина натяже­ния |Т(х,t)| будет оставаться постоянной, не зависящей от х и t, |Т(х,t)| = T₀. Обозначим через F(x,t) плотность внешних сил, дейст­вующих на струну в точке х в момент времени t и направленных перпендикулярно оси х в плоскости (х,и). Наконец, пусть р(х) обо­значает линейную плотность струны в точке х, так что приближен­но р(х)Dх — масса элемента струны (х,х + Dх).

Составим уравнение движения струны. На ее элемент (х, х +Dх) действуют силы натяжения Т(х + Dх,t), -T(x,t) (см. рис. 1.1) и внешняя сила, сумма которых согласно законам Ньютона должна быть равна произведению массы этого элемента на его ускорение, так что

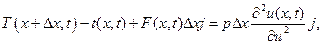
где единичный вектор j направлен вдоль оси u. Проектируя это век­торное равенство на ось u, на основании всего сказанного получим равенство

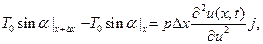(1.55)

Но в рамках нашего приближения

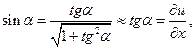
а потому из (1.55) имеем

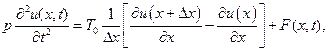
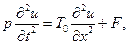(1.56)

Это и есть уравнение малых поперечных колебаний струны.

При F¹0 колебания струны называются вынужденными,

а при F = 0 - свободными.

Если плотность р постоянна, р(х) = р, то уравнение колебаний струны принимает вид

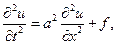(1.57)

где f = F/p, a a² = T₀/p — постоянная. Уравнение (1.57) мы будем так­же называть одномерным волновым уравнением.

Уравнение вида (1.54) описывает также малые продольные колеба­ния упругого стержня

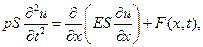(1.58)

где S(x) — площадь поперечного сечения стержня и Е(х) — модуль Юнга в точке х.

Из физических соображений следует, что для однозначного опи­сания процесса колебаний струны или стержня необходимо дополни­тельно задать смешения, скорости в начальный момент времени (начальные условия) и режим на концах (граничныеусловия).

Аналогично выводится уравнение малых поперечных колебаний мембраны

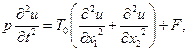(1.59)

Если плотность р постоянна, то уравнение колебаний мембраны

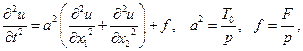(1.60)

будем называть двумерными волновым уравнением. Трехмерное волновое уравнение

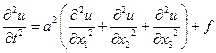(1.61)

описывает процессы распространения звука в однородной среде и электромагнитных волн в однородной непроводящей среде. Этому уравнению удовлетворяют плотность газа, его давление и потенци­ал скоростей, а также составляющие напряженности электрического и магнитного полей и соответствующие потенциалы.

Мы будем записывать волновые уравнения (1.57), (1.60) и (1.61) единой формулой

2. Уравнение диффузии. Процессы распространения тепла или диффузии частиц в среде описываются следующим общим урав­нением диффузии:

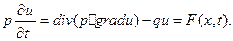(1.62)

Выведем уравнение распространения тепла. Обозначим через u(x,t) температуру среды в точке 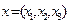в момент време­ни t. Считая среду изотропной, обозначим через р(х), с(х) и r(x) со­ответственно ее плотность, удельную теплоемкость и коэффициент теплопроводности в точке х. Обозначим через F(x,t) интенсивность источников тепла в точке х в момент времени t. Подсчитаем баланс тепла в произвольном объеме V за промежуток времени (t,t + Dt). Обозначим через S границу V, и пусть n — внешняя нормаль к ней. Согласно закону Фурье через поверхность S в объем V поступает количество тепла

равное в силу формулы Гаусса-Остроградского:

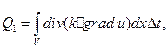
За счет тепловых источников в объеме V возникает количество тепла

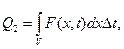
Так как температура в объеме V за промежуток времени (t, t + Dt) выросла на величину:

то для этого необходимо затратить количество тепла:

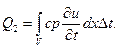
С другой стороны, 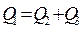, и потому:

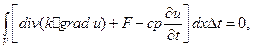
откуда в силу произвольности объема V получаем уравнение распространения тепла:

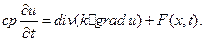(1.63)

Если среда однородна, т. е. с, р и k — постоянные, то уравнение (1.63) принимает вид:

(1.64)

Уравнение (1.64) называется уравнением теплопроводности. Число п пространственных переменных x₁, х₂,..., х_n в этом уравнении может быть любым.

Как и в случае уравнения колебаний, для полного описания про­цесса распространения тепла необходимо задать начальное распределение температуры u в среде (начальное условие) и режим на границе этой среды (граничное условие).

Аналогично выводится и уравнение диффузии частиц. При этом вместо закона Фурье нужно пользоваться законом Нэрнста для потока частиц через элемент поверхности DS за единицу времени: 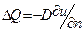, где D(x) - коэффициент диффузии и u(x,t) - плотность частиц в точке х в момент времени t. Уравнение для плотности и будет иметь вид (1.62), где р обозначает коэффициент пористос­ти, р = D и q характеризует поглощение среды.

3. Стационарное уравнение.Для стационарных процессов F(x, t) = F(x), u(х,t) = u(х) уравнения колебания (1.54) и диффузии (1.62) принимают вид

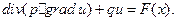(1.65)

При р = const и q = 0 уравнение (1.65) называется уравнением Пуассона:

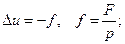(1.66)

при f =0 уравнение (1.66) называется уравнением Лапласа:

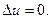(1.67)

Для полного описания стационарного процесса необходимо еще задать режим на границе — одно из граничных условий (14)-(16).

Пусть в волновом уравнении (10) внешнее возмущение f(x,t) периодическое с частотой w и амплитудой a² f(x):

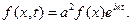
Если искать периодические возмущения u(x,t) с той же частотой и неизвестной амплитудой u(x),

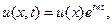
то для функции u(х) получим стационарное уравнение

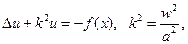(1.68)

называемое уравнением Гелъмгольца.

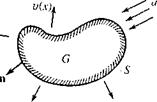
Рис. 1.2

К краевым задачам для уравнения Гельмгольца приводят задачи на рассеяние (дифракцию). Например, пусть задана приходящая (из бесконечности) плоская волна которая подвергается изменению из-за наличия некоторого препятствия на грани­це S ограниченной области G (рис. 1.2). Препятствие можно задавать, например, с помощью условия:

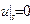
или

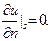
Это препятствие порожда­ет рассеянную волну v(x). Эта волна вдали от рассеивающих центров будет близка к расходящейся сферической волне

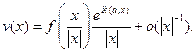(1.69)

Поэтому при 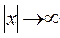волна v(x) должна удовлетворять условиям вида

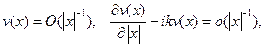(1.70)

называемым условиями излучения Зоммерфельда.

Суммарное же возмущение u(х) вне области G складывается из плоской и рассеянной волн:

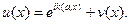(1.71)

Отметим попутно, что функция 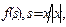фигурирующая в (1.69), называется амплитудой рассеяния. Она зависит, кроме того, от падающего импульса ka.

4. Уравнения газо-гидродинамики. Рассмотрим движение идеальной жидкости (газа), т.е. жидкости, в которой отсутствуют силы вязкости. Пусть V(x,t) = (v₁,v₂,v₃) - вектор скорости движе­ния жидкости, p(x,t) - ее плотность,

p(x,t) - давление, f(x,t) - интенсивность источников и вектор

F(x,t) = (F₁, F₂, F₃) - интенсивность массовых сил. Тогда эти величины удовлетворяют следующей (нелинейной) системе уравнений, называемых уравнениями гидроди­намики (газовой динамики):

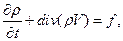(1.72)

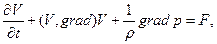(1.73)

Уравнения (1.72) и (1.73) называются соответственно уравнением неразрывностииуравнением движения Эйлера. Чтобы замкнуть эту систему уравнений, необходимо еще задать связь между давлением и плотностью:

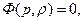(1.74)

так называемое уравнение состояния. Например, для несжимаемой жидкости уравнение состояния имеет вид r = const, а для адиабати­ческого движения газа -

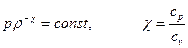
где c_p и c_v - удельные теплоемкости газа при постоянном давлении и постоянном объеме соответственно.

В частности, если жидкость несжимаема (r =const) и ее движение потенциально (V = - grad u), то из уравнения неразрывности (1.72) следует, что потенциал и удовлетворяет уравнению Пуассона (1.66).

5. Уравнение Максвелла. Пусть в некоторой среде имеется переменное электромагнитное поле.

Обозначим:

E(x,t) = (E₁, E₂, E₃) - напряженность электрического поля;

H(x,t) = (H₁, H₂, H₃) - напряженность магнитного поля;

r(х) - плотность зарядов; e - диэлектрическая постоянная среды;

m - коэффициент магнитной проницаемости среды;

I(x,t) = (I₁, I₂, I₃ ) - ток проводимости.

Тогда эти величины удовлетворяют следующей (линейной) системе дифференциальных уравнений, называемых уравнениями Максвелла:

(1.75)

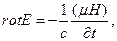(1.76)

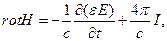(1.77)

где с = 3 • 10¹⁰ см/с — скорость света в пустоте.

Уравнение (1.76) выражает закон Фарадея, а уравнение (1.77) — закон Ампера.

Частные случаи уравнения Максвелла

а) r = 0, e = const, m = const и I = lЕ (закон Ома), l = const. Применяя к уравнениям (1.76) и (1.77) оператор rot и пользуясь уравнениями (1.75) для компонент векторов Е и Н получим так называемое телеграфное уравнение:

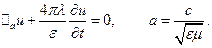(1.78)

б) I = 0, e = const, m= const. Вводя четырехкомпонентный элек­тромагнитный потенциал(A₀, А), A(x,t) = (A₁, A₂, A₃) представим решение уравнений Максвелла в виде:

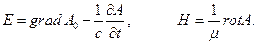(1.79)

При этом компоненты электромагнитного потенциала должны удов­летворять волновым уравнениям:

(1.80)

и условию Лоренца

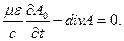
в) Если процесс стационарный, то уравнения Максвелла пре­вращаются в уравнения электростатики:

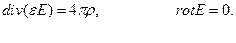
и в уравнения магнитостатики:

При e = const электростатический потенциал A₀ удовлетворяет (в си­лу (1.80)) уравнению Пуассона (1.66) с .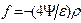

При преобразовании уравнения Максвелла мы пользовались следующими формулами векторного анализа:

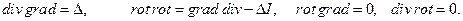
6. Уравнение Шрёдингера. Последним уравнение, которое будет приведено в наших методических указаниях, будет уравнение Шредингера. В данном курсе не будут рассматриваться задачи, связанные с квантовой механикой, однако, некоторыми ее результатами (например, значением ширины запрещенной зоны для полупроводниковых лазеров) мы будем пользоваться в дальнейшем. Поэтому рассмотрим основные допуски, заложенные при решении этого уравнения.

Пусть квантовая частица мас­сы m₀ движется во внешнем силовом поле с потенциалом V(x). Обозначим через ψ(х, t) волновую функцию этой частицы, так что |ψ(х, t) |²Δx есть вероятность того, что частица будет находиться в окрестности v(x) точки х вмомент времени t; здесь — Δ объем v(x). Тогда функция Ψ удовлетворяет уравнению Шрёдингера

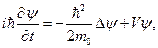(1.81)

где 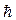= 1,054 • 10^-27эрг • с — постоянная Планка.

Если энергия Е частицы имеет определенное значение, то такое состояние ее называется стационарным. В этом случае волновая функция ψ(х, t) имеет вид

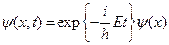
где волновая волна функция ψ(х,) в силу (1.81) удовлетворяет стационарному уравнению Шрёдингера

(1.82)

При V = 0 (свободная частица) уравнение Шрёдингера (1.82) превращается в однородное уравнение Гельмгольца (1.68).

Как и для уравнения Гельмгольца, в задачах на рассеяние на потенциале V необходимо требовать выполнения условий излучения Зоммерфельда (1.70) на бесконечности (где 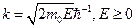).