Так как по условию дефект треугольника АВС равен нулю, то
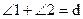 (12)
(12)
Так как точки А и Р симметричны относительно середины гипотенузы М, то
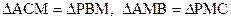
Докажите эти равенства самостоятельно). Отсюда следует, что , и . В силу равенства (12) . Аналогично, . Прямая ВР перпендикулярна АВ, а прямая РС перпендикулярна АС. Треугольники АВР и АСР – прямоугольные. По построению точки А и В1 центрально симметричны относительно точки В, следовательно они симметричны относительно прямой РВ. Отсюда следует, что
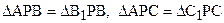 , (13)
, (13)
И треугольники ВРВ1 и СРС1 также прямоугольные. Из равенств треугольников (13) вытекает, что , и . Таким образом, в силу равенства (11), . Угол С1РВ1 – развернутый, точки С1, Р и В1 лежат на одной прямой. Из равенств (13) также следует, что и . Мы построили прямоугольный треугольник АВ1С1, стороны которого в два раза больше сторон исходного треугольника АВС, дефект которого равен 0 (см. (11)). Ясно, что, продолжая этот процесс, мы можем построить такой прямоугольный треугольник , для которого и .
Рассмотрим теперь произвольный прямоугольный треугольник RST с прямым углом 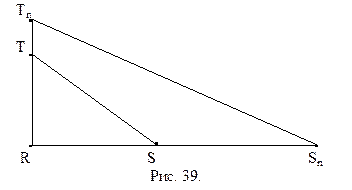 R. Выберем такое натуральное число n, чтобы катеты RS и RT удовлетворяли неравенствам:
R. Выберем такое натуральное число n, чтобы катеты RS и RT удовлетворяли неравенствам:
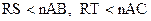 ,
,
где АВ и АС – катеты данного прямоугольного треугольника. Построим указанным выше способом прямоугольный треугольник 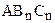 , у которого
, у которого 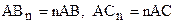 ,
, 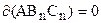 . Отложим на лучах RS и RT соответственно отрезки
. Отложим на лучах RS и RT соответственно отрезки 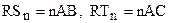 (рис. 39). Получим прямоугольный треугольник
(рис. 39). Получим прямоугольный треугольник 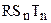 , равный
, равный 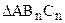 . По построению треугольник
. По построению треугольник 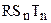 имеет нулевой дефект и, в силу свойства 10.6, дефект треугольника RST равен нулю. Лемма доказана.
имеет нулевой дефект и, в силу свойства 10.6, дефект треугольника RST равен нулю. Лемма доказана.
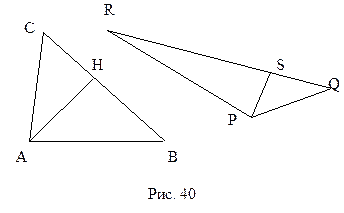 Как мы видим, лемма 10.8 представляет собой частный случай второй теоремы Лежандра. С ее помощью легко доказать это утверждение в общем случае. Предварительно сделаем следующее замечание. Если дан не прямоугольный треугольник, то его всегда можно разбить на два прямоугольных треугольника. Для этого достаточно провести высоту к его большей стороне, которая будет лежать внутри треугольника. Доказательство этого факта проведите самостоятельно.
Как мы видим, лемма 10.8 представляет собой частный случай второй теоремы Лежандра. С ее помощью легко доказать это утверждение в общем случае. Предварительно сделаем следующее замечание. Если дан не прямоугольный треугольник, то его всегда можно разбить на два прямоугольных треугольника. Для этого достаточно провести высоту к его большей стороне, которая будет лежать внутри треугольника. Доказательство этого факта проведите самостоятельно.
Пусть на плоскости дан произвольный треугольник АВС, дефект которого равен нулю. Рассмотрим второй произвольный треугольник PQR. Разобьем их соответственно на прямоугольные треугольники ACH, AHB и PSR, PSQ (рис. 40). Так как 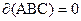 , то из свойства 10.5 следует, что дефекты прямоугольных треугольников AHB и AHC также раны нулю. Из леммы 10.8 вытекает, что дефект любого другого прямоугольного треугольника совпадает с нулем. Следовательно,
, то из свойства 10.5 следует, что дефекты прямоугольных треугольников AHB и AHC также раны нулю. Из леммы 10.8 вытекает, что дефект любого другого прямоугольного треугольника совпадает с нулем. Следовательно,
.
