Задача 4 к экзаменационным билетам по геометрии. 7 класс
Билет 1
1. Определение равнобедренного треугольника. Свойство углов при основании равнобедренного треугольника.
2. Найдите величины смежных углов, если один из них в 5 раз больше другого.
3. Определите, верно ли утверждение. ( Ответы да или нет)
1) Сумма углов любого треугольника равна 180°.
2) В равнобедренном треугольнике углы при основании тупые.
3) При пересечении двух параллельных прямых секущей накрест лежащие углы равны
Билет 2
1. Определение смежных углов. Свойство смежных углов.
2. Отрезки MN и DK пересекаются в их общей середине B. Докажите равенство треугольников MDB и NKB.
3. Определите, верно ли утверждение. ( Ответы да или нет)
1) При пересечении двух параллельных прямых секущей сумма односторонних углов равна 180°.
2) Внешний угол треугольника равен разности двух углов треугольника, не смежных с ним.
3) Если в треугольнике АВС углы А и В равны соответственно 40° и 70°, то и внешний угол при вершине С этого треугольника равен 70°.
Билет 3
1. Определение вертикальных углов. Свойство вертикальных углов.
2. Найдите периметр равнобедренного треугольника ADC с основанием AD, если AD = 7 см, DC = 8 см.
3. Определите, верно ли утверждение. ( Ответы да или нет)
1) Диагонали квадрата взаимно перпендикулярны.
2) Диагонали прямоугольника делят углы прямоугольника пополам.
3) Медиана треугольника делит стороны треугольника в отношении 2:1, считая от вершины.
Билет 4
1. Определение равных треугольников. Признаки равенства треугольников (доказательство одного из признаков по выбору учащегося).
2. Найдите неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 126° .
3. Определите, верно ли утверждение. ( Ответы да или нет)
1) Сумма острых углов треугольника равна 90°
2) Если гипотенуза одного прямоугольного треугольника равна гипотенузе другого треугольника, то такие треугольники равны.
3) Если две прямые перпендикулярны третьей, то они параллельны.
Билет 5
1. Определение медианы треугольника. Свойство медианы равнобедренного треугольника.
2. Точки М, N и R лежат на одной прямой, MN = 11 см, RN = 20 см. Найдите расстояние MR.
3. Определите, верно ли утверждение. ( Ответы да или нет)
1) Если один из вертикальных углов равен 80°, то другой так же равен 80°.
2) Сумма острых углов прямоугольного треугольника равна 90°.
3) Если два угла с общей вершиной равны, то они вертикальные.
Билет 6
1. Определение параллельных прямых. Признаки параллельности прямых (доказательство одного из признаков по выбору учащегося).
2. Угол, противолежащий основанию равнобедренного треугольника, равен 50° . Найдите величину внешнего угла при основании.
3. Определите, верно ли утверждение. ( Ответы да или нет)
1) Если две стороны и угол одного треугольника равны двум сторонам и углу другого треугольника, то такие треугольники равны.
2) Медиана прямоугольного треугольника является его высотой
3) Если один из смежных углов острый, то другой угол тупой.
Билет 7
1. Аксиома параллельных. Теоремы об углах, образованных двумя параллельными прямыми и секущей. (Доказательство одной из теорем по выбору учащегося.)
2. Найдите углы треугольника, на которые высота разбивает равносторонний треугольник.
3. Определите, верно ли утверждение. ( Ответы да или нет)
1) Катет прямоугольного треугольника лежащий напротив угла в 30°, равен половине гипотенузы
2) Медиана равностороннего треугольника является его высотой
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
Билет 8
1. Определение треугольника. Теорема о сумме углов треугольника.
2. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них равен 42° .
3. Определите, верно ли утверждение. ( Ответы да или нет)
1) Угол между биссектрисами вертикальных углов равен 180°.
2) Если две стороны одного треугольника равны двум сторонам другого треугольника, то такие треугольники равны
3) Если угол равен 50°, то смежный с ним угол тоже равен 50°.
Билет 9
1. Определение внешнего угла. Свойство внешнего угла.
2. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них 126° .
3. Определите, верно ли утверждение. ( Ответы да или нет)
1) Любой внешний угол треугольника больше каждого внутреннего угла этого треугольника
2) В треугольнике против меньшего угла лежит меньшая сторона
3) В треугольнике ABC, со сторонами AB=8, BC=6, AC=4, угол A является наибольшим
Билет 10
1. Определение прямоугольного треугольника. Свойство катета, лежащего напротив угла в 30° .
2. Найдите смежные углы, если один из них на 55° больше другого.
3. Определите, верно ли утверждение. ( Ответы да или нет)
1) Если два угла треугольника острые, то третий угол этого треугольника тупой
2) Треугольник со сторонами 1,2,3 не существует
3) Если катеты одного прямоугольного треугольника равны катетам другого треугольника, то такие треугольники равны.
Билет 11
1. Соотношение между сторонами и углами в треугольнике.
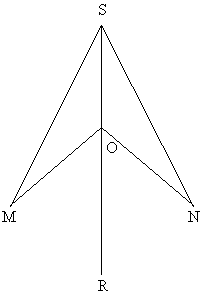
2. Луч SR является биссектрисой угла S, а отрезки SM и SN равны. Докажите равенство треугольников SMO и SNO.
3. Определите, верно ли утверждение. ( Ответы да или нет)
1) Любые две прямые имеют не менее одной общей точки
2) Если угол равен 900, то смежный с ним угол также равен 900
3) Через любые две точки проходит только одна прямая
Билет 12
1. Равнобедренный треугольник. Признак равнобедренного треугольника.
2. Найдите длину отрезка AM и градусную меру угла ABK, если BM – медиана, а BK – биссектриса треугольника ABC и известно, что AC = 17 см, угол ABC равен 84°
3. Определите, верно ли утверждение. ( Ответы да или нет)
1) Биссектрисы треугольника пересекаются в одной точке.
2) Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
3) Через любую точку проходит более одной прямой
Задача 4 к экзаменационным билетам по геометрии. 7 класс
(выдается на экзамене для оценки 5)
Билет 1
Докажите равенство отрезков, соединяющих середину основания равнобедренного треугольника с серединами боковых сторон.
Билет 2
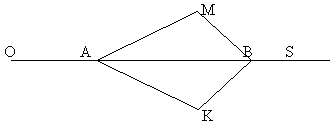
Известно, что 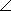 OAM =
OAM = 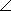 OAK и
OAK и 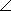 MBS =
MBS =  KBS. Докажите, что AK = AM, BM = BK.
KBS. Докажите, что AK = AM, BM = BK.
Билет 3
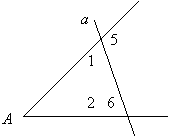
Прямая а пересекает стороны угла A. Докажите ,что  1 =
1 =  2, если известно, что
2, если известно, что 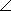 5 =
5 = 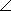 6.
6.
Билет 4
Отрезки AB и CM пересекаются в точке O. Луч OK является биссектрисой угла MOB. Найдите угол MOK, если угол AOM равен 86° .
Билет 5
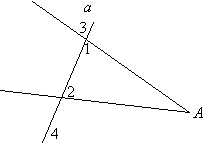
Прямая а пересекает стороны угла А. Докажите, что 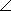 1 =
1 = 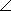 2, если известно, что
2, если известно, что 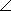 3 =
3 = 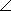 4.
4.
Билет 6
Найдите углы при основании MP равнобедренного треугольника МОР, если MK – его биссектриса и  OKM = 96°.
OKM = 96°.
Билет 7
В треугольнике MOK  O = 76°, а угол M в 3 раза меньше внешнего угла при вершине K. Найдите неизвестные углы треугольника.
O = 76°, а угол M в 3 раза меньше внешнего угла при вершине K. Найдите неизвестные углы треугольника.
Билет 8
Отрезки AB и CM параллельны и равны. Докажите, что AM = BC.
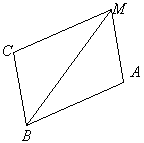
Билет 9
Докажите, что AB = CM.
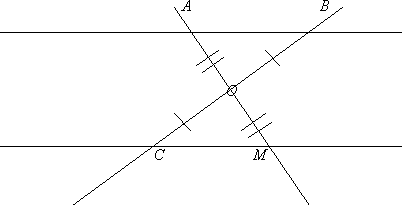
Билет 10
Треугольник MCB – равносторонний, BK и MP – его медианы, пересекающиеся в точке O.
Докажите равенство треугольников BOP и MOK.
Билет 11
Прямая, пересекающая основание равнобедренного треугольника, параллельна одной из боковых сторон. Докажите, что она отсекает равнобедренный треугольник.
Билет 12
В треугольниках BCK и B1C1K1CM и С1M1 – биссектрисы, CM = C1M1, углы BCK и B1C1K1 равны, углы CMK иC1M1K1 тоже равны. Докажите равенство треугольников BCK и B1C1K1.
