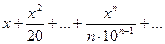Обчислення визначених інтегралів за допомогою формул прямокутників

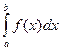При обчисленні інтегралу за формулами прямокутників підінтегральна функція 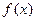заміняється «ступінчатою функцією», яка на кожному з відрізків 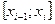має стале значення, рівне значенню функції 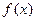на одному з кінців цього відрізка.

Нехай, наприклад, на кожному з відрізків 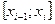ступінчата функція приймає значення, рівні значенню функції 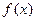на лівому кінці цього відрізку, тобто рівні 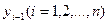. Тоді площа криволінійної трапеції 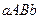(а відповідно, і значення шуканого інтеграла) вважається наближено рівній сумі площ прямокутників з висотами 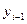і основами :

.

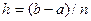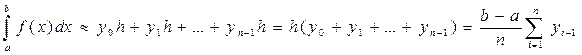Отже,

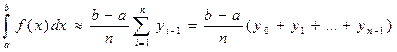. (1)

Якщо ж значення ступінчатої функції на кожному з відрізків 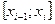співпадають зі значеннями функції 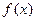на правих кінцях цих відрізків, то отримаємо формулу:

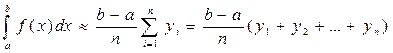. (2)

Формули (1) і (2) називаються формулами прямокутників.

Приклад:

Обчисліть 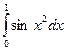за формулами прямокутників.

Розділимо відрізок 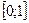на 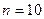частин. Тоді 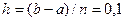. Складаємо таблицю значень підінтегральної функції.

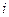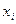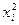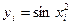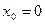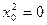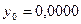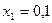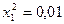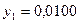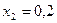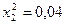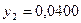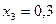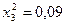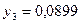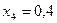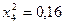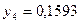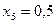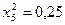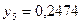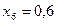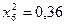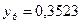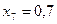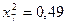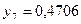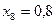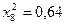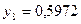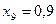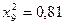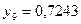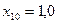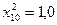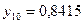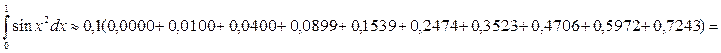За формулою прямокутників (1) отримаємо:

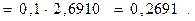
За формулою прямокутників (2) отримаємо:

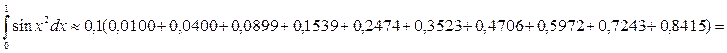
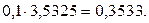
Обчислення визначених інтегралів за допомогою формул трапецій

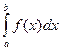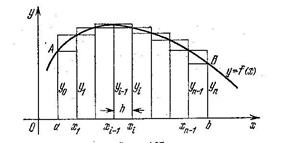
При обчисленні інтегралу за допомогою формули трапецій підінтегральна функція 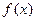замінюється функцією, графік якої представляє собою ламану лінію, ланки якої з’єднують кінці ординат 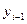і .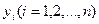

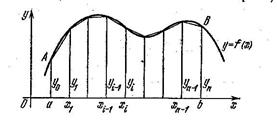
В цьому випадку площа криволінійної трапеції 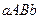(а, відповідно, і значення шуканого інтеграла) юбчислюється наближено рівній сумі площ звичайних трапецій з основами 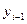і 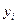і висотою :

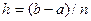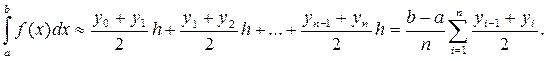
Отже,

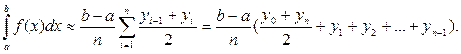(3)

Формула (3) називається формулою трапецій.

Приклад:

Обчисліть 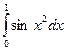за формулою трапецій.

Розділимо відрізок 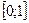на 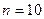частин. Тоді 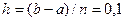. Складаємо таблицю значень підінтегральної функції.

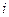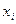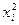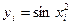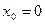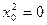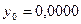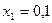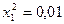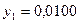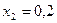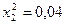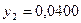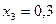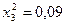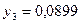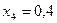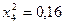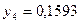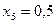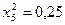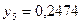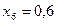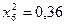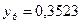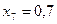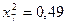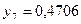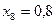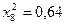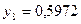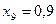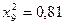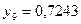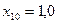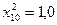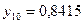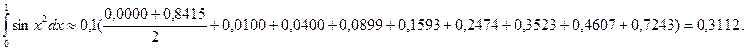За формулою трапецій (3) отримаємо:

Завдання самостійної роботи

1. Обчисліть за формулами прямокутників наближене значення інтегралу:

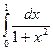при 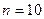з двома десятковими знаками.

1. Обчисліть за формулою трапеції наближене значення інтегралу:

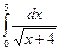при 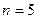з чотирма десятковими знаками.

Індивідуальні семестрові завдання

Обчислити площу фігури, обмеженої лініями.

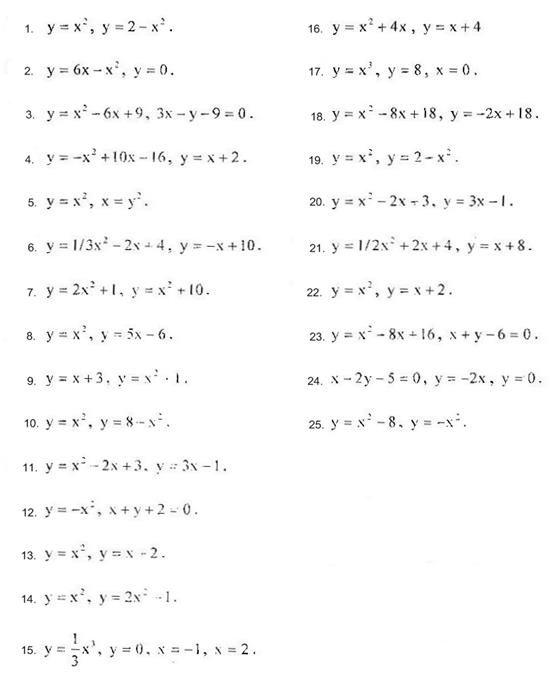
ЗАВДАННЯ САМОСТІЙНОЇ РОБОТИ .

Знайти подвійні інтеграли.

1. , .

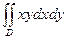
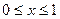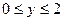2. , .

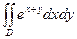
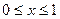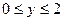Тема 4. РЯДИ. ( 14 ГОД. )

План .

1. Властивості збіжних рядів .

2. Ряд геометричноЇ прогресіЇ та гармонічний ряд .

3. Розв’язування завдань на знаходження області збіжності степеневих рядів.

4. Ряд Тейлора . Ряд Маклорена .

5. Розклад елементарних функцій у ряд Маклорена .

6. Застосування формули Тейлора для наближених обчислень.

Література. Барковський В.В. ,Барковська Н. В. Математика для економістів . Вища

математика.

ЗАВДАННЯ САМОСТІЙНОї РОБОТИ

Знайти область збіжності степеневих рядів

1.

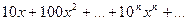
2.