Вывод уравнения молекулярно-кинетической теории идеальных газов для давления и его сравнения с уравнением Клайперона-Менделеева.

Основное уравнение молекулярно-кинетической теории идеального газа

Это уравнение связывает макропараметры системы – давление p и концентрацию молекул 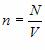с ее микропараметрами – массой молекул, их средним квадратом скорости или средней кинетической энергией:

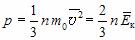
Вывод этого уравнения основан на представлениях о том, что молекулы идеального газа подчиняются законам классической механики, а давление – это отношение усредненной по времени силы, с которой молекулы бьют по стенке, к площади стенки.

Пропорциональность силы, с которой молекулы воздействуют на стенку, их концентрации, массе и скорости каждой молекулы качественно понятны. Квадратичный рост давления со скоростью связан с тем, что от скорости зависит не только сила отдельного удара, но и частота соударений молекул со стенкой.

Учитывая связь между концентрацией молекул в газе и его плотностью ( = nm₀), можно получить еще одну форму основного уравнения МКТ идеального газа:

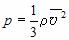
Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа)

В результате экспериментальных исследований многих ученых было установлено, что макропараметры реальных газов не могут изменяться независимо. Они связаны уравнением состояния:

pV = vRT

где R = 8,31 Дж/(K·моль) – универсальная газовая постоянная, 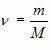, где m – масса газа и M – молярная масса газа. Уравнение Менделеева – Клапейрона называют уравнением состояния, поскольку оно связывает функциональной зависимостью параметры состояния. Его записывают и в других видах:

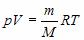
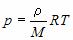
Пользуясь уравнением состояния, можно выразить один параметр через другой и построить график первого из них, как функции второго.

Графики зависимости одного параметра от другого, построенные при фиксированных температуре, объеме и давлении, называют соответственно изотермой, изохорой и изобарой.

Например, зависимость давления p от температуры T при постоянном объеме V и постоянной массе m газа – это функция 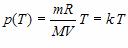, где k – постоянный числовой множитель. Графиком такой функции в координатах p,Т будет прямая, идущая от начала координат, как и графиком функции y(x)=kx в координатах y,x (рис. 3).

Зависимость давления p от объема V при постоянной массе m газа и температуре T выражается так:

,

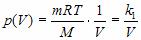где k₁ – постоянный числовой множитель. График функции 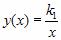в координатах y,x представляет собой гиперболу, так же как и график функции 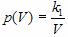в координатах p,V.

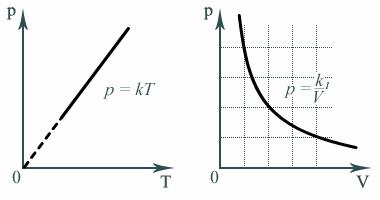
Рис. 3

Средняя кинетическая энергия молекул. Молекулярно-кинетическое толкование абсолютной температуры. Число степеней свободы. Закон равномерного распределения энергии по степеням свободы молекул.

Температура, как мера средней кинетической энергии молекул

Попробуем получить нетривиальные результаты, используя уравнение Клайперона-Менделеева и основное уравнение МКТ.

Введем понятие средней кинетической энергии молекул:

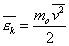(1)

Преобразуем основное уравнение МКТ с учетом формулы (1):

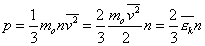т.е. основное уравнение МКТ запишем так 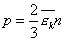(2)

Воспользуемся уравнением К.-М. в таком виде:

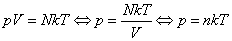(3)

Сравним уравнения (2) и (3) и получим, что

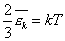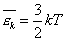или (4)

Как понимать формулу (4)?

Мы выяснили, что от температуры зависит величина средней кинетической энергии молекул. Поэтому говорят, что температура - мера средней кинетической энергии молекул. Это утверждение мы доказали на для идеального газа, но оказывается оно справедливо и для других агрегатных сосятояний вещества.

Молекулярно – кинетическое толкование абсолютной температуры.

C точки зрения молекулярно-кинетической теории молекулы нагретого тела находятся в хаотическом движении. Причем, чем выше температура T, тем больше средняя кинетическая энергия <ε_k>хаотического движения молекул (T~<ε_k>).

Связь между средней кинетической энергией поступательного движения молекулы и абсолютной температурой дается формулой <ε_k>=3/2kT где k - постоянная Больцмана, k=1.38*10^-23 (Дж/К). Следовательно, абсолютная температура есть мера средней кинетической энергии поступательного движения молекулы.

Формула позволяет выяснить смысл абсолютного нуля: T=0, если < ε_k > =0. Т. е. абсолютный нуль - это температура, при которой прекращается всякое хаотическое движение молекул.

Число степени свободы молекул. Закон равномерного распространения энергии по степеням свободы молекул.

Числом степеней свободы механической системы называется число независимых координат, полностью определяющих положение системы в пространстве.

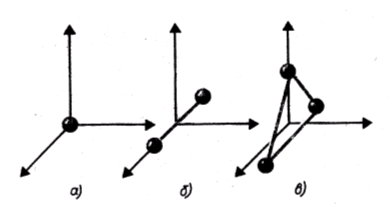показаны о дноатомная, двухатомная и трехатомная молекулы. Одноатомную молекулу можно представить как материальную точку. Для определения положения точки в пространстве нужно три координаты, т. е. три степени свободы поступательного движения (i = 3). Молекулу двухатомного газа в первом приближении можно рассматривать как совокупность двух жестко связанных материальных точек. Эта молекула кроме трех степеней свободы поступательного движения имеет две степени свободы вращательного движения (i = 5). Вращение вокруг оси, проходящей через оба атома, не учитывается.

Трехатомная молекула с жесткими связями имеет 6 степеней свободы: 3 - поступательного и 3 - вращательного движения (i = 6).

В классической физике принят постулат о равномерном распределении энергии по степеням свободы. На каждую степень свободы любого вида движения приходится энергия, равная kT/2. Таким образом, средняя энергия одной молекулы равна <ε₁>=i/2kT В классической физике принят постулат о равномерном распределении энергии по степеням свободы. На каждую степень свободы любого вида движения приходится энергия, равная kT/2. Таким образом, средняя энергия одной молекулы равна <ε₁>=i/2kT

закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы - в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией потому, что на нее приходится не только кинетическая энергия, но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы. Таким образом, средняя энергия молекулы <ε>=i/2kT, где i - сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы: i=i_пост +i_вращ+2i_колеб.

В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы.

Так как в идеальном газе взаимная потенциальная энергия молекул равна нулю, то внутренняя энергия, отнесенная к одному молю газа, равна сумме кинетических энергий NA молекул: 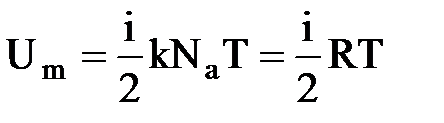.Внутренняя энергия для произвольной массы m газа 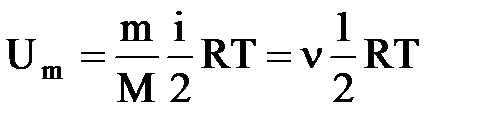, где k - постоянная Больцмана,  -количество вещества.

Функция распределения Максвелла – Больцмана характеризует распределение молекул по полным энергиям

38.Работа газа при изменении его объёма. Количество теплоты. Теплоёмкость. Первое начало термодинамики.

Работа газа при изменении его объёма. Одним из основных термодинамических процессов, совершающихся в большинстве тепловых машин, является процесс расширения газа с совершением работы. Легко определить работу, совершаемую при изобарном расширении газа.

Если при изобарном расширении газа от объема V₁ до объема V₂ происходит перемещение поршня в цилиндре на расстояние l , то работа A', совершенная газом, равна

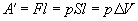
где p — давление газа, 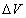— изменение его объема.

Количество теплоты — мера энергии, переходящей от одного тела к другому в данном процессе. Количество теплоты является одной из основных термодинамических величин.

Количество теплоты является функцией процесса, а не функцией состояния, то есть количество теплоты, полученное системой, зависит от способа, которым она была приведена в текущее состояние.

Q=cmΔt, где Q- полученная телом теплота, c- удельная теплоемкость тела, Дж/(кг°С), m- масса тела, кг, Δt-изменение температуры тела, °С

Теплоёмкость тела (обозначается C) — физическая величина, определяющая отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT:

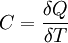
Единица измерения теплоёмкости в системе СИ — Дж/К.

Удельная теплоёмкость вещества — теплоёмкость единицы массы данного вещества. Единицы измерения — Дж/(кг К).

Молярная теплоёмкость вещества — теплоёмкость 1 моля данного вещества. Единицы измерения — Дж/(моль К).

Если же говорить про теплоёмкость произвольной системы, то ее уместно формулировать в терминах термодинамических потенциалов — теплоёмкость есть отношение малого приращения количества теплоты Q к малому изменению температуры T:

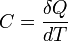
Первое начало термодинамики.

Первое начало термодинамики представляет собой обобщение опытных фактов и является по сути дела законом сохранения энергии, примененным к тепловым явлениям. Первое начало термодинамики имеет несколько формулировок. Одна из формулировок гласит: количество теплоты, переданное системе, идет на изменение внутренней энергии и на совершение системой работы над внешними телами, т. е. Q=∆U+A. В этом уравнении изменение внутренней энергии, Количество теплоты может быть положительным (Q>0), если тело получает теплоту, и отрицательным (Q>0), если тело отдает теплоту.

В дифференциальной форме это запишется следующим образом δQ=dU+δA

где dU и δA Первое начало термодинамики показывает, что теплоту можно преобразовывать в работу, т. е. выделять из неупорядоченного движения упорядоченное. Устройство, в котором теплота превращается в работу, называется тепловой машиной.

39.Приминение первого начала термодинамики к изопроцессам и адиабатному процессу идеального газа. Зависимость теплоёмкости идеального газа от вида процесса.

Первое начало термодинамики и изопроцессы.

Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным.

Изохорный процесс (V=const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат, где процесс 1-2 есть изохорное нагревание, а 1-3 - изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т.е.

.δA=pdV=0

Для изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии: Q=dU

DUm=CvdT. Тогда для произвольной массы газа получим Q=dU=mC_vT/M

Изобарный процесс (p=const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, параллельной оси V. При изобарном процессе работа газа при расширении объема от V1 до V2 равна

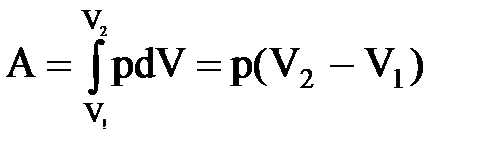и определяется площадью прямоугольника. Если использовать уравнение Клапейрона - Менделеева для выбранных нами двух состояний, то

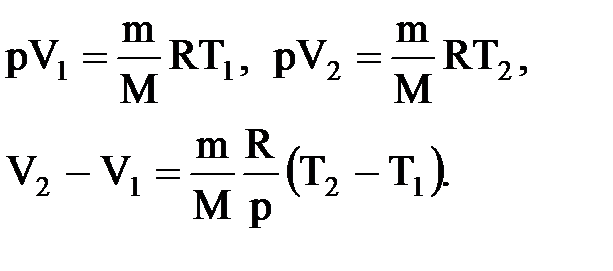
Тогда выражение для работы изобарного расширения примет вид

A=m/MR(T2-T1). Из этого выражения вытекает физический смысл молярной газовой постоянной R: если Т2-T1 =1 К, то для 1 моля газа R=А, т.е. R численно равна работе изобарного расширения 1 моля идеального газа при нагревании его на 1 К.

В изобарном процессе при сообщении газу массой m количества теплоты

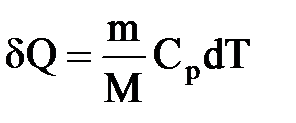его внутренняя энергия возрастает на величину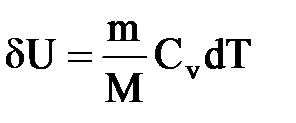

Изотермический процесс (T=const). Изотермический процесс описывается законом Бойля - Мариотта: PV=const.

Диаграмма этого процесса (изотерма)в координатах р, V представляет собой гиперболу, расположенную на диаграмме тем выше, чем выше температура, при которой происходил процесс. Работа изотермического расширения газа:

.

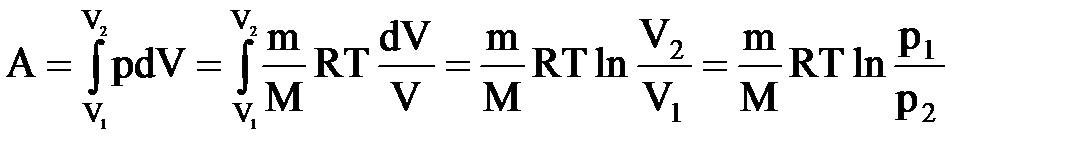Так как при T=const внутренняя энергия идеального газа не изменяется

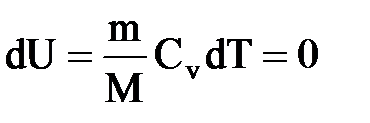то из первого начала термодинамики (Q=dU+A) следует, что для изотермического процесса Q=A, т.е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил 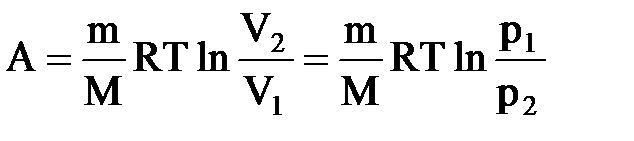Следовательно, для того, чтобы при работе расширения температура не уменьшалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.

Первое начало термодинамики и адиабатический процесс.

Адиабатическим называется процесс, при котором отсутствует теплообмен (dQ = 0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы. Адиабатические процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д. Из первого начала термодинамики d Q = dU + dA для адиабатического процесса следует, что d A = – dU * т. е. внешняя работа совершается за счет изменения внутренней энергии системы. Используя выражения для элементарной работы и приращения внутренней энергии, для произвольной массы газа получаем уравнение в виде pdV=-m/MC_vdT Продифференцировав уравнение состояния для идеального газа pV=m/MRT, получим pdV+Vdp=m/mRdT Исключив из уравнений температуру Т:

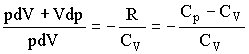
Разделив переменные и учитывая, что Cp/Cv = g , найдем dp/p=-γdV/V

Интегрируя это уравнение в пределах от р1 до р2 и соответственно от V1 до V2, а

затем потенцируя, придем к выражению p2/p1=(V₁/V₂) ^γ или p₁V₁^γ=p₂V₂^γ

Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

Для перехода к переменным Т, V или р, Т исключим из полученного уравнения с помощью уравнения Клапейрона -Менделеева

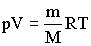соответственно давление или объем:TV^γ-1 = const T^γV^1-γ = const

Выражения представляют собой уравнения адиабатического процесса. В этих уравнениях 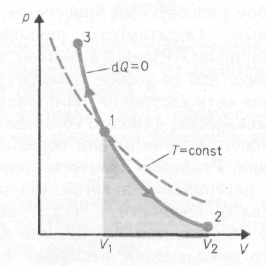безразмерная величина g = Cp/Cv = (i + 2)/I называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов (Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, i = 3, g = 1,67. Для двухатомных газов (Н2, N2, О2 и др.) i=5, g =1,4. Значения g , вычисленные по формуле (g = (i + 2)/i), хорошо подтверждаются экспериментом.

Диаграмма адиабатического процесса (адиабата) в координатах р, V изображается гиперболой. На рисунке видно, что адиабата (pVg = const) более крутая, чем изотерма (pV=const). Это объясняется тем, что при адиабатическом сжатии 1 - 3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры в адиабатическом процессе. Запишем уравнение первое начало термодинамик для адиабатического процесса dA = – dU в виде

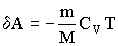Если газ адиабатически расширяется от объема Vl до V2, то его температура уменьшается от Т1 до Т2 и работа расширения идеального газа равна

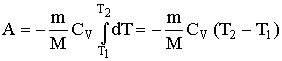
Работа, совершаемая газом при адиабатическом расширении 1 – 2 (численно равная площади под кривой), меньше, чем при изотермическом процессе. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом – температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.