Предмет и методы аналитической геометрии

Для успешных запусков космических аппаратов необходим точный расчет траекторий полета. Конструирование мостов и других сооружений происходит в строгом соответствии с результатами расчета геометрических параметров. В программировании для визуализации объектов необходимы знания для расчетов формы и траектории движения отдельных полигонов. В экономических задачах исследуют динамику и поведение рынка по графическим зависимостям и т.д.

Предметом аналитической геометрии является исследование форм геометрических образов и их взаиморасположение с помощью алгебры и анализа. Основные методы:

1. Метод координат; 2. Метод линейной геометрии.

Метод координат состоит в том, чтобы определить положение одного геометрического образа относительно другого с помощью чисел. С помощью метода координат каждой линии можно

поставить в соответствие уравнение . В аналитической геометрии на плоскости рассматриваются линии, описанные алгебраическими уравнениями 1-го порядка (прямая ) и алгебраическими уравнениями 2-го порядка (эллипс, окружность, гипербола, парабола ). С помощью метода координат каждой поверхности в пространстве можно поставить в соответствие уравнение .

Основные задачи аналитической геометрии

1. Дан геометрический образ (l или S) – составить уравнение.

2. По известному уравнению геометрического образа составить его вид.

2. Линейные пространства

Определение 1.

Числовым полем называется любое числовое множество, замкнутое относительно операций сложения, вычитания, умножения и деления (кроме деления на 0). Аналогичное определение можно дать для различных полей.

Определение 2.

Непустое множество элементов любой природы называется линейным пространством (L) на некотором поле, если оно удовлетворяет двум условиям

I. , : . Определена операция сложения, не выводящая за пределы L и обладающая определенными свойствами:

1) – свойство коммутативности (перестановки);

2) – свойство ассоциативности;

3) : – существование нулевого элемента;

4) : – существование отрицательных элементов.

II. , : . Возможна операция умножения на число, обладающая определенными свойствами:

1) , ;

2) – существование единичного элемента;

3) – дистрибутивное свойство;

4) – дистрибутивное свойство.

ПРИМЕР 1. Линейные пространства.

1. R – множество действительных чисел.

2. – n-мерное пр-во, множество упорядоченных наборов действительных чисел . В частности, – множество точек плоскости, 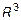– множество точек пространства.

3. – множество функций, непрерывных на 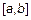. В частности, – пространство непрерывных сигналов ( ).

4. – множество функций квадратинтегрируемых на 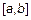, т. е. существует .

3. Нормированные пространства

Определение 3.

Отображение линейного пространства L на множество действительных чисел R называется функционалом .

Определение 4.

Нормой элемента называется функционал , удовлетворяющий условиям:

1) ;

2) ;

3) .

Норма элемента x обозначается значком ||x||. Пространство, в котором введена норма, называется нормированным.

ПРИМЕР 2.

1. Для R, .

2. Для , .

3. Для за норму принимают .

4. Для , норма ,

4. Векторы в пространстве

Скалярная величина – это численное значение.

Векторная величина определена не только численным значением, но и направлением.

Определение 5.

Вектором называется направленный отрезок прямой и обозначается или 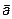, где A – начало вектора; В – конец вектора. ; модуль вектора – , , .

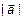Определение 6.

Два вектора называются коллинеарными, если они лежат на одной или на параллельных прямых, обозначаются . Если они направлены в одну сторону (сонаправленные), то записывают , а если в противоположные, то записывают .

Определение 7.

Два вектора равны , два вектора противоположны .

Определение 8.

Если векторы лежат на одной или параллельных плоскостях, то они называются компланарными (соплоскостными).

5. Линейные операции над векторами

5.1. Сложение векторов

Дано: . Найти: .

1. Правило треугольника (рис. 1а).

2. Правило параллелограмма (рис. 1в).

Если слагаемых векторов больше 2, правило треугольника обобщается правилом многоугольника (рис. 1б) .

5.2. Вычитание векторов

Т. к. , или . Следовательно, справедливо правило параллелограмма или треугольника. Вектор 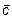имеет следующее направление: начало вектора совпадает с концом вычитаемого вектора, и конец вектора совпадает с началом вектора, из которого вычитают (рис. 2).

5.3. Умножение вектора на скаляр

Определение 9.

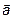Произведение вектора на скаляр называется вектор . Следствия: a) ; б) если , если ; в) Если , то .

Определение 10.

Вектор называется единичным вектором (рис. 3) вектора 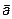, если ,

Заключение

В лекции определены роль и место высшей математики в современной науке; изучены предмет, методы и задачи аналитической геометрии, понятия линейного, нормированного пространств. Они важны для восприятия в дальнейшем известных со школы понятий и операций с точки зрения высшей математики. Обращалось внимание на часть школьного курса о векторах и операциях над ними, чтобы в дальнейшем систематизировать знания по векторной алгебре. Отметим следующее:

- математика – точный инструмент всех наук;

- линии описываются алгебраическими уравнениями 1-го порядка (прямая) и алгебраическими уравнениями 2-го порядка (эллипс, окружность, гипербола, парабола);

- норма в пространстве задается как длина вектора;

- существуют линейные пространства, они могут быть нормированными.

Литература

1. Бермант А.Ф. и др. Краткий курс математического анализа. – М.: Высшая школа, 2001.

2. Рыжков В. В. Лекции по аналитической геометрии. – М.: Факториал пресс, 2000, – 208 с.

3. Шнейдер В.Е. и др. Краткий курс высшей математики. – М.: Высшая школа, 1998.

4. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.

Лекция 6