Общее понятие эконометрических моделей. Виды эконометрических моделей
Моделью называется материальный или мысленно представляемый объект, замещающий в процессе исследования объект-оригинал таким образом, что его непосредственное изучение дает новые знания об объекте-оригинале. Модель выступает в качестве средства анализа и прогнозирования конкретных экономических процессов на основе реальной статистической информации. Применение метода моделирования вызвано тем, что большинство объектов (или проблем, относящихся к этим объектам) непосредственно исследовать или совершенно невозможно, или подобное исследование требует много времени и средств.
Главным инструментом эконометрического исследования является модель. Выделяют три основных класса эконометрических моделей:
1) модель временных рядов;
2) модели регрессии с одним уравнением;
3) системы одновременных уравнений.
Моделью временных рядов называется зависимость результативной переменной от переменной времени или переменных, относящихся к другим моментам времени.
К моделям временных рядов, характеризующих зависимость результативной переменной от времени, относятся:
а) модель зависимости результативной переменной от трендовой компоненты или модель тренда;
б) модель зависимости результативной переменной от сезонной компоненты или модель сезонности;
в) модель зависимости результативной переменной от трендовой и сезонной компонент или модель тренда и сезонности.
К моделям временных рядов, характеризующих зависимость результативной переменной от переменных, датированных другими моментами времени, относятся:
а) модели с распределённым лагом, объясняющие вариацию результативной переменной в зависимости от предыдущих значений факторных переменных;
б) модели авторегрессии, объясняющие вариацию результативной переменной в зависимости от предыдущих значений результативных переменных;
в) модели ожидания, объясняющие вариацию результативной переменной в зависимости от будущих значений факторных или результативных переменных.
Кроме рассмотренной классификации, модели временных рядов делятся на модели, построенные по стационарным и нестационарным временным рядам.
Стационарным временным рядом называется временной ряд, который характеризуется постоянными во времени средней, дисперсией и автокорреляцией, т. е. данный временной ряд не содержит трендовой и сезонной компонент.
Нестационарным временным рядом называется временной ряд, который содержит трендовую и сезонную компоненты.
Определение. Моделью регрессии с одним уравнением называется зависимость результативной переменной, обозначаемой как у, от факторных (независимых) переменных, обозначаемых какх1,х2,…,хn. Данную зависимость можно представить в виде функции регрессии или модели регрессии:
y=f(x,β)=f(х1,х2,…,хn, β1…βk)
где β1…βk – параметры модели регрессии.
Можно выделить две основных классификации моделей регрессии::
а) классификация моделей регрессии на парные и множественные регрессии в зависимости от числа факторных переменных;
б) классификация моделей регрессии на линейные и нелинейные регрессии в зависимости от вида функции f(x,β).
В качестве примеров моделей регрессии с одним уравнением можно привести следующие модели:
а) производственная функция вида Q=f(L,K), выражающая зависимость объёма производства определённого товара (Q) от производственных факторов – от затрат капитала (К) и затрат труда (L);
б) функция цены Р=f(Q,Pk), характеризующая зависимость цены определённого товара (Р) от объема поставки (Q) и от цен конкурирующих товаров (Pk);
в) функция спроса Qd=f(P,Pk,I), характеризующая зависимость величины спроса на определённый товар (Р) от цены данного товара (Р), от цен товаров-конкурентов (Pk) и от реальных доходов потребителей (I).
Системой одновременных уравнений называется модель, которая описывается системами взаимозависимых регрессионных уравнений.
Системы одновременных уравнений могут включать в себя тождества и регрессионные уравнения, в каждое из которых могут входить не только факторные переменные, но и результативные переменные из других уравнений системы.
Регрессионные уравнения, входящие в систему одновременных уравнений, называются поведенческими уравнениями. В поведенческих уравнениях значения параметров являются неизвестными и подлежат оцениванию.
Основное отличие тождеств от регрессионных уравнений заключается в том, что их вид и значения параметров известны заранее.
Примером системы одновременных уравнений является модель спроса и предложения, в которую входит три уравнения:
а) уравнение предложения: =а0+а1*Рt+a2*Pt-1;
б) уравнение спроса: =b0+b1* Рt+b2*It;
в) тождество равновесия: QSt = Qdt,
где QSt – предложение товара в момент времени t;
Qdt – спрос на товар в момент времени t;
Рt – цена товара в момент времени t;
Pt-1 – цена товара в предшествующий момент времени (t-1);
It– доход потребителей в момент времени.
В модели спроса и предложения выражаются две результативные переменные:
а) Qt– объём спроса, равный объёму предложения в момент времени t;
б) Pt– цена товара в момент времени t.
Регрессия – это приближение на основе правильной спецификации (в выборе вида приближения). Модели регрессии задаются на основе исходной реальной ситуации, за основу выбирается аддитивная лин зависимость.
В классической модели регрессии полагают, что найденные значения оценок а, b явл-ся наилучшими из возможных для параметров 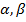 соответственно. Всегда полагают, что реальную действительность можно узнать только на шестом этапе эконометрического моделирования (верификация). Однако этого недостаточно в связи с ограничением на ресурсы, поэтому разработали качественный метод, к-ый позволяет построить модель, близкую к реальности.
соответственно. Всегда полагают, что реальную действительность можно узнать только на шестом этапе эконометрического моделирования (верификация). Однако этого недостаточно в связи с ограничением на ресурсы, поэтому разработали качественный метод, к-ый позволяет построить модель, близкую к реальности.
Модели регрессии исследуются с помощью методов наим квадратов, если выполняются условия Гаусса-Маркова, то исп-ся классический МНК.
Классческие модели регрессии подразделяют на два вида: лин и нелинейные – в зависимости от формы связи между переменными. Каждый из видов, в свою очередь, делится на парную и множественную модель.
В свою очередь, нелин модели подразделяются на два класса в зависимости от метода перехода к линейным (линеаризация).
К первому классу отн-ся модели лин по оцениваемым параметрам, но нелин по входящим переменным. Например:
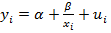 – НМ (1)
– НМ (1)
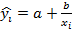 – НМР
– НМР
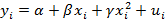 – НМ (2)
– НМ (2)
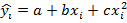
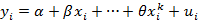 .
.
Второй класс моделей – нелин отн-но оцениваемых параметров. Например:
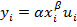 – НМ
– НМ
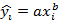 – НМР
– НМР
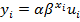 – НМ
– НМ
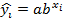 – НМР.
– НМР.
Классы распределились с учетом сложности алгебраических преобразований или обычных подстановок (замены).
Первый класс
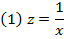
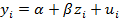
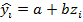
| i | x | y | z = 1/x |
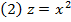
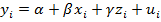
Осуществился переход к модели множественной регрессии в связи с добавлением нового фактора, так как формально новый фактор коррелирован со старым. На практике для целей управления и принятия решений никогда не берут полиномы степени больше трех.
| i | x | y | z = x2 |
При решении задач на ПК в моделях с полиномами следует размещать все данные по экзогенным переменным рядом.
| i | x | z = x2 | y |
Второй класс
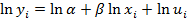
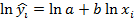
| i | x | y | lnx | lny |
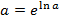
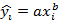
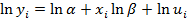
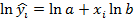
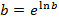
| i | x | y | lny |
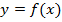
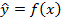
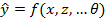
На практике подбор вида ф-ии осущ-ся несколькими способами:
1. Графическим;
2. Опытным путем.
