Достаточные признаки сходимости
Знакоположительных рядов
| Признак Даламбера. | Если для положительного ряда существует 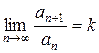 , то , то |
§ при 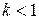 ряд сходится,
ряд сходится,
§ при 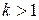 ряд расходится,
ряд расходится,
§ при 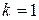 о сходимости ряда сказать ничего нельзя, т.е. надо применять другой признак.
о сходимости ряда сказать ничего нельзя, т.е. надо применять другой признак.
Пример. Исследовать на сходимость ряд
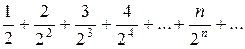
Решение. Находим 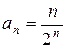 ,
, 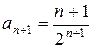 .
.
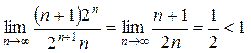 – ряд сходится.
– ряд сходится.
| Интегральный признак Коши. | Ряд с положительными членами 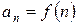 сходится или расходится одновременно с несобственным интегралом сходится или расходится одновременно с несобственным интегралом |
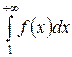 ,
,
где 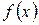 – непрерывная, положительная, монотонная убывающая производящая функция.
– непрерывная, положительная, монотонная убывающая производящая функция.
Пример. Исследовать на сходимость гарнмонический ряд 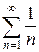 .
.
Решение. Вычислим
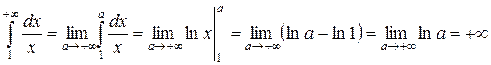 .
.
Гармонический ряд расходится.
Пример.Исследовать на сходимость ряд 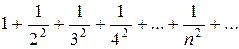
Решение. Члены ряда можно рассматривать как значения функции 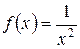 при
при 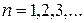 Члены ряда убывают:
Члены ряда убывают: 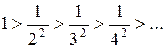 Вычислим
Вычислим
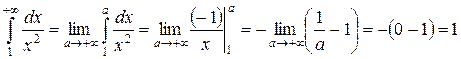 .
.
Несобственный интеграл сходится, значит сходится и данный ряд.
| Радикальный признак Коши. | Если для положительного ряда существует 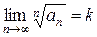 , то , то |
§ при 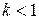 ряд сходится,
ряд сходится,
§ при 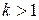 ряд расходится,
ряд расходится,
§ при 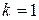 о сходимости ряда сказать ничего нельзя.
о сходимости ряда сказать ничего нельзя.
(Этот признак применяется лишь тогда, когда 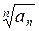 извлекается).
извлекается).
Пример. Исследовать на сходимость 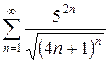
Решение. Преобразуем выражение под знаком суммы.
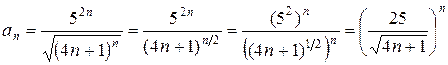
Применяя радикальный признак Коши, имеем:
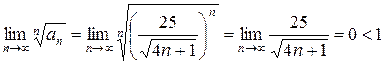
Таким образом, исходный ряд сходится.
| Первый признак сравнения. | Сравним ряд с положительными членами 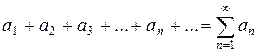 с другим знакоположительным рядом с другим знакоположительным рядом 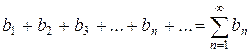 |
§ если ряд 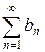 сходится и начиная с некоторого члена ряда выполняется неравенство
сходится и начиная с некоторого члена ряда выполняется неравенство 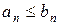 , то ряд
, то ряд 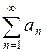 также сходится;
также сходится;
§ если ряд 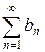 расходится и начиная с некоторого члена ряда выполняется неравенство
расходится и начиная с некоторого члена ряда выполняется неравенство 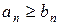 , то и ряд
, то и ряд 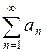 также расходится.
также расходится.
Пример. Исследовать сходимость ряда 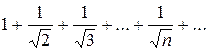
Решение. Сравним данный ряд с гармоническим рядом
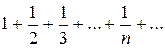
Т.к. каждый член исходного ряда, начиная со второго, больше соответствующего члена гармонического ряда, а гармонический ряд является расходящимся (интегральный признак), то данный ряд тоже расходится.
Замечание. Обобщенный гармонический ряд 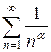 при
при 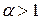 сходится, при
сходится, при 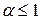 расходится.
расходится.
| Второй признак сравнения. | Даны два положительных ряда 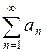 и и 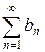 . Если существует конечный предел отношения членов ряда при . Если существует конечный предел отношения членов ряда при 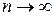 , отличный от нуля, то оба ряда сходятся, либо расходятся одновременно, т.е. , отличный от нуля, то оба ряда сходятся, либо расходятся одновременно, т.е. 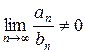 и и 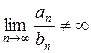 . . |
Пример. Исследовать ряд на сходимость 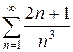 .
.
Решение. Сравним этот ряд со сходящимся рядом 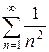 (он сходится по интегральному признаку). Проверим, существует конечный, отличный от нуля предел
(он сходится по интегральному признаку). Проверим, существует конечный, отличный от нуля предел
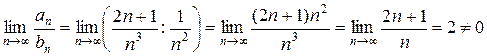 .
.
Таким образом, ряд является сходящимся.
Знакочередующиеся ряды
Ряд 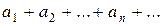 называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
Признак сходимости знакопеременного ряда.Если ряд 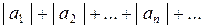 , составленный из абсолютных величин членов знакопеременного ряда, сходится, то и исходный ряд сходится.
, составленный из абсолютных величин членов знакопеременного ряда, сходится, то и исходный ряд сходится.
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин членов данного ряда.
Сходящийся знакопеременный ряд называется условно сходящимся, если ряд, составленный из абсолютных величин его членов, расходится.
Ряд вида
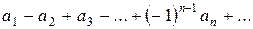 ,
,
где 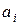 – положительные числа, называется знакочередующимся.
– положительные числа, называется знакочередующимся.
| Признак Лейбница. | Знакочередующийся ряд сходится, если его члены монотонно убывают по абсолютной величине и модуль общего члена стремится к нулю при 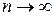 , т.е. , т.е. 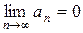 . . |
Пример. Исследовать на сходимость ряд 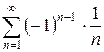 .
.
Решение. Находим: 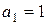 ,
, 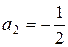 ,
, 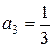 ,
, 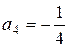 .
.
1) Члены ряда монотонно убывают по абсолютной величине: 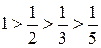 .
.
2) 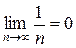 .
.
Условия сходимости знакочередующегося ряда выполняются, значит данный ряд сходится.
| 9. Степенные ряды |
Ряд 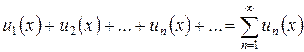 , членами которого являются функции от
, членами которого являются функции от 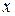 называется функциональным.
называется функциональным.
Функциональный ряд называется сходящимся в точке 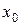 , если при
, если при 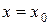 он обращается в сходящийся числовой ряд.
он обращается в сходящийся числовой ряд.
Функциональный ряд называется расходящимся в точке 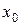 , если при
, если при 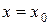 он обращается в расходящийся числовой ряд.
он обращается в расходящийся числовой ряд.
Множество значений 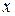 , при которых функциональный ряд сходится, называется областью сходимости функционального ряда.
, при которых функциональный ряд сходится, называется областью сходимости функционального ряда.
Функциональный ряд вида
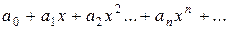
или
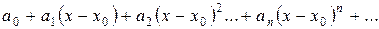 ,
,
где 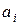 – числа, называемые коэффициентами, называется степеннымрядом.
– числа, называемые коэффициентами, называется степеннымрядом.
Ряд, который сходится при любом значении 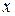 , называется всюдусходящимся.
, называется всюдусходящимся.
