Сводка и группировка данных статистического наблюдения
Министерство науки и образования РК
Евразийский Технологический Университет
РЕФЕРАТ
На тему: «Статистический анализ»
Выполнила: Самазбаева А.
Проверила: Иматаева А.
Алматы 2015 г.
Введение
Многие окружающие нас процессы можно выразить с помощью числовых значений. Однако этих чисел оказывается так много и они носят различный характер, что для обыденного человека не представляют никакой информации. Методы статистики позволяют анализировать такие данные, находить закономерности и даже строить прогнозы.
Основываясь на статистических данных, мы можем предсказывать развитие различных ситуаций. Что помогает нам как в технике, так и в управленческой деятельности при принятии различных решений. Именно поэтому знание основных методов статистики необходимо для того, чтобы успешно решать различного рода задачи.
Количество данных, поступающих к нам из внешнего мира, постоянно растет, поэтому статистические методы, применяемые для упорядочивания этих данных, представления их в удобном для рассмотрения и анализа виде, никогда не теряют своей актуальности.
Сводка и группировка данных статистического наблюдения
Выполним сводку по показателю «Площадь жилищ, приходящаяся в среднем на одного жителя, по регионам Российской Федерации, весь жилищный фонд; кв. м/чел.» на конец 2009 г.
Простая сводка по показателю «Площадь жилищ, приходящаяся в среднем на одного жителя, по регионам Российской Федерации, весь жилищный фонд» на конец 2009 г.
Проанализировав все данные можно выделить две республики, данные по которым значительно отличаются от всей совокупности. Вследствие этого, уберем из расчетов Чеченскую республику и республику Ингушетия.
Построим простую группировку, с выделением групп субъектов со значением показателя выше и ниже среднего по Российской Федерации.
Рассчитаем среднее по группе, расчет выполним как простую арифметическую величину по формуле (1):
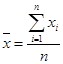 , кв. м/чел. (1)
, кв. м/чел. (1)
где n – число субъектов РФ в данной группе,
Xi – значение по каждому субъекту.
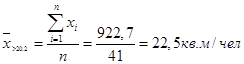
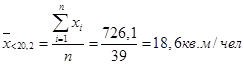
Результат занесем в таблицу 1.2.
Таблица 1.2 – Простая группировка с выделением групп субъектов выше и ниже среднего по Российской Федерации относительно среднего значения по России
| Площадь жилищ, кв. м/чел | Количество субъектов | В % к общему числу | Среднее по группе, кв. м/чел |
| Ниже среднего по РФ (< 20,2 кв. м/чел.) | 48,75 | 18,6 | |
| Выше среднего по РФ (> 20,2 кв. м/чел.) | 51,25 | 22,5 | |
| Итого | 100,00 | 20,2 |
Отобразим полученные результаты на графике, показанном на рисунке 1.1, для простой группировки лучшим образом подойдет круговая диаграмма.
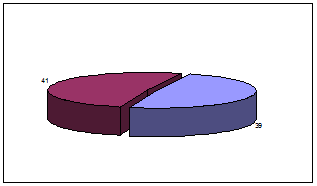
Рисунок 1.1 – Доля субъектов со значением выше и ниже среднего по Российской Федерации
Построим простую группировку, с выделением групп субъектов со значением показателя выше и ниже среднего относительно Челябинской области.
Рассчитаем среднее по группе, расчет выполним как простую арифметическую величину по формуле (1).
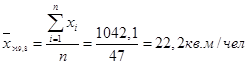
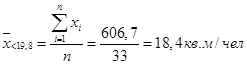
Результат занесем в таблицу 1.3.
Таблица 1.3 – Простая группировка с выделением групп субъектов выше и ниже среднего относительно Челябинской области
| Площадь жилищ, кв. м/чел | Количество субъектов | В% к общему числу | Среднее по группе, кв. м/чел. |
| Ниже среднего по ЧО (< 19,8 кв. м/чел.) | 41,25 | 18,4 | |
| Выше среднего по ЧО (> 19,8 кв. м/чел.) | 58,75 | 22,2 | |
| Итого | 100,00 | 20,2 |
Отобразим полученные результаты на графике, показанном на рисунке 1.2. Для простой группировки лучшим образом подойдет круговая диаграмма.
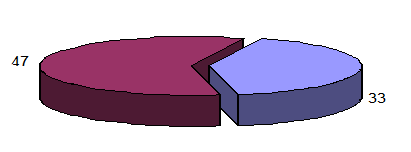
Рисунок 1.2 – Доля субъектов со значением выше и ниже среднего по Челябинской области
Выполнив простые группировки видно, что в среднем значение показателя по РФ не сильно варьируется. Это обусловлено тем, что в каждом субъекте соотношение жителей и жилой площади сопоставимо. Поэтому разброс значений показателя не велик.
Вариационный анализ
Выполним вариационный анализ показателя «Площадь жилищ, приходящаяся в среднем на одного жителя, по регионам Российской Федерации, весь жилищный фонд» на конец 2009 г.
Для этого построим вариационный ряд. Так как признак непрерывный, то необходимо разбить все значения на интервалы. Количество интервалов примерно можно определить с помощью формулы Стержесса:
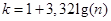 (2)
(2)
где k – количество интервалов,
n – количество субъектов РФ, попадающих в вариационный анализ.
Длину интервалов считаем по формуле (3):
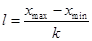 , кв. м/чел. (3)
, кв. м/чел. (3)
Подставим значения и посчитаем количество интервалов и шаг интервалов.
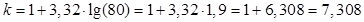
Примем k = 8.
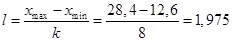 кв. м/чел.
кв. м/чел.
Так как в вариационном ряду встречаются максимальные и минимальные значения отличные от общей вариации, посчитаем другую длину интервала.
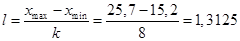 кв. м/чел.
кв. м/чел.
Примем длину интервала l = 1,5 кв. м/чел.
Исходя из полученных интервалов и длины построим таблицу 2.1
Отобразим вариационный ряд графически. Для отображения вариационного ряда наиболее подходящим графиком является гистограмма. Построим гистограмму рисунок 2.1 по полученным значениям.
Таблица 2.1 – Распределение количества субъектов РФ
| Площадь жилищ, кв. м/чел | Количество субъектов |
| < 15,0 | |
| 15,0 – 16,5 | |
| 16,5 – 18,0 | |
| 18,0 – 19,5 | |
| 19,5 – 21,0 | |
| 21,0 – 22,5 | |
| 22,5 – 24,0 | |
| > 24,0 | |
| Итого |
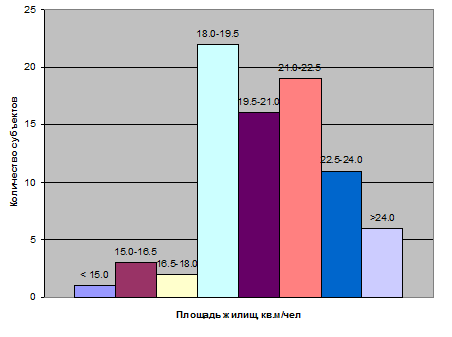
Рисунок 2.1 – Гистограмма распределения числа субъектов РФ в зависимости от площади жилищ, приходящейся на одного жителя
Построим кумуляту и огиву на рисунке 2.2, для этого составим таблицу 2.2 накопленных частот для кумуляты и огивы.
Таблица 2.2 – Накопленные значения для кумуляты и огивы
| Площадь жилищ, кв. м/чел | Количество субъектов | Накопленные частоты для кумуляты | Накопленные частоты для огивы |
| < 15,0 | |||
| 15,0 – 16,5 | |||
| 16,5 – 18,0 | |||
| 18,0 – 19,5 | |||
| 19,5 – 21,0 | |||
| 21,0 – 22,5 | |||
| 22,5 – 24,0 | |||
| > 24,0 | |||
| Итого | - | - |
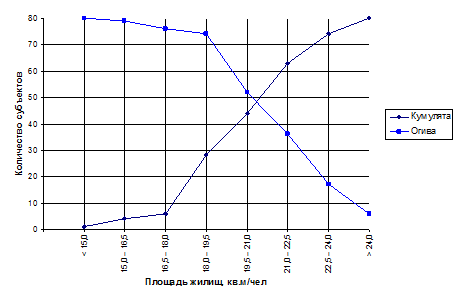
Рисунок 2.2 – Кумулята и огива распределения количества субъектов
Выполним расчет числовых характеристик показателя.
Необходимо рассчитать среднее значение вариационного ряда. Для интервального ряда среднее значение ряда считается по формуле (4):
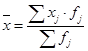 (4)
(4)
где xi – центр интервала,
fi – количество единиц в j-том интервале.
Подставим значения в формулу (4) и получим: 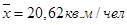
Для характеристики структуры вариационного ряда рассчитаем моду и медиану, они рассчитываются по формулам (5) и (6) соответственно:
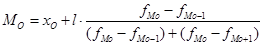 (5)
(5)
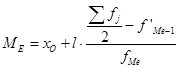 (6)
(6)
Подставим значения и получим:
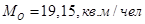 ,
, 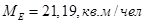
Оценим также силу и размах вариации, они рассчитываются по формулам (7), (8), (9):
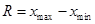 (7)
(7)
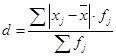 (8)
(8)
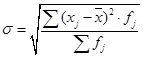 (9)
(9)
Подставим значения в формулы и получим:
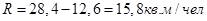
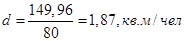
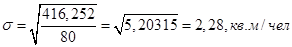
Посчитаем все остальные показатели по вариационному ряду.
– дисперсия: 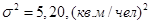
– относительный размах вариации: 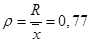
– относительное линейное отклонение: 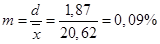
– коэффициент вариации: 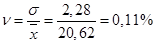
Также необходимо узнать распределение показателя по всему диапазону значений. Для этого вычислим показатели характера вариации:
– коэффициент асимметрии: 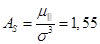
– показатель эксцесса: 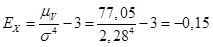
Для удобства и наглядности все полученные значения в ходе вычислений сведем в таблицу 2.3
Таблица 2.3 – Показатели вариации для распределения площади жилищ, приходящейся на одного жителя
| № п/п | Название показателя | Значение показателя |
| Среднее значение, кв. м/чел | 20,62 | |
| Мода, кв. м/чел | 19,15 | |
| Медиана, кв. м/чел | 21,19 | |
| Размах вариации, кв. м/чел | 15,8 | |
| Среднее линейное отклонение, кв. м/чел | 1,87 | |
| Среднее квадратическое отклонение, кв. м/чел | 2,28 | |
| Дисперсия, (кв. м/чел.)2 | 5,20 | |
| Относительный размах вариации | 0,77 | |
| Относительное линейное отклонение, % | 0,09 | |
| Коэффициент вариации, % | 0,11 | |
| Коэффициент асимметрии | 1,55 | |
| Эксцесс | – 0,15 |
Так как выполняется неравенство 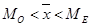 , то распределение не симметричное. Коэффициент асимметрии показывает, что существует значительная асимметрия.
, то распределение не симметричное. Коэффициент асимметрии показывает, что существует значительная асимметрия.
Отрицательный показатель эксцесса показывает, что разброс показателя достаточно велик. Цель вариационного анализа достигнута.
Выборочное наблюдение
Произведем отбор 27 и 35 субъектов из генеральной совокупности.
Будем производить случайный отбор субъектов РФ.
Составим две таблицы из 27 и 35 субъектов соответственно 3.1 и 3.2.
Посчитаем выборочные средние для двух выборок:
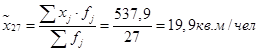
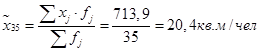
Найдем дисперсию для обеих выборок:
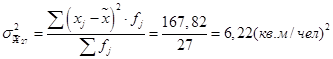
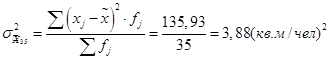
Для определения предельной ошибки возьмем вероятность попадания в интервал 0,99. По таблице в приложении 2, 3 страница 34–37 /1/, найдем значение коэффициента t = 2,58 и tСт=2,779. Подставим значения и посчитаем предельные ошибки для обоих случаев:
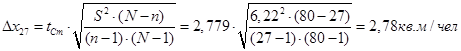
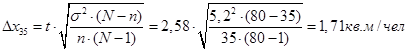
Таким образом, генеральная средняя будет лежать в пределах:
· при малой выборке: 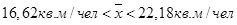
· при большой выборке: 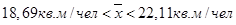
По заданию необходимо определить доверительный интервал генеральной средней по выборочным данным с вероятностью 0,689; 0,789; 0,889; 0,959. Для этого необходимо из таблиц приложений /1/ выписать соответствующие значения коэффициентов t и tСт. Подставим значения в формулы и посчитаем, а результаты занесем в таблицы 3.3 и 3.4 для малой выборки и большой соответственно.
Таблица 3.3 – Определение доверительных интервалов генеральной средней для заданных вероятностей для малой (27 субъектов) выборки
| Заданная вероятность | Значение tСт | Значение предельной ошибки, кв. м/чел | Доверительный интервал, кв. м/чел |
| 0,689 | 1,058 | 1,06 | [18,34; 20,46] |
| 0,789 | 1,315 | 1,31 | [18,09; 20,71] |
| 0,889 | 1,706 | 1,70 | [17,70; 21,10] |
| 0,959 | 2,479 | 2,48 | [16,92; 21,88] |
Таблица 3.4 – Определение доверительных интервалов генеральной средней для заданных вероятностей для большой (35 субъектов) выборки
| Заданная вероятность | Значение t | Значение предельной ошибки, кв. м/чел. | Доверительный интервал, кв. м/чел. |
| 0,689 | 1,01 | 0,67 | [19,73; 21,07] |
| 0,789 | 1,25 | 0,83 | [19,57; 21,23] |
| 0,889 | 1,60 | 1,06 | [19,34; 21,46] |
| 0,959 | 2,05 | 1,36 | [19,04; 21,76] |
Как мы видим, в обеих выборках выборочная средняя величина лежит довольно близко к генеральному среднему. Однако в большей выборке выборочная средняя гораздо ближе к генеральному среднему, это связано с тем, что большая выборка более точная.
Для всех заданных вероятностей значение генеральной средней лежит в доверительном интервале. Это свидетельствует о том, что нами был выбран правильный способ отбора регионов для оценки.
Доверительные интервалы для обеих выборок имеют разную длину из-за получившейся большой выборочной дисперсии в первой (малой) выборке. В целом, мы видим, что при увеличении доверительной вероятности доверительный интервал расширяется и в том и другом случае – мы можем гарантировать, что больший доверительный интервал будет иметь внутри себя генеральную среднюю с высокой вероятностью.
Анализ динамики
Проанализируем динамику показателя «Площадь жилищ, приходящаяся в среднем на одного жителя, по Челябинской области за 2000–2009 гг.; кв. м/чел.».
Для этого построим ряд динамики и рассчитаем показатели ряда динамики:
– абсолютное изменение уровня ряда:
·
· цепное: 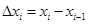
· базисное: 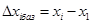
– ускорение уровня ряда:
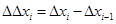
– темп роста уровня ряда:
· цепной: 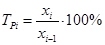
· базисный: 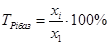
– темп прироста уровня ряда:
· цепной: 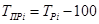
· базисный: 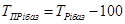
– абсолютное значение 1% прироста:
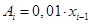
Подставим значения в формулы, полученные результаты расчетов сведем в таблицу 4.1.
По данным таблицы 4.1 построим график тенденции показателя по Челябинской области для выявления вида уравнения динамики.
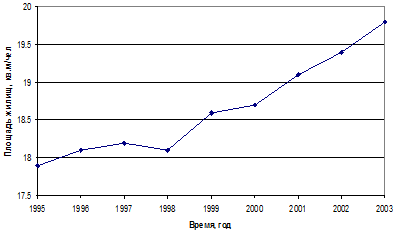
Рисунок 4.1 – График тенденции показателя по Челябинской области
Исходя из вида графика, можно судить о характере тренда. На графике ясно видно, что тренд имеет линейный вид, пусть даже с небольшими отклонениями. Составим для линейного вида тренда систему уравнений:
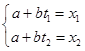 ,
,
Аппроксимируем кривую, для этого необходимо провести прямую, так чтобы площади «над ней» и «под ней» были равны. Найдем значения в соответствующих точках.
Подставив соответствующие значения t и x, получим:
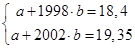
Решая систему уравнений, найдем значения a и b: 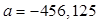 ,
, 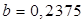 .
.
Напишем уравнение линейного тренда: 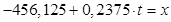
Максимальный темп прироста мы наблюдаем в 1999 году, что связано с общим ростом отечественного производства после дефолта 1998 года. Минимальный абсолютный темп прироста наблюдается в 1998 году, это связано, видимо с тем, что большая часть населения хранила свои сбережения либо в валюте, либо в банках РФ, которые после дефолта стали неплатежеспособными.
Проведя анализ динамики, мы выяснили, что площадь жилищ, приходящаяся на одного жителя, из года в год увеличивается, что говорит о постоянном увеличении уровня жизни населения. Не исключено что в дальнейшем условия жизни населения в Челябинской области улучшатся и рост площади жилищ, приходящейся на одного жителя, будет увеличиваться по другому закону, например, по параболическому.
Заключение
Проведя работу можно сделать вывод: существуют субъекты РФ в которых показатель«площадь жилищ, приходящаяся в среднем на одного жителя» выше среднего по России (20,2 кв. м/чел.), но существуют такие где показатель ниже среднего. Но необходимо сделать оговорку, что разброс данных невелик. Есть отдельные субъекты, которые были убраны из расчетов (Чеченская Республика и Республика Ингушетия), но это связано с боевыми действиями на Кавказе.
В целом по России распределение равномерное и в процентном отношении составило: 48,75% (ниже среднего) к 51,25% (выше среднего). Однако, показатель эксцесса свидетельствует о том, что разброс достаточно велик.
В результате вариационного анализа выяснили, что мода равна 19,15 кв. м/чел., а медиана 21,15 кв. м/чел. Это говорит о том что на половину жителей приходится больше чем 21,15 кв. м жилой площади, а на вторую половину жителей меньше чем 21,15 кв. м площади.
Также в работе выполнено выборочное наблюдение. Был произведен бесповторный отбор 27 и 35 регионов. То, что полученные значения выборочной средней находятся довольно близко к генеральной средней, а все доверительные интервалы содержат в себе генеральную среднюю, говорит о том, что выборки получились репрезентативными и способ отбора выбран правильно.
Челябинская область имеет значение показателя ниже среднего по России, но значение отличается менее чем на 2% (19,8 кв. м/чел.). Но прослеживается динамика увеличения показателя, это стало видно после проведения анализа динамики. Средний темп роста составил 101,3%.
Цель курсовой работы достигнута. Мы научились работать со статистическими данными. Знание основных методов статистики помогло нам успешно решить различного рода задачи.
Список литературы
группировка вариационный статистика кумулят
1. Лазарева Г.В., Богданчикова М.Ю. Статистика: Учебное пособие по выполнению курсового проекта. – Челябинск: Изд. ЮУрГУ
2. Сборник «Российский статистический ежегодник» 2010.
3. Ефимова М.Р. Общая теория статистики: Учебник для вузов. – М.: ИНФРА-М, 1998.
4. Общая теория статистики / под ред. О.Э. Башиной, А.А. Спирина. – М.: Финансы и статистика, 1999.
5. Неганова Л.М. Статистика / М.: Из. Экзамен, 2009 г.
Размещено на Allbest.ru
