Уравнение дуги окружности в комплексной форме.

При изменении параметров одного из элементов сложной цепи токи всех ветвей, на­пряжения на всех элементах изменяются так, что концы векторов этих величин описывают дуги некоторых окружностей. Для исследования за­висимости любой векторной величины (U, I) от переменного параметра доста­точно определить дугу окружности, по которой пере­мещается конец этого век­тора, другими словами, построить круговую диаграмму.

Уравнение дуги окружности в комплексной форме имеют вид:

,

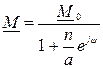где М = Мe^jb – исследуемый вектор, M₀ - вектор-хорда дуги окружности, a = const – посто­янный коэффициент, y = const – постоянный угол, n = var = (0 - ¥) – переменный параметр.

Порядок построения круговой диаграммы по заданному уравнению:

		Рис. 80

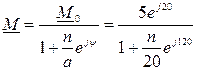
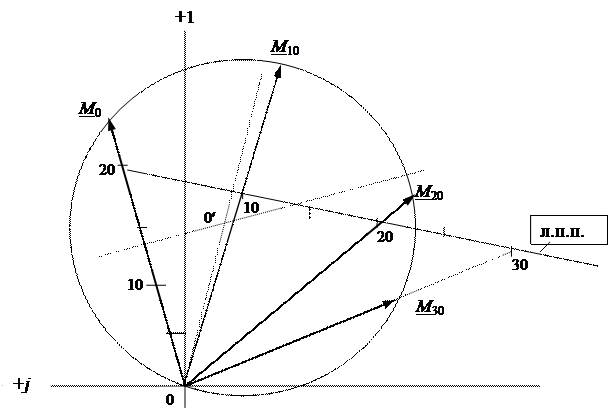
1) На комплексной плоскости в выбранном масштабе m_м откладывают вектор М₀=5e^j20 - хорду дуги окружности (рис. 80).

2) Вдоль вектора-хорды М₀ от его начала в выбранном масштабе m_а от­кладывают отрезок, равный коэффициенту “а”.

3) Из конца отрезка “а” под углом -y к вектору М₀ проводят линию пе­ременного параметра (л.п.п.), на которой наносят масштаб m_а, принятый ранее для отрезка “а”.

4) Определят положение центра дуги как точку пересечения двух пер­пендикуляров: первый проводят через середину вектора-хорды М₀, а второй – из начала координат к линии переменного параметра.

5) Проводят рабочую дугу по ту сторону от вектора-хорды М₀, где рас­положена линия переменного параметра.

6) Вдоль линии переменного параметра откладывают текущее значение параметра “n” соединяют точку с началом вектора М₀ (началом координат) и продолжают прямую линию до пересечения с дугой окружности. Искомый век­тор М соответствует отрезку от начала координат до точки пересечения прямой линии с дугой окружности, при этом модуль вектора равен длине отрезка в масштабе m_м, а начальная фаза вектора – углу между вещественной осью +1 и напрвлением вектора.

На рис. 80 показано семейство векторов М, построенных для различных значений переменного параметра “n” (n= 0; 10; 20; 30).

2. Круговая диаграмма тока и напряжений для элементов последо­вательной цепи

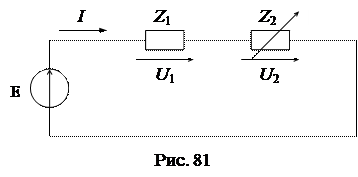
Рассмотрим схему цепи, состоящую из последовательно включенных ис­точника ЭДС E и пассивных элементов Z₁,и Z₂ (рис. 81). Задано, что E = Ee^ja=const, Z₁ = Z₁e^jj1 = const, Z₂ = Z₂e^jj2, где j₂=const, a Z₂ = var= 0÷¥ - пере­менный параметр.

Преобразуем уравнение закона Ома для схемы к виду дуги окружности в комплексной форме:

,

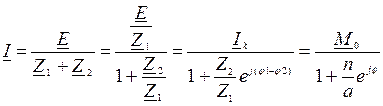где М₀ = I_к= E/Z₁ – ток короткого замыкания, соответствует вектору-хорде дуги окружно­сти, Z₂ = n = var – переменный параметр, Z₁= a = const- постоянный коэффициент, j₂ -j₁= y = const – постоянный угол.

Таким образом, уравнение для тока I является уравнением дуги окружно­сти.

Напряжение на первом элементе представляет собой уравнение дуги ок­ружности:

.

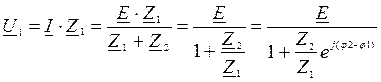Напряжение на втором элементе представляет собой уравнение дуги ок­ружности:

.

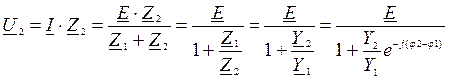Для каждого из векторов I, U₁, U₂ может быть построена круговая диа­грамма со­гласно полученным уравнениям и по ним исследована их зависимость от переменного па­раметра n = Z₂.