Переходные процессы в цепи RLC.
Переходные процессы в цепи RLC имеют особенности, связанные с учетом одновременного действия электрического и магнитного полей.
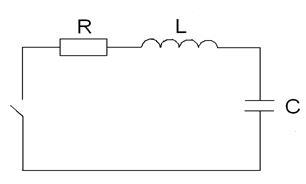
Рассмотрим цепь, состоящую из последовательно включенных электронов цепи R, L, C.
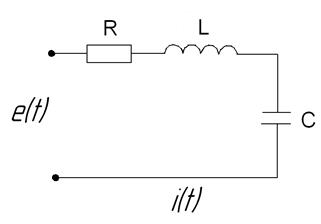
Для определения тока в цепи составим уравнение по II закону Кирхгофа
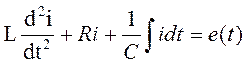
или
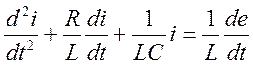
Ток определяется как решение дифференциального уравнения 2го порядка. Известно, что решение складывается из свободной и вынужденной составляющих.
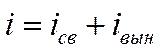
Рассмотрим свободную составляющую.
а)Свободные процессы в цепи RLC.
Свободные процессы будут иметь при e(t)=0 и коротком замыкании цепи. Будем считать, что замыкание произошло в тот момент, когда вся энергия сосредоточена в конденсаторе, (т.е. конденсатор заряжен, ток в цеп равен 0):
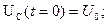
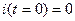 .
.
Свободную составляющую тока  получим как решение одного дифференциального уравнения.
получим как решение одного дифференциального уравнения.
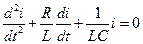
Характеристическое уравнение
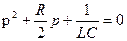
Корни характеристического уравнения:
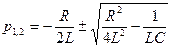
Введем обозначениея
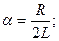
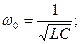
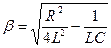 .
.
Тогда
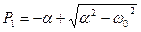 или
или 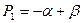
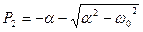 или
или 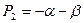
Решение дифференциального уравнения имеет вид:
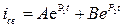
Или
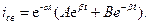 (1)
(1)
Определим постоянные коэффициенты А и В из начальных уравнений: при t=0, Uc=U0, i(0)=0
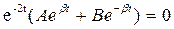
Подставив сюда t=0 получим
А=-В
Тогда
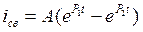 (2)
(2)
Определим А. Запишем уравнение по II закону Кирхгофа для начального момента t=0.
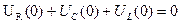

т.к. i(0)=0,то 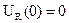 . Поэтому
. Поэтому 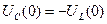 или
или
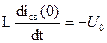
Откуда 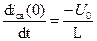
Вычислим производную: (для определения А).
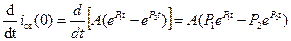
При t=0, 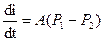 .
.
Т.о. 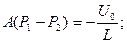
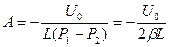
Окончательное выражение для тока имеет вид:
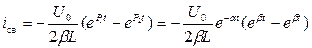 (3)
(3)
Напряжение на индуктивности
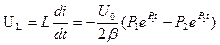 (4)
(4)
Напряжение на емкости
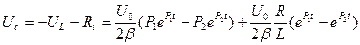
или
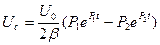 (5)
(5)
Видно, что все три величины 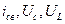 содержет составляющие е, изменяющиеся по законам
содержет составляющие е, изменяющиеся по законам 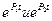 . Раскроем характер этих зависимостей. Известно, что
. Раскроем характер этих зависимостей. Известно, что 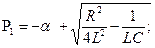
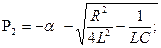
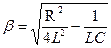 ─ может быть вещественной или мнимой величиной
─ может быть вещественной или мнимой величиной
1) если 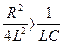 или
или 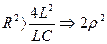 ,
, 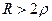 , то β ─ вещественно; корни характеристического уравнения вещественная величина.
, то β ─ вещественно; корни характеристического уравнения вещественная величина.
2) если 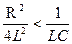 , т.е
, т.е 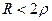 , то β ─ мнимая величина, корни характеристического уравнения оказываются комплексными.
, то β ─ мнимая величина, корни характеристического уравнения оказываются комплексными.
В зависимости от характера величины β (т.е. от соотношения между активным R и характеристическим сопротивлением 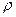 ) имеет место различный характер свободной составляющей переходного процесса.
) имеет место различный характер свободной составляющей переходного процесса.
1) при 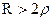 в цепи RLC протекает т.н. апериодический процесс. Этот процесс характеризуется тем, что конденсатор разряжается, но ток расхода
в цепи RLC протекает т.н. апериодический процесс. Этот процесс характеризуется тем, что конденсатор разряжается, но ток расхода
i 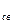 растет от 0 до i
растет от 0 до i 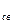 максимального и далее асимметрически уменьшается до нуля.
максимального и далее асимметрически уменьшается до нуля.
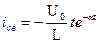

Изменение напряжения на емкости при периодическом разряде в цепи R, L, C.

Изменение тока в цепи R, L ,C при апериодическом разряде емкости.
Такое изменения тока расхода конденсатора имеет место потому, что при t=(0+) ток в цепи не может установиться сразу максимальным; 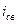 (0+)=0 .
(0+)=0 .
Мгновенному установлению максимального тока (как в RC цепи) препятствует индуктивность.
Напряжения 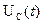 и
и 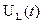 имеют следующие характеристические изменения
имеют следующие характеристические изменения
3) при R>2 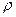 , тогда
, тогда
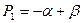
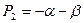
где 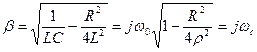
т.е. 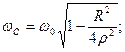
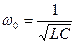
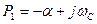
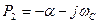
Определим закон изменения тока. Известно, что в общем случаи
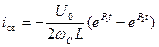 ;
;
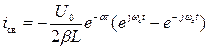
Учитывая , что 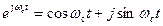 , получим
, получим
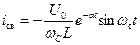 (6)
(6)
Напряжение на конденсаторе
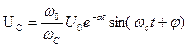 (7)
(7)
Напряжение на индуктивности
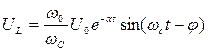 (8)
(8)
Из выражений 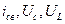 видно, что эти величины изменяются по гармоническому закону, причем амплитуда колебаний убывают по экспоненциальному закону(т.н. затухающий периодический процесс). Закон убывания определяется множителем
видно, что эти величины изменяются по гармоническому закону, причем амплитуда колебаний убывают по экспоненциальному закону(т.н. затухающий периодический процесс). Закон убывания определяется множителем 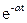
α называется коэффициентом затухания. Чем больше( 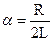 ), тем быстрее затухает колебательный процесс.
), тем быстрее затухает колебательный процесс.
Если контур без потерь, то
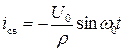 (9)
(9)
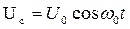 (10)
(10)
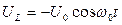 (11)
(11)
