Локальный и глобальный минимум

План лекции

1.Математическая формулировка задачи оптимизации

2. Унимодальный и мультимодальный критерий 3.Локальный и глобальный минимум

4.Выпуклое множество допустимых значений вектора варьируемых параметров

5. Выпуклый критерий оптимальности

6. Условия существования минимума в безусловных задачах оптимизации

6.1. Одномерная задача оптимизации

6.2. Многомерная задача безусловной оптимизации

7. Условия существования минимума в условных задачах оптимизации

7.1. Задача условной оптимизации с ограничениями типа равенств Функция Лагранжа

7.1.1. Теорема Лагранжа для задачи оптимизации с ограничениями типа равенств

7.2. Задача условной оптимизации с ограничениями типа неравенств

7.2.1. Понятия активных и неактивных ограничений

7.2.2. Теорема Куна-Таккера для задачи условной оптимизации с ограничениями типа неравенств

7.3. Задача условной оптимизации с ограничениями типа равенств и неравенств

7.3.1. Теорема Куна-Таккера для общей задачи условной оптимизации с ограничениями типа равенств и типа неравенств

8. Классификация задач оптимизации

9. Примеры решения задачи оптимизации

9.1. Задача оптимального проектирования емкости

9.2. Задачи на минимизацию функции, заданной в аналитической форме

Вопросы для самопроверки к лекции 2

Математическая формулировка задачи оптимизации

, (1)

при ограничениях:

(2)

(3)

где – критерий оптимальности (скаляр);

– вектор варьируемых параметров;

Отметим, что

Задача поиска минимума или максимума критерия оптимальности(целевой функции) называется задачей оптимизации, другими словами задачей поиска экстремума.

Задача (1), (2), (3) – это задача условной оптимизации.

Если ограничения (2), (3) отсутствуют, то это задача безусловной оптимизации.

Унимодальный и мультимодальный критерий

Одномерный случай унимодальной функции (n=1).

Критерий оптимальности , где , называется унимодальным критерием оптимальности, если существует точка такая, что на полуинтервале функция убывает, а на полуинтервале – возрастает.

Двумерный случай унимодальной функции (n=2)

Критерий оптимальности 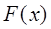, имеющий в области определения несколько локальных минимумов, называется мультимодальным критерием оптимальности или многоэкстремальным критерием оптимальности.

Одномерный случай мультимодальной функции (n=1)

Локальный и глобальный минимум

Локальный минимум в точке

– некоторая малая окрестность точки

Глобальный минимум в точке

Где – область допустимых значений .

Точка наименьшего из всех локальных минимумов называется точкой глобального минимума функции . Соответствующее значение функции называется глобальным минимумом этой функции

На рисунке для одномерного случая: - точки локального минимума функции , – соответствующие локальные минимумы этой функции, – точка глобального минимума, а – глобальный минимум этой функции.