Доказательство. Из условия (1) вытекает, что
Из условия (1) вытекает, что 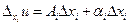 . Тогда
. Тогда 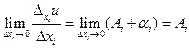 , так как
, так как 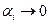 при
при 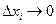 . Теорема доказана.
. Теорема доказана.
Следствие 1. Условие (2) можно записать в следующей форме: 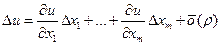 .
.
Следствие 2. Если функция f дифференцируема в точке  , то представление (1) или (2) единственно, то есть числа Ai, равные частным производным, определяются единственным образом.
, то представление (1) или (2) единственно, то есть числа Ai, равные частным производным, определяются единственным образом.
Теорема 2. Если функция дифференцируема в точке  , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Доказательство.В самом деле, из условия (1) дифференцируемости вытекает, что 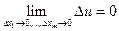 , а это означает, что функция непрерывна в точке
, а это означает, что функция непрерывна в точке  .
.
3. Геометрический смысл условия дифференцируемости функции двух переменных. Достаточные условия дифференцируемости
Мы уже обратили внимание, что из существования функции всех частных производных в точке не вытекает её непрерывность в этой точке, и тем более, дифференцируемость. Докажем следующую теорему.
Теорема 3. Если функция f имеет все частные производные в некоторой окрестности точки 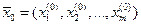 и все эти частные производные непрерывны в точке
и все эти частные производные непрерывны в точке 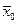 , то функция f дифференцируема в точке
, то функция f дифференцируема в точке 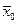 .
.
Доказательство. Для сокращения записи проведем доказательство для функции двух переменных u=f(x,y). Итак, пусть обе частные производные 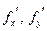 существуют в окрестности точки (x0,y0) и непрерывны в этой точке. Взяв приращения
существуют в окрестности точки (x0,y0) и непрерывны в этой точке. Взяв приращения 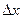 и
и 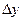 столь малыми, чтобы не выйти из указанной окрестности, рассмотрим приращение
столь малыми, чтобы не выйти из указанной окрестности, рассмотрим приращение 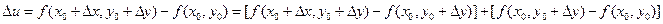 Выражение
Выражение 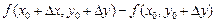 можно рассматривать как приращение функции
можно рассматривать как приращение функции 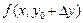 одной переменной x на отрезке
одной переменной x на отрезке 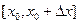 . Тогда согласно теореме Лагранжа найдется такое
. Тогда согласно теореме Лагранжа найдется такое 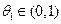 ,
,
что 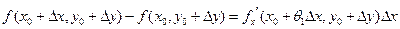 . Аналогично,
. Аналогично, 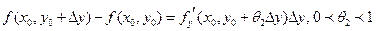 .
.
Так как 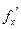 и
и 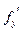 непрерывны в точке (x0,y0), то
непрерывны в точке (x0,y0), то 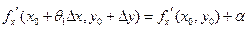 ,
, 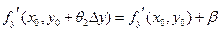 , где α и β – бесконечно малые при
, где α и β – бесконечно малые при 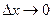 и
и 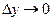 функции. Используя это, получим:
функции. Используя это, получим: 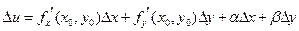 . Это равенство означает дифференцируемость функции f в точке (x0,y0). Теорема доказана.
. Это равенство означает дифференцируемость функции f в точке (x0,y0). Теорема доказана.
4. Дифференцирование сложной функции
Рассмотрим сложную функцию 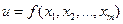 , где
, где 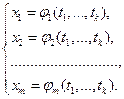 (3)
(3)
Теорема 4. Пусть функции (3) дифференцируемы в точке 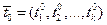 , а функция u=f(x1,x2,…,xm) дифференцируема в точке
, а функция u=f(x1,x2,…,xm) дифференцируема в точке 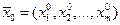 , где
, где 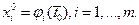 Тогда сложная функция
Тогда сложная функция 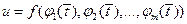 дифференцируема в точке
дифференцируема в точке 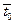 , при этом частные производные вычисляются по формулам
, при этом частные производные вычисляются по формулам 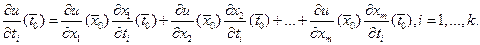
Доказательство. Возьмем приращения 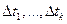 . Им соответствуют приращения
. Им соответствуют приращения 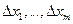 функций (3) в точке
функций (3) в точке 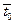 . Приращениям,
. Приращениям, 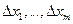 в свою очередь, соответствует приращение
в свою очередь, соответствует приращение 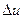 функций u=f(x1,x2,…,xm) в точке
функций u=f(x1,x2,…,xm) в точке 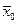 . Так как функция f дифференцируема в точке
. Так как функция f дифференцируема в точке 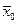 , то
, то 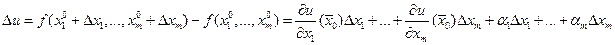 . В силу дифференцируемости функций (3) в точке
. В силу дифференцируемости функций (3) в точке 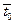
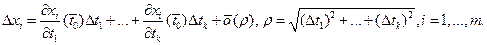
Подставив последние равенства, получим: 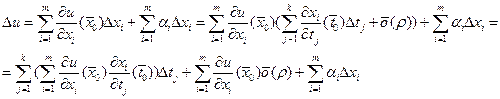
Осталось доказать, что последние две суммы представляют собой величину 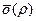 . Очевидно, что
. Очевидно, что 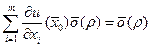 . Далее,
. Далее, 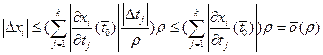 . Так как
. Так как 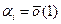 , то
, то 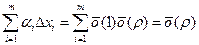 .
.
Итак, 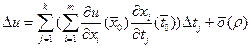 , что означает дифференцируемость сложной функции, причем
, что означает дифференцируемость сложной функции, причем 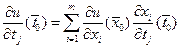 . Теорема доказана.
. Теорема доказана.
Замечание. Рассмотрим важный частный случай, когда 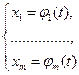 . Тогда
. Тогда 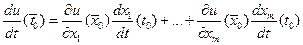 .
.
5. Дифференциал функции многих переменных. Инвариантность формы первого дифференциала.
Определение. Дифференциалом 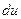 дифференцируемой в точке
дифференцируемой в точке  функции u=f(x1,x2,…,xm) называется главная линейная относительно приращений аргументов часть приращения этой функции в точке
функции u=f(x1,x2,…,xm) называется главная линейная относительно приращений аргументов часть приращения этой функции в точке  , то есть
, то есть 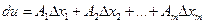 .
.
Используя теорему 1, перепишем 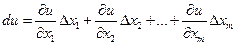 .
.
Введем понятие дифференциала 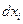 независимой переменной
независимой переменной 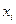 . Под дифференциалом
. Под дифференциалом 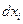 независимой переменной
независимой переменной 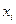 можно понимать любое число. Будем брать это число, равным приращению
можно понимать любое число. Будем брать это число, равным приращению 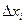 независимой переменной
независимой переменной 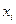 . Тогда
. Тогда 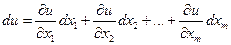 (4)
(4)
Докажем, что формула (4) справедлива и в том случае, когда аргументы x1,x2,…,xm сами являются дифференцируемыми функциями некоторых новых переменных t1,t2,…,tk. Это свойство называют свойством инвариантности формы первого дифференциала.
Пользуясь теоремой 4, получим 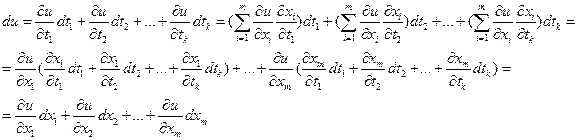
Свойство инвариантности формы первого дифференциала позволяет установить следующие правила дифференцирования. Пусть u и v – дифференцируемые функции. Тогда 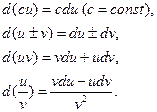
Докажем, например, справедливость третьего равенства. Рассмотрим функцию 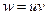 двух переменных u и v. Тогда
двух переменных u и v. Тогда 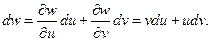 В силу инвариантности формы первого дифференциала выражение
В силу инвариантности формы первого дифференциала выражение 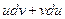 будет дифференциалом функции
будет дифференциалом функции 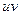 и в случае, когда u и v сами являются дифференцируемыми функциями каких-либо переменных.
и в случае, когда u и v сами являются дифференцируемыми функциями каких-либо переменных.
Задание. Доказать остальные равенства.
6. Производная по направлению. Градиент.
Начнем с рассмотрения функции трех независимых переменных 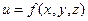 . Пусть эта функция определена в некоторой окрестности точки M0(x0,y0,z0) и дифференцируема в этой точке.
. Пусть эта функция определена в некоторой окрестности точки M0(x0,y0,z0) и дифференцируема в этой точке.
Рассмотрим всевозможные лучи, выходящие из точки M0(x0,y0,z0). Каждый такой луч задается единичным вектором 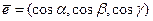 .
.
Взяв на прямой, содержащей этот луч, точку M(x,y,z), рассмотрим вектор 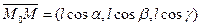 , где l – длина отрезка M0M. С другой стороны,
, где l – длина отрезка M0M. С другой стороны, 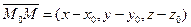 . Сопоставляя эти равенства, получим:
. Сопоставляя эти равенства, получим: 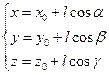
и рассмотрим сложную функцию одной переменной l 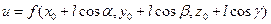 .
.
Определение. Производную указанной сложной функции по переменной l, взятой в точке l=0, называют производной функции u=f(x,y,z) в точке M0(x0,y0,z0) по направлению вектора 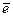 , и обозначают символом
, и обозначают символом 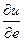 .
.
Согласно теореме 4, 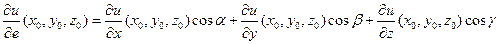 . (5)
. (5)
Определение.Градиентом функции u=f(x,y,z) в точке M0(x0,y0,z0) называют вектор с координатами 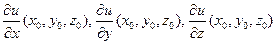 . Вектор градиент обозначают символом grad u.
. Вектор градиент обозначают символом grad u.
Итак, 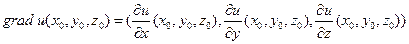 . Тогда производная по направлению является скалярным произведением вектора
. Тогда производная по направлению является скалярным произведением вектора 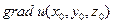 и вектора
и вектора 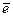 :
: 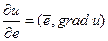 . Так как
. Так как 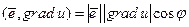 , где φ – угол между векторами
, где φ – угол между векторами 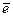 и
и 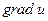 , а
, а 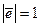 , то
, то 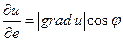 . Тогда максимальное значение
. Тогда максимальное значение 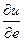 получается при
получается при 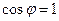 , то есть при совпадении направления
, то есть при совпадении направления 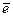 с направлением
с направлением 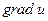 , причем в этом направлении
, причем в этом направлении 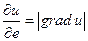 .
.
Итак, мы доказали два утверждения:
1. производная функции u=f(x,y,z) в точке (x0,y0,z0) по направлению, определенному градиентом этой функции в указанной точке, имеет максимальное значение по сравнению с производной в этой точке по любому другому направлению;
2. значение производной по направлению, определенному градиентом этой функции в данной точке, равно 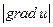 , то есть длине вектора
, то есть длине вектора 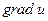 в данной точке.
в данной точке.
Для выполнения геометрического смысла вектора 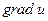 введем понятие поверхностей уровня функции u=f(x,y,z). Множество точек, удовлетворяющих уравнению f(x,y,z)=c=const, называется поверхностью уровня.
введем понятие поверхностей уровня функции u=f(x,y,z). Множество точек, удовлетворяющих уравнению f(x,y,z)=c=const, называется поверхностью уровня.
В каждой точке (x0,y0,z0) поверхности уровня f(x,y,z)=c нормальным вектором к касательной плоскости будет являться вектор 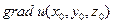 , другими словами, вектор
, другими словами, вектор 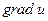 ортогонален к поверхности уровня.
ортогонален к поверхности уровня.
Аналогичные выводы можно сделать относительно производной по направлению и вектора 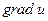 для функции m переменных, в частности для функции двух переменных.
для функции m переменных, в частности для функции двух переменных.
Задание. Провести выкладки самостоятельно.
Частные производные и дифференциалы высших порядков
7. Частные производные высших порядков
Пусть частная производная 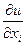 функции u=f(x1,x2,…,xm), определенной на области G, существует в каждой точке этой области. Таким образом,
функции u=f(x1,x2,…,xm), определенной на области G, существует в каждой точке этой области. Таким образом, 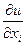 представляет собой функцию переменных x1,…,xm, также определенную на области G. Если эта функция
представляет собой функцию переменных x1,…,xm, также определенную на области G. Если эта функция 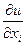 имеет частную производную по переменной xk в некоторой точке М области, то указанную частную производную
имеет частную производную по переменной xk в некоторой точке М области, то указанную частную производную 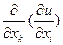 называют частной производной второго порядка функции f в точке М сначала по переменной xi, а затем по переменной xk и обозначают одним из следующих символов:
называют частной производной второго порядка функции f в точке М сначала по переменной xi, а затем по переменной xk и обозначают одним из следующих символов: 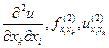 . При этом если
. При этом если 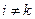 , то частная производная
, то частная производная 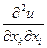 .
.
Предположим, что уже введено понятие (n-1)-ой частной производной 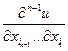 . Тогда если эта (n-1)-я частная производная имеет в точке М частную производную по переменной
. Тогда если эта (n-1)-я частная производная имеет в точке М частную производную по переменной 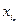 , то указанную частную производную называют n-й частной производной функции f в точке М, т.е.
, то указанную частную производную называют n-й частной производной функции f в точке М, т.е. 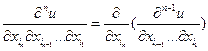 .
.
Если не все индексы 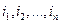 совпадают между собой, то эта частная производная называется смешанной.
совпадают между собой, то эта частная производная называется смешанной.
Таким образом, мы ввели понятие n-й частной производной индуктивно.
Далее мы выясним достаточные условия независимости смешанных производных от порядка дифференцирования.
Сначала введем важное понятие.
Определение. Пусть n=2,3,… Назовем функцию n-дифференцируемой в точке 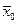 , если эта функция (n-1)-дифференцируема всюду в некоторой окрестности точки
, если эта функция (n-1)-дифференцируема всюду в некоторой окрестности точки 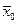 и все её частные производные порядка (n-1) являются дифференцируемыми в точке
и все её частные производные порядка (n-1) являются дифференцируемыми в точке 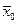 функциями.
функциями.
Заметим, что при этом для любого k, удовлетворяющего условию 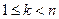 , любая её частная производная порядка k будет (n-k) дифференцируемой в этой точке. Принято также считать функцию 0-дифференцируемой в точке, если она непрерывна в этой точке.
, любая её частная производная порядка k будет (n-k) дифференцируемой в этой точке. Принято также считать функцию 0-дифференцируемой в точке, если она непрерывна в этой точке.
Для того, чтобы функция f была n-дифференцируема в точке 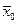 достаточно, чтобы все её частные производные n-ого порядка существовали в окрестности точки
достаточно, чтобы все её частные производные n-ого порядка существовали в окрестности точки 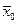 и являлись непрерывными в этой точке функциями.
и являлись непрерывными в этой точке функциями.
Справедливость этого утверждения вытекает из определения n-дифференцируемости и теоремы 3 о достаточных условиях дифференцируемости.
Теорема 1. Пусть функция u=f(x,y) 2-дифференцируема в точке M0(x0,y0). Тогда в этой точке частные производные 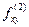 и
и 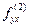 равны.
равны.
Доказательство. Так как функция f 2-дифференцируема в точке M0(x0,y0), то частные производные 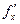 и
и 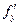 определены в некоторой
определены в некоторой 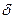 -окрестности точки M0 и дифференцируемы в этой точке.
-окрестности точки M0 и дифференцируемы в этой точке.
Рассмотрим выражение 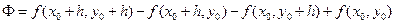 , где h достаточно мало, так что точка M0(x0+h,y0+h) находится в указанной
, где h достаточно мало, так что точка M0(x0+h,y0+h) находится в указанной 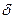 -окрестности точки M0. Выражение Ф можно рассматривать как приращение
-окрестности точки M0. Выражение Ф можно рассматривать как приращение 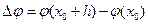 дифференцируемой на отрезке
дифференцируемой на отрезке 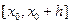 функции
функции 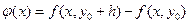 одной переменной x. Поэтому по формуле Лагранжа найдется
одной переменной x. Поэтому по формуле Лагранжа найдется 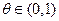 такое, что,
такое, что, 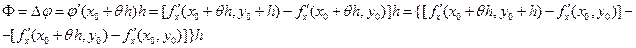 Так как
Так как 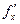 дифференцируема в точке M0, то
дифференцируема в точке M0, то 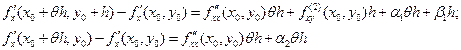 , где
, где 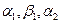 - бесконечно малые при
- бесконечно малые при 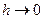 функции. Тогда
функции. Тогда 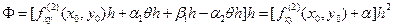 , где
, где 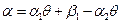 - бесконечно малая при
- бесконечно малая при 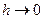 функция.
функция.
С другой стороны, рассматривая 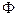 как приращение
как приращение 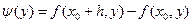 , аналогично предыдущему получим выражение для Ф:
, аналогично предыдущему получим выражение для Ф: 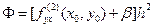 , где
, где 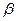 - бесконечно малая при
- бесконечно малая при 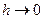 функция. Тогда
функция. Тогда 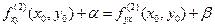 . Перейдя к пределу при
. Перейдя к пределу при 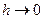 , получим
, получим 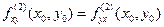 . Теорема доказана.
. Теорема доказана.
Докажем еще одну теорему о равенстве смешанных производных.
Теорема 2. Пусть в некоторой окрестности точки M0(x0,y0) функция f имеет частные производные 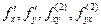 и производные
и производные 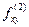 и
и 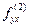 непрерывны в точке M0. Тогда
непрерывны в точке M0. Тогда 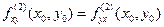 .
.
Доказательство. Воспользуемся выражением Ф из доказательства предыдущей теоремы 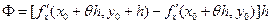 . Применяя к этой разности формулу Лагранжа по переменной y на отрезке [y0,y0+h], получим:
. Применяя к этой разности формулу Лагранжа по переменной y на отрезке [y0,y0+h], получим: 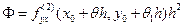 , где
, где 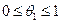 . В силу непрерывности
. В силу непрерывности 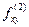 в точке M0(x0,y0) получим
в точке M0(x0,y0) получим 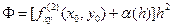 , где
, где 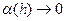 при
при 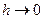 . Следовательно,
. Следовательно, 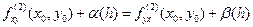 , и перейдя к пределу при
, и перейдя к пределу при 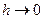 , получим
, получим 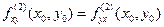 . Теорема доказана.
. Теорема доказана.
Докажем теперь теорему о независимости значения любой смешанной производной от порядка дифференцирования.
Теорема 3. Пусть функция u=f(x1,x2,…,xm) n-дифференцируема в точке 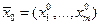 . Тогда в этой точке значение любой смешанной производной n-ого порядка не зависит от порядка дифференцирования.
. Тогда в этой точке значение любой смешанной производной n-ого порядка не зависит от порядка дифференцирования.
Доказательство.Очевидно.
Достаточно доказать равенство 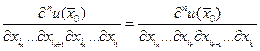 .
.
Рассмотрим функцию 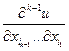 как функцию двух переменных
как функцию двух переменных 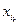 и
и 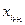 . Тогда в силу теоремы 1
. Тогда в силу теоремы 1 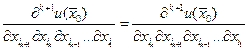 . Остальное очевидно. Теорема доказана.
. Остальное очевидно. Теорема доказана.
Отметим, что любую частную производную n-го порядка можно записать в виде 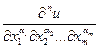 , где
, где 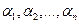 - целые числа, удовлетворяющие условиям:
- целые числа, удовлетворяющие условиям: 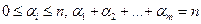 .
.
8. Дифференциалы высших порядков
Чтобы дать определение дифференциалов высших порядков, введем еще одно обозначение первого дифференциала функции u=f(x1,x2,…,xm) 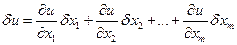 . То есть мы заменили
. То есть мы заменили 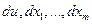 на
на 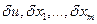 соответственно. В прежних обозначениях
соответственно. В прежних обозначениях 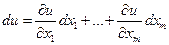 .
.
Правая часть равенства есть функция переменных x1,x2,…,xm; и если функция f 2-дифференцируема в точке M(x1,…,xm), то можно рассмотреть её дифференциал 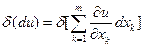 .
.
Определение. Значение 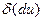 дифференциала от первого дифференциала, взятое при
дифференциала от первого дифференциала, взятое при 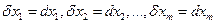 , называется вторым дифференциалом функции f (в данной точке М) и обозначается символом
, называется вторым дифференциалом функции f (в данной точке М) и обозначается символом 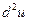 .
.
Итак, 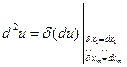 .
.
Дифференциал dnu любого порядка n введем по индукции.
Предположим, что определен дифференциал dn-1u порядка n-1 и функция f n-дифференцируема в точке M(x1,…,xm), а её аргументы x1,…,xm являются либо независимыми переменными, либо n-дифференцируемыми функциями некоторых независимых переменных t1,…,tk.
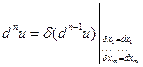 .
.
При вычислении второго и последующих дифференциалов приходится различать два случая.
1) Пусть аргументы x1,…,xm являются независимыми переменными. Тогда 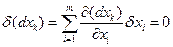 , так как
, так как 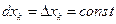 для всех точек M(x1,…,xm).
для всех точек M(x1,…,xm).
Следовательно,
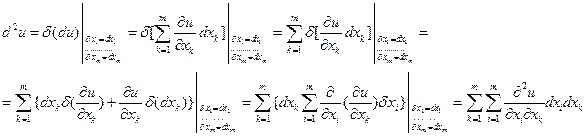
(Мы воспользовались еще и тем, что смешанные производные 2-го порядка не зависят от порядка дифференцирования).
И далее по индукции 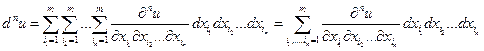 .
.
Введем формальный символ 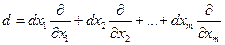 . Тогда можно записать
. Тогда можно записать 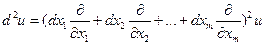 и
и 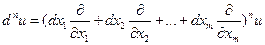 (*)
(*)
2) Пусть аргументы x1,…,xm являются 2-дифференцируемыми функциями некоторых независимых переменных t1,…,tk. Тогда 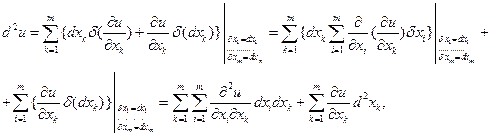
Или 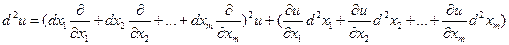 (**)
(**)
Сравнивая формулы (*) и (**), делаем вывод, что второй дифференциал уже не обладает свойством инвариантности формы. Тем более не обладают этим свойством все последующие дифференциалы.
Замечание. Укажем важный частный случай, когда 2-дифференциал и последующие дифференциалы функции u=f(x1,x2,…,xm) определяются той же самой формулой (*), что и для случая независимых переменных x1,x2,…,xm.
Пусть переменные x1,x2,…,xm являются линейными функциями независимых
переменных t1,…,tk: 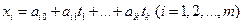 , где
, где 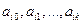 - постоянные.
- постоянные.
Так как любая частная производная выше первого порядка от линейной функции 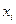 равна нулю, то
равна нулю, то 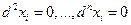 . Следовательно, n-дифференциал определяется формулой (*).
. Следовательно, n-дифференциал определяется формулой (*).
9. Формула Тейлора с остаточным членом в форме Лагранжа
Пусть функция u=f(x,y) двух переменных n-дифференцируема в окрестности точки (x,y), и 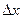 и
и 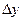 достаточно малы, чтобы точка
достаточно малы, чтобы точка 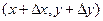 принадлежала указанной окрестности.
принадлежала указанной окрестности.
Тогда и отрезок с концами (x,y) и 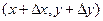 содержится в ней.
содержится в ней.
Рассмотрим сложную функцию 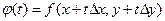 , определенную на отрезке [0,1] и дифференцируемую на нем (в силу теоремы 4 о дифференцируемости сложной функции).
, определенную на отрезке [0,1] и дифференцируемую на нем (в силу теоремы 4 о дифференцируемости сложной функции).
Имеем: 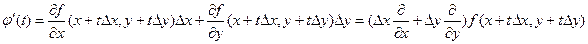 . Далее по индукции получим, что
. Далее по индукции получим, что 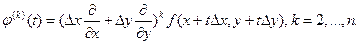
В аналогичной ситуации для функции u=f(x1,x2,…,xm) имеем: 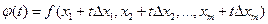 и
и 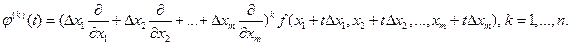
Докажем важную теорему.
Теорема 4. Пусть 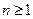 и функция u=f(x1,x2,…,xm) n-дифференцируема в некоторой окрестности точки
и функция u=f(x1,x2,…,xm) n-дифференцируема в некоторой окрестности точки  , а отрезок
, а отрезок 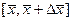 содержится в ней. Тогда
содержится в ней. Тогда 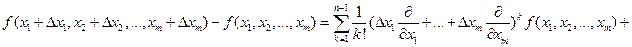
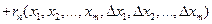 (2)
(2)
где 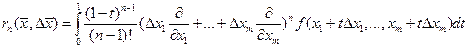 (3)
(3)
Равенство (2) называют формулой Тейлора с достаточным членом (3) в интегральной форме.
Доказательство. Рассмотрим функцию 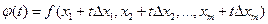 . Тогда при
. Тогда при 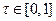 в силу формулы Тейлора для функции одной переменной
в силу формулы Тейлора для функции одной переменной 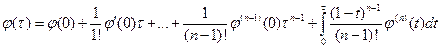 .
.
Полагая 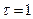 , получим:
, получим: 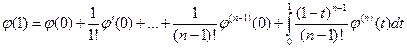 .
.
Подставляя в полученное равенство в соответствии с формулой (1) значения 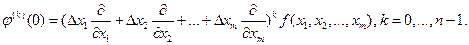
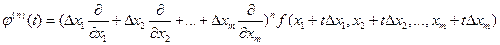 , получаем утверждение теоремы.
, получаем утверждение теоремы.
Замечание 1. Если остаточный член формулы Тейлора для функции 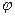 записать в форме Лагранжа, т.е.
записать в форме Лагранжа, т.е. 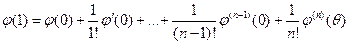 , где
, где 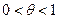 , то мы получим остаточный член формулы (2) в виде
, то мы получим остаточный член формулы (2) в виде 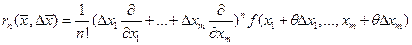 (4)
(4)
Эту форму, так же как и в случае функции одной переменной, называют формой Лагранжа остаточного члена формулы Тейлора.
Замечание 2. Формулу Тейлора с остаточным членом в форме Лагранжа можно переписать в виде: 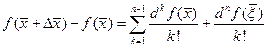 , где в дифференциале функции f
, где в дифференциале функции f 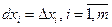 и
и 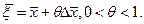
10. Формула Тейлора с остаточным членом в форме Пеано
Теорема 5. Пусть функция u=f(x1,x2,…,xm) n-дифференцируема в точке 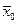 . Тогда существует непрерывная в точке
. Тогда существует непрерывная в точке 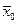 функция
функция 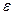 такая, что
такая, что 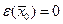 и для всех
и для всех 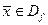 имеет место равенство
имеет место равенство 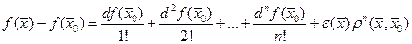 (5), где
(5), где 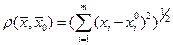 . Дифференцируемость n раз функции f в точке x0 предполагает её (n-1)-дифференцируемость в некоторой окрестности точки x0.
. Дифференцируемость n раз функции f в точке x0 предполагает её (n-1)-дифференцируемость в некоторой окрестности точки x0.
Доказательство.Положим для всех 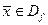
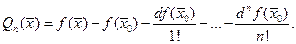 Нужно лишь доказать, что
Нужно лишь доказать, что 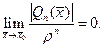
Докажем по индукции.
Для n=0 и n=1 это следует из определения соответственно непрерывности и 1-дифференцируемости функции f в точке 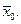
Пусть 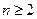 , и пусть теорема верна для i=n-1. Докажем её для i=n.
, и пусть теорема верна для i=n-1. Докажем её для i=n.
Найдем производную 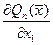 . Предварительно убедимся, что для k=1,…,n при фиксированных x2,x3,…,xm
. Предварительно убедимся, что для k=1,…,n при фиксированных x2,x3,…,xm 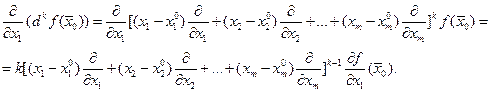
При фиксированных x2,x3,…,xm величину 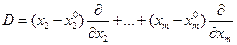 можно рассматривать как постоянную, поскольку символы
можно рассматривать как постоянную, поскольку символы 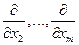 используются для образования частных производных функции f в фиксированной точке
используются для образования частных производных функции f в фиксированной точке 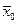 . Поэтому
. Поэтому 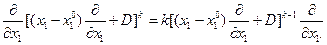 Следовательно,
Следовательно, 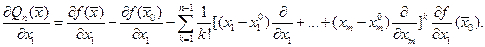 Но это есть остаточный член в формуле Тейлора порядка n-1, примененной к функции
Но это есть остаточный член в формуле Тейлора порядка n-1, примененной к функции 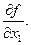 По предположению индукции
По предположению индукции 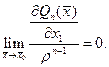 Совершенно аналогично получим, что для i=2,…,m
Совершенно аналогично получим, что для i=2,…,m 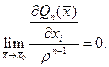 Тогда взяв точку
Тогда взяв точку  из указанной окрестности точки
из указанной окрестности точки 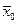 и заметив, что
и заметив, что 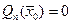 и применив формулу Тейлора порядка 1 с остаточным членом в форме Лагранжа будем иметь
и применив формулу Тейлора порядка 1 с остаточным членом в форме Лагранжа будем иметь 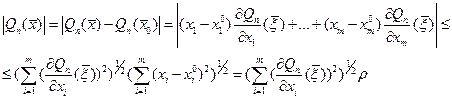
Где 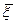 - точка, промежуточная между
- точка, промежуточная между  и
и 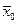 . Следовательно,
. Следовательно, 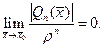 Теорема доказана.
Теорема доказана.
Замечание. Остаточный член формулы (5) в виде 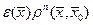 записывают короче в виде
записывают короче в виде 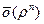 , где
, где 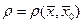 , и называют остаточным членом в форме Пеано.
, и называют остаточным членом в форме Пеано.
