Скорость и ускорение как производная координаты

Движение

Движением тела называется изменение его положения в пространстве относительно других.

Координата— величина, служащая для определения положения какой-либо точки на плоскости или в пространстве.

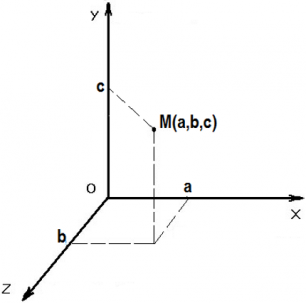
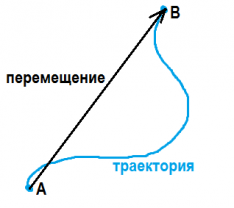
Перемещением тела называется вектор, соединяющий начальное положение тела с его последующим положением.

Траектория— это линия, вдоль которой движется тело.

Путь — это длина траектории, вдоль которой движется тело.

Прямолинейным равномерным движением называется движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.

Скоростью равномерного прямолинейного движения называется величина, равная отношению перемещения тела 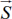к времени t, за которое это перемещение произошло .

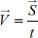Скорость ― это векторная величина!

В заданиях, где дана зависимость скорости тела от времени.

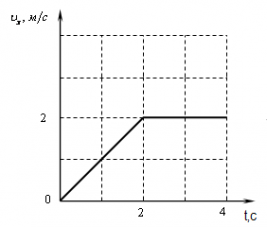
Пройденный путь можно вычислить как площадь под графиком.

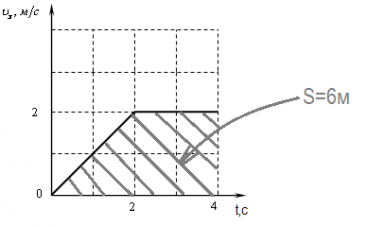
Ускорением тела называется векторная величина, равная отношению изменения скорости за любой промежуток времени к величине этого промежутка .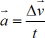

Зависимость скорости от времени при наличии ускорения даётся выражением 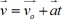, где:

― скорость тела в момент времени t;

t ― время;

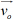― начальная скорость тела;

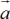― ускорение тела.

Равноускоренным движением тела называется движение, при котором его ускорение не меняется, ни по величине, ни по направлению.

Уравнение равноускоренного движения в проекции на ось х имеет вид:

x(t) = x0 + v0t + .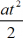

Где x0 ― начальная координата тела;

v0 ― проекция начальная скорость на ось x;

a ― проекция ускорения на ось x;

t ― время движения.

Скорость и ускорение как производная координаты

Если существует зависимость координаты от времени x(t), то зависимость скорости от времени можно получив взяв производную по времени от этой зависимости. Скорость― это производная координаты тела по времени vx(t) = x'(t). Например, если зависимость координаты тела при равноускоренном движении имеет вид x(t) = 6 – 2t + 12t2, то, взяв первую производную от координаты мы получим зависимость скорости тела от времениvx(t) = –2 + 12 ∙ 2t = –2 + 24t.

Точно также, ускорение― это производная от скорости тела. ax(t) = vx'(t).

Движение по окружности

При движении по окружности часто удобно использовать не обычную скорость, аугловую скорость.

Угловая скорость численно равна углу поворота радиуса за единицу времени.

Угловая скорость для тела, двигающегося из точки 1 в точку 2, будет равна:

ω = 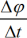, где

∆φ ― угол поворота [рад],

∆t ― промежуток времени [с],

ω ― угловая скорость .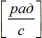

Линейную скорость точки на определенном расстоянии (радиусе) R от оси вращения можно считать как: v = ωR.

Соответственно, чем больше будет радиус окружности, тем больше будет линейная скорость, при постоянной угловой скорости.

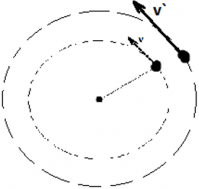
Период— время, за которое тело делает полный оборот по окружности.

T = 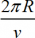, где

T ― период [с],

R ― радиус окружности [м],

v ― скорость .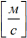

Частота— равна количеству оборотов по окружности, совершенных за единицу времени.

v = 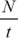, где

v ― частота [Гц],

t ― время [c],

N ― количество оборотов.

При движении по окружности тело, в каждый момент времени, меняет направление своей скорости, а, значит, двигается с ускорением.

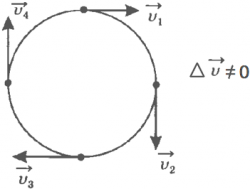
Ускорение, которое испытывает тело, движущееся по окружности, называется нормальным или центростремительным и всегда направленно к центру окружности.

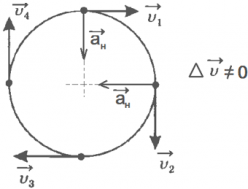
Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой :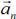

an = 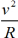, где

R ― радиус окружности [м],

an ― нормальное ускорение ,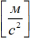

v ― скорость 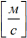.