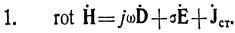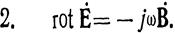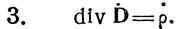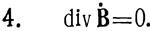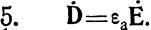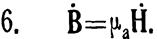Уравнения Максвелла для монохроматических колебаний. Комплексные амплитуды полей

Все реальные электромагнитные процессы можно представить либо в виде суммы дискретных гармонических колебаний, либо в виде непрерывного спектра гармонических колебаний. Поэтому изучение гармонических во времени электромагнитных полей представляет большой практический и теоретический интерес. Такие поля часто называют также монохроматическими.

Анализ гармонических процессов существенно упрощается при использовании метода комплексных амплитуд. В этом случае вместо любой скалярной функции, изменяющейся по закону

где ψm- амплитуда; φ - начальная фаза; ω = 2πf = 2π/T; a f и T-частота и период гармонического колебания, вводится в рассмотрение комплексная функция

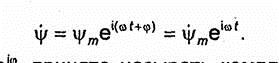
В систему уравнений Максвелла входят частные производные по x,y,z,t. Для упрощения исключим одну из переменных, это возможно при монохроматическом процессе, когда изменение полей во времени происходит по гармоническому закону с частотой w.

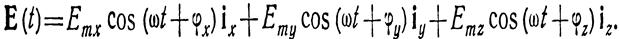
Ex,Ey,Ez - амплитуды отдельных составляющих поля.
ɸ_x,ɸ_y,ɸ_z - фазовые углы(начальные фазы).
E(t) описывает эллипс и в комплексной форме:

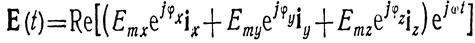
Вектор

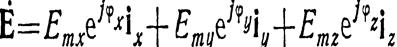
Введем комплексные амплитуды в уравнение Максвелла