Простейшие свойства линейного оператора

1º. Линейный оператор 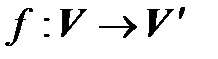переводит нейтральный элемент пространства 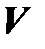в нейтральный элемент пространства .

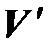►Пусть 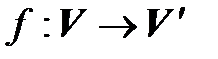– линейный оператор. Тогда .◄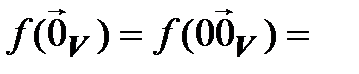

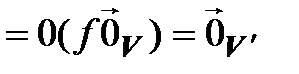2º. При линейном операторе линейно зависимые векторы пространства 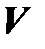переходят в линейно зависимые векторы пространства .

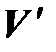►Пусть 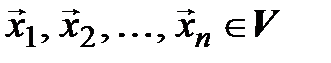– линейно зависимые векторы. Это значит, что существуют числа 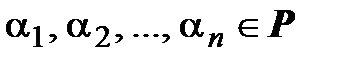, не все равные нулю, такие, что

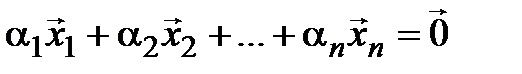. (4.7)

Подействуем линейным оператором 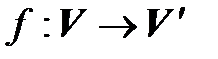на обе части равенства (4.7). Тогда

(4.7) 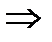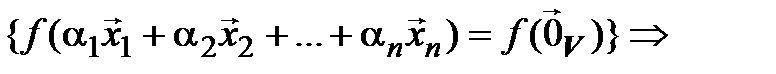[(4.3) и 1º]

.

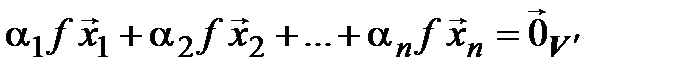Так как среди чисел 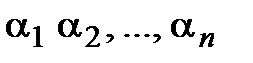есть отличные от нуля, то система { 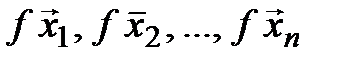} линейно зависима.◄

Вопрос 17

Определение матрицы линейного оператора. Связь координат вектора с координатами его образа

Пусть в линейном пространстве 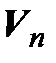над полем 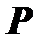задан базис

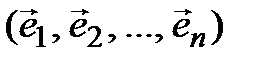(4.8)

и пусть 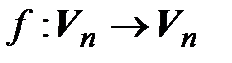– линейный оператор (читается так: 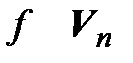в себя). Построим систему векторов

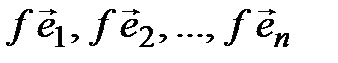( ). (4.9)

Каждый из векторов системы (4.9) можно разложить по базису (4.8):

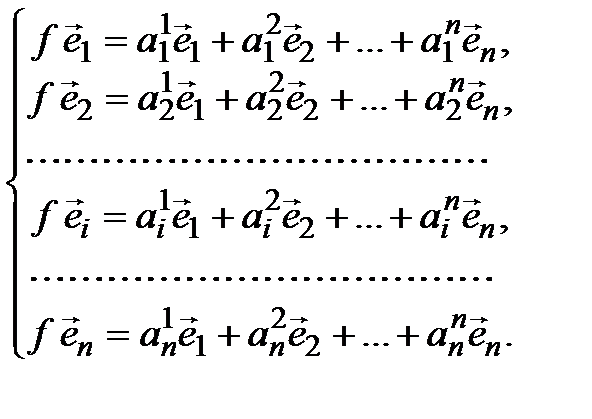(4.10)

Сокращенно система (4.10) записывается одним равенством:

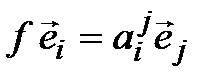. (4.11)

Расположим числа 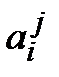в матрицу А по нашей договоренности: верхний индекс обозначает номер строки, а нижний – номер столбца:

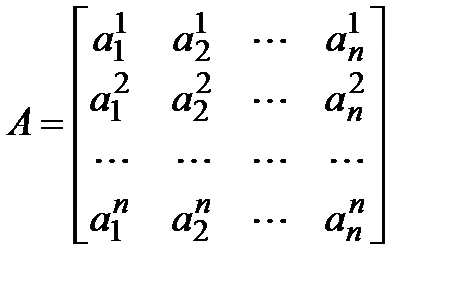
Заметим, что столбцы полученной матрицы А являются координатными столбцами образов векторов базиса (4.8) в том же базисе. Обозначим

[ ] = .

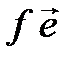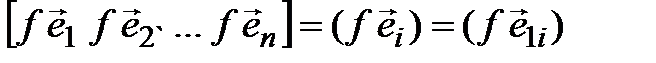Равенство (4.11) можно переписать и так: 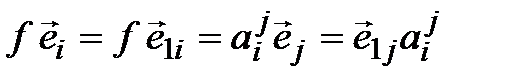, откуда, руководствуясь правилом цепочки, (4.11) записываем в матричном виде:

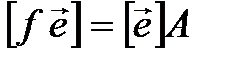. (4.12)

Матрицей линейного оператора 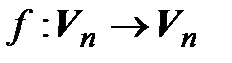в некотором базисе называется матрица А, столбцами которой являются координатные столбцы образов базисных векторов в том же базисе. Это матрица 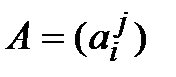, элементы которой удовлетворяют системе равенств (4.10) или (4.11), а сама матрица удовлетворяет матричному равенству (4.12).

Примеры

1. Матрицей нулевого оператора 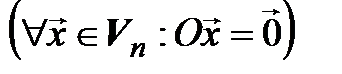в любом базисе является нулевая матрица; матрицей тождественного оператора 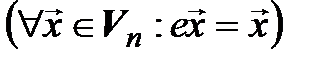также в любом базисе является матрица единичная.

2. Пусть 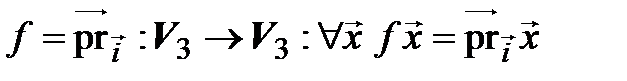. Составим матрицу оператора проектирования на ось Ox в базисе 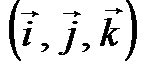. Для этого находим образы базисных векторов и разлагаем их по базису:

.

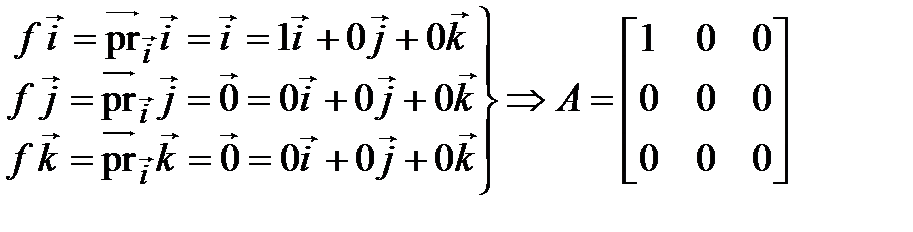3. Составим матрицу оператора 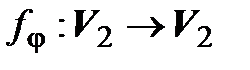поворота плоскости на угол 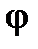(см. § 2) в базисе 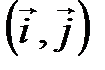. Из рис. 4.5 и 4.6 видно, что

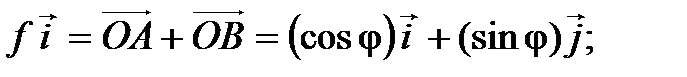
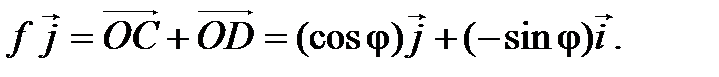
Тогда

.

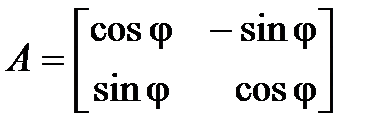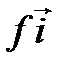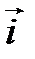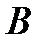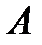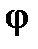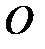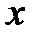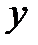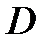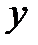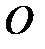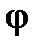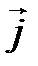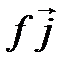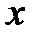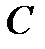Рис. 4.5 Рис. 4.6

Итак, если в пространстве 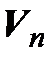задан какой-либо базис, то каждому линейному оператору 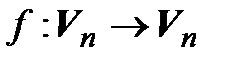можно поставить в соответствие его матрицу в этом базисе, т. е. квадратную матрицу A n-го порядка, причем эта матрица определяется однозначно.

Пусть теперь задана квадратная матрица А с элементами из поля P. Обозначим 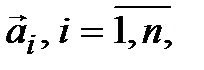вектор, координатный столбец которого в базисе (4.8) совпадает с i-м столбцом матрицы А. Получим упорядоченную систему векторов

( )

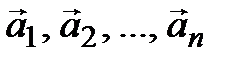Согласно теореме 4.1, существует единственный линейный оператор 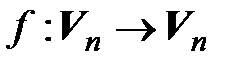такой, что 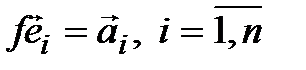. По определению матрица этого оператора в базисе (4.8) совпадает с А.

Обозначим 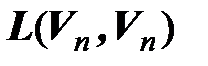– множество всех линейных операторов линейного пространства 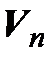над полем Р в себя. Из вышесказанного вытекает: если в 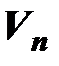задан базис, то определяется отображение

,

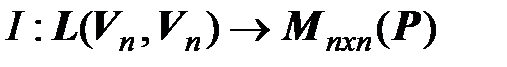которое ставит в соответствие каждому линейному оператору 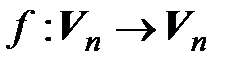его матрицу в этом базисе, причем это отображение взаимно однозначно. Это дает возможность в конечномерных линейных пространствах линейные операторы изучать с помощью их матриц.