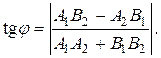Уравнение прямой, проходящей через две точки

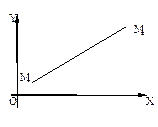Пусть на плоскости заданы две точки M₁(x₁,y₁), M₂(x₂,y₂). Для того чтобы написать уравнение прямой, проходящей через эти точки, полагаем в соответствующем уравнении прямой в пространстве 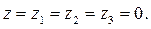Тогда получаем искомое уравнение в виде

.

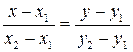Уравнение прямой, проходящей через данную точку в заданном направлении

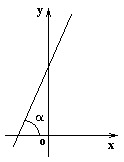Пусть прямая составляет угол a с осью OX. Угловым коэффициентом прямой k называется число .

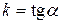Прямая может быть задана точкой М₁(x₁,y₁) и угловым коэффициентом k или двумя точками М₁(x₁,y₁) и М₂(x₂,y₂).

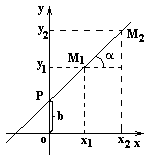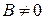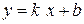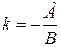Уравнение прямой с угловым коэффициентом k может быть получено из общего уравнения прямой Ax+By+C=0, если , тогда , где и 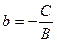. Прямая пересекает ось oy в точке P(0,b).

Из уравнения прямой, проходящей через две точки, имеем

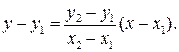
Отсюда 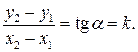Таким образом, 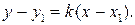Уравнение полученной прямой принимает вид уравнения прямой с угловым коэффициентом k, если b = y₁ - k x₁.

Уравнение прямой в отрезках

Общее уравнение прямой Ax+By+C=0 может быть преобразовано к виду уравнения прямой «в отрезках»: 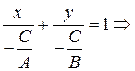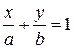. Прямая пересекает ось ox в точке А(а,0) и ось oy в точке В(0,b).

Нормальное уравнение прямой

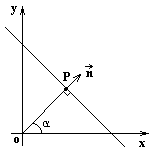Пусть известно расстояние от прямой до начала координат 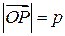и угол a между перпендикуляром к прямой и осью ox. Из нормального уравнения плоскости в пространстве, полагая z = 0 и учитывая, что

,

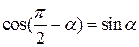получаем нормальное уравнение прямой на плоскости в виде:

.

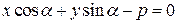Нормальное уравнение прямой можно получить из общего уравнения прямой Ax+By+C=0, умножив его на нормирующий множитель 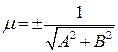. Знак числа m должен быть противоположен знаку числа С.

Косинусы углов, образуемых прямой с осями координат, называются направляющими косинусами прямой.

Если угол между прямой и осью ox равен a и угол между прямой и осью oy равен b, то .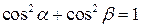

Расстояние от точки до прямой

Расстояние d от точки M₀(x₀,y₀) до прямой, задаваемой нормальным уравнением, равно модулю отклонения точки от прямой d, d = |d|,

где .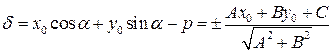

По этой формуле d положительно, если точка М₀ и начало координат лежат по разные стороны от прямой, в противном случае d отрицательно.

Координаты точки пересечения двух прямых

Если прямые заданы уравнениями A₁x+B₁y+C₁=0 и A₂x+B₂y+C₂=0, то координаты точки их пересечения (x₀, y₀) получаются как решение системы уравнений:

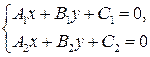
по формулам Крамера в виде:

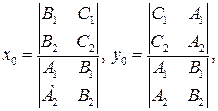при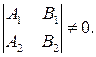

Угол между двумя прямыми

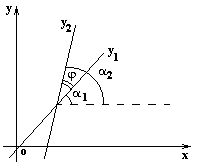Пусть две прямые заданы уравнениями:

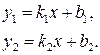
Острый угол j пересечения этих прямых (отсчитываемый против часовой стрелки) находится из следующих соотношений:

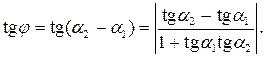
Отсюда .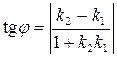

Если прямые заданы общими уравнениями А₁x+B₁y+C₁=0 и A₂x+B₂y+C₂=0, то угловые коэффициенты прямых равны: 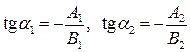и угол j между прямыми определяется формулой: