Электротехника и электроника

М и н и с т е р с т в о о б р а з о в а н и я и н а у к и

Р о с с и й с к о й Ф е д е р а ц и и

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

­­­­­­Национальный исследовательский ядерный университет

«МИФИ»

Волгодонский инженерно-технический институт – филиал

НИЯУ МИФИ

ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА

индивидуальное контрольное задание и

методические указания к его решению

Волгодонск 2012

Задача № 1

Для данной электрической схемы выполнить следующее:

1. Составить на основании законов Кирхгофа, систему уравнений для расчета токов во всех ветвях схемы.

2. Определить токи во всех ветвях схемы методом контурных токов.

3. Составить баланс мощностей.

4. Определить ток в n-ой ветви данной схемы методом эквивалентного генератора.

5. Начертить потенциальную диаграмму заданного контура.

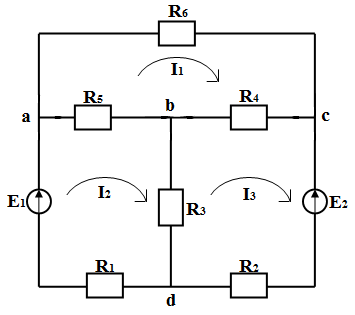
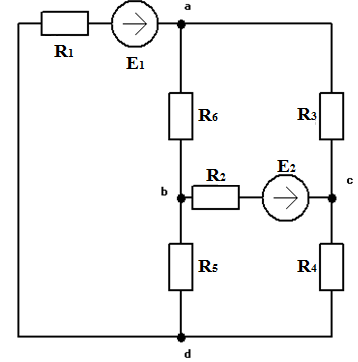Схема №1.

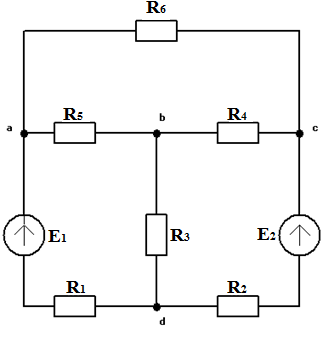Схема №2

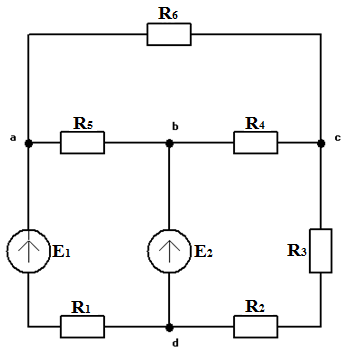Схема №3

Схема №4

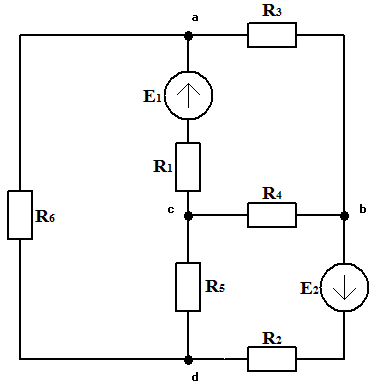
Группа №1.

№	Контур	E1	R1	E2	R2	R3	R4	R5	R6	n
	acba
	abdc
	acda
	abcda
	acbda
	abda		8,2
	acbda
	acba
	cbdc
	acda
	abcda
	acbda		9,5
	abda
	acbda		7,6
	acba
	cbda		4,5
	acda
	abcda
	acbda	19,5		7,5	13,5	10,5
	abda	19,5		7,5			16,5	22,5
	acbda					52,5
	acba		40,5		7,5				16,5
	cbdc			19,5		6,5			16,2
	acda	19,5	37,5					67,5	10,2
	abcda	10,5				13,5	22,5
	acbda
	abda
	acbda			16.5	17.5
	acba		55,5				7,5		16,5
	cbdc	19,5	37,5						10,2
	acda			10,5			7,5

Группа №2.

№	Контур	E1	R1	E2	R2	R3	R4	R5	R6	n
	acba	7,5		7,5
	abdc	3,5	7,5				4,5		3,5
	acda	6,5			17,5				7,5
	abcda	6,5			3,5
	acbda	10,5		2,5	5,5		3,5
	abda		4,5
	acbda			2,5				3,5
	acba		2,5		3,5			7,5
	cbdc
	acda
	abcda
	acbda
	abda	25,5
	acbda
	abda
	acba		3,5
	acda	6,5			3,5		2,5
	abcda	10,5
	acba		7,5
	cbdc	4,5
	acda
	abcda
	acbda
	abda
	acba		10,5				13,5
	dbcd					33,3
	abcda				10,5
	abda					7,5		10,5
	abcda
	abdca		7,5

Группа №3.

№	Контур	E1	R1	E2	R2	R3	R4	R5	R6	n
	acba	25,5
	abdc
	acda
	abcda
	acbda							22,5
	abda		10,5				13,5
	acbda
	acba
	cbdc
	acda
	abcda
	acbda			8,2
	abda
	acbda
	abda			9,5
	acba
	acda			7,6
	abcda
	acba			4,5
	cbdc
	acda
	cbdc		6,5		2,5	4,5	3,5
	abcda
	abda
	acbda								17,5
	acba
	cbdac
	acbda
	abcda	7,5			2,5			3,5
	abda			6,5

Группа №4.

№

Контур

n

E1

R1

E2

R2

R3

R4

R5

R6

acba

25.5

cbdc

acda

abcda

acbda

22.5

abda

10,5

13,5

acbda

acba

cbdc

acda

abcda

18

acbda

8,2

abda

acbda

abda

9,5

acba

acda

7,6

abcda

acba

4,5

cbdc

acda

cbdc

6,5

2,5

4,5

3,5

abcda

abda

acbda

17.5

acba

cbdac

acbda

abcda

7.5

2.5

3.5

abda

6.5

Задача № 2

Для данной электрической схемы выполнить следующее:

1. Составить, на основании законов Кирхгофа, систему уравнений для расчета токов во всех ветвях цепи и записать ее в дифференциальной и символической формах.

2. Определить комплексы действующих значений токов, воспользовавшись символическим методом расчета. Записать выражения для мгновенных значений токов.

3. Составить баланс мощностей в комплексной форме, выполнив соответствующие вычисления.

4. Построить на комплексной плоскости векторную диаграмму напряжений и токов.

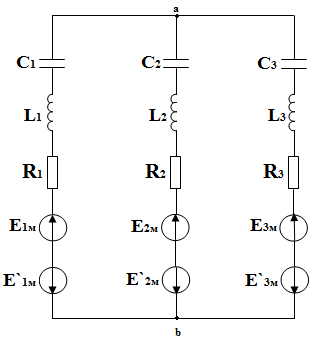
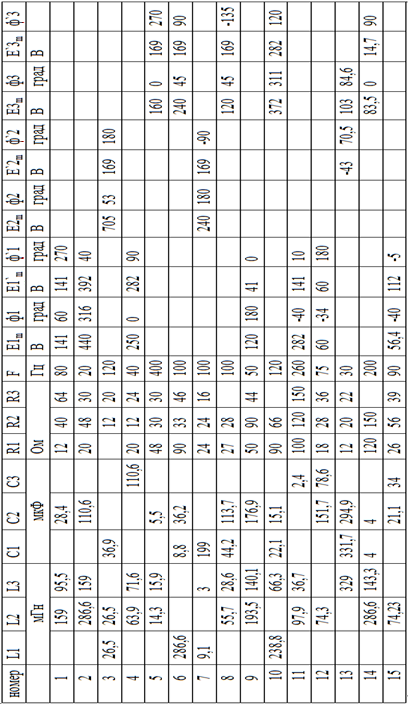
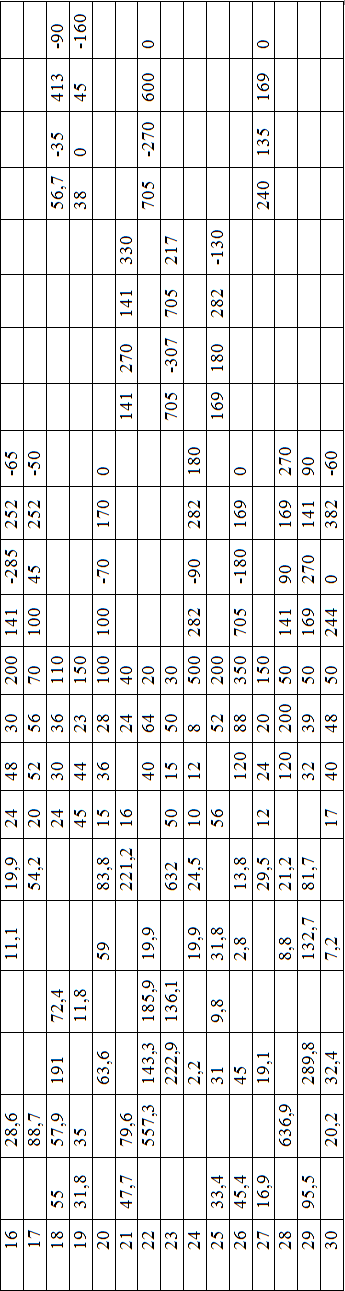
Задача №3.

В трехфазной системе нагрузка соединена в звезду с нейтральным проводом. Определить:

1. Фазные и линейные токи.

2. Угол сдвига фаз между тока и напряжением в каждой фазе.

3. Активную, реактивную и полную мощность потребляемую системой.

При обрыве фазы А определить режимы в остальных двух фазах при наличие нейтрального провода и без него.

Для всех случаев построить векторные диаграммы.

№ вариант	UФ	RФ	XLФ	ХСФ	№ вариант	UФ	RФ	XLФ	ХСФ

Задача № 1

Для данной электрической схемы выполнить следующее:

1. Составить на основании законов Кирхгофа, систему уравнений для расчета токов во всех ветвях схемы.

2. Определить токи во всех ветвях схемы методом контурных токов.

3. Составить баланс мощностей.

4.Определить ток в n-ой ветви данной схемы методом эквивалентного генератора.

5. Начертить потенциальную диаграмму заданного контура.

Контур	E1	R1	E2	R2	R3	R4	R5	R6	n
acda

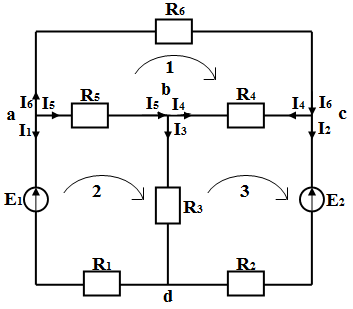Схема№2

1) Составим уравнения по законам Кирхгофа.
Первый закон:
Алгебраическая сумма токов в любом узле электрической цепи равна нулю:

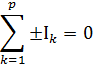
где p-число ветвей сходящихся в данном узле.
Для заданной цепи составим соответственно уравнения для узлов a,b,c .

Второй закон:
Алгебраическая сумма падений напряжения, вдоль замкнутого контура цепи, равна алгебраической сумме ЭДС в этом контуре.

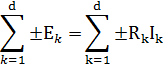
где d-число ветвей в контуре.

Число уравнений по второму закону Кирхгофа равно количеству независимых контуров. Независимым называется контур, в который входит хотя бы одна ветвь не входящая в другие контуры. Если в цепи m-ветвей и n-узлов, то по первому закону Кирхгофа может быть составлено (n-1) уравнений, а по 2му закону (m-(n-1)) уравнений.

Таким образом, количество уравнений в системе, составленной по законам Кирхгофа, равно числу ветвей в электрической цепи.

-I₆-I₁-I₅=0

I₅-I₄-I₃=0

I₆-I₂-I₄=0

I₆R₆-I₄R₄-I₅R₅=0

I₃R₃-I₁R₁+I₅R₅=E₁

I₂R₂-I₃R₃+I₄R₄=-E₂

Метод контурных токов

позволяет сократить количество уравнений до числа независимых контуров.

Последовательность расчета такова:
1.Задаёмся произвольным направлением контурных токов.
2.Для контуров определяем собственные и взаимные сопротивления

Собственное сопротивление контура – сумма сопротивлений, входящих в контур.

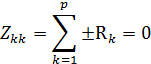
где p – число ветвей в контуре.

Z₁₁=R₆+R₄+R₅=42 Ом
Z₂₂=R₁+R₅+R₃=46 Ом
Z₃₃=R₃+R₂+R₄=60 Ом

Взаимные сопротивления – это сопротивления смежных ветвей взятых со знаком «+», если направление контурных токов в этой ветви совпадают.

Z₁₂ – взаимное сопротивление 1 и 2 контуров;

Z₂₃ – взаимное сопротивление 2 и 3 контуров;

Z₃₁ – взаимное сопротивление 3 и 1 контуров
Z₁₂= - R₅=-18; Z₂₃= R₃=20; Z₃₁= R₄=14

3. Составим уравнения для независимых контуров по второму закону Кирхгофа.

I_11*Z₁₁-I_22*Z₁₂-I_33*Z₃₁=0
-I_11*Z₁₂+I_22*Z₁₂-I_33*Z₂₃=E₁
-I_11*Z₃₁-I_22*Z₂₃-I_33*Z₃₁=-E₂

Подставив численные значения, получим:

42I₁₁ - 18I₂₂ -14I₃₃ =0
-18I₁₁ +46I₂₂ -20I₃₃ =20
-14I₁₁ -20I₂₂ +60I₃₃ = -24

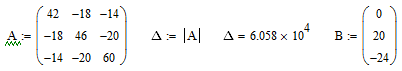Решаем систему уравнений методом Крамера.
Составим матрицу системы и найдем ее определитель:

Определитель не равен нулю – система имеет единственное решение.
Найдем остальные определители системы, заменяя свободными членами коэффициенты при соответствующих неизвестных.

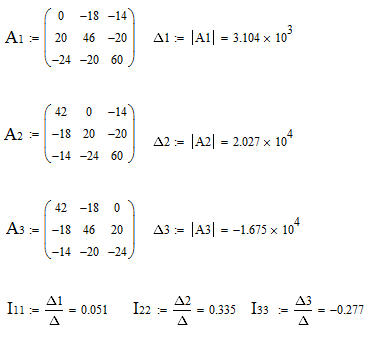
Получаем:

I₁₁= 0.051А I₂₂=0.335А I₃₃=0.277А

4.Определяем истинные токи в ветвях.

В ветвях принадлежащих одному контуру величина тока равна соответствующему контурному току, а его направление выбирается таким, чтобы ток был положительным.

В смежных ветвях ток равен алгебраической сумме смежных контурных токов, а направление выбирается так, чтобы ток был положительным.

I₁=I₂₂=0.335A; I₂=-I₃₃=0.277A; I₃=I₂₂-I₃₃=0.612A;

I₄=I₁₁-I₃₃=0.334A; I₅=I₂₂- I₁₁=0.284A; I₆=I₁₁=0.051A.