Практическая работа 12. Статистические расчеты средствами Excel

Вычисление статистических характеристик

В Excel имеется несколько способов вычисления статистических характеристик:

- по формулам;

- с помощью статистических функций;

- с помощью надстройки Пакет анализа.

Таблица 3

Статистическая величина	Формула	Функция
Сумма		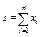СУММ()
Среднее арифметическое		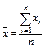Срзнач()
Среднее линейное отклонение		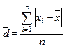Сроткл()
Дисперсия по генеральной совокупности		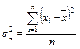Диспр()
Дисперсия по выборке		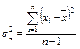Дисп()
Среднее квадратичное отклонение		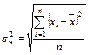Стандотклонп()
Смещенное среднее отклонение (по выборке)		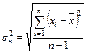Стандотклон()

В таблице 3 приведены формулы и соответствующие им функции для вычисления некоторых статистических характеристик.

Кроме того, имеются функции для вычисления следующих статистических характеристик:

- количество значений – СЧЕТ();

- максимум ‑ Макс();

- минимум ‑ Мин();

- мода ‑ Мода();

- медиана ‑ Медиана().

Чтобы воспользоваться надстройкой Пакет анализа, надо:

1. На вкладке Данные в группе Анализ выбрать команду Анализ данных.

2. В открывшемся диалоговом окне выбрать строку Описательная статистика.

3. В поле Входной интервал указать диапазон данных, для которых надо получить статистические оценки.

4. Если диапазон данных выделен вместе с заголовком, установить флажок Метки в первой строке;

5. Выбрать вариант размещения выходных данных: текущий рабочий лист, новый рабочий лист или новая рабочая книга.

В случае размещения выходных данных на текущем листе включить режим Выходной интервал и указать левую верхнюю ячейку диапазона, в который должны быть выведены результаты.

6. Установить флажок Итоговая статистика.

7. Щелкнуть по кнопке ОК.

Экстраполяция

Экстраполяция – это прогнозирование неизвестных значений путем продолжения функции за границы области известных значений.

Экстраполяцию динамического ряда в Excel можно выполнить различными способами.

I способ – про помощи операции автозаполнения:

1. Выделить ряд данных.

2. Правой кнопкой мыши протащить маркер заполнения на нужное количество ячеек.

3. В открывшемся контекстном меню выбрать нужный пункт:

- Линейное приближение – для заполнения ячеек значениями, вычисленными на основе аппроксимации исходных данных линейной функцией;

- Экспоненциальное приближение ‑ для заполнения ячеек значениями, вычисленными на основе аппроксимации исходных данных экспоненциальной функцией;

- Прогрессия – заполнение ячеек арифметической или геометрической прогрессией.

II способ – про помощи встроенных функций:

- ПРЕДСКАЗ() – линейная экстраполяция для отдельной точки;

- ТЕНДЕНЦИЯ() – линейная экстраполяция для массива точек;

- РОСТ() – экспоненциальная экстраполяция для массива точек.

Построение линии тренда

Линия тренда – графическое представление направления изменения данных в ряде данных. Линии тренда используются при прогнозировании.

Для построения на диаграмме линии тренда надо:

1. Щелкнуть правой кнопкой мыши по любому маркеру диаграммы.

2. В открывшемся контекстном меню выбрать команду Добавить линию тренда;

3. В открывшемся диалоговом окне на вкладке Параметры линии тренда в группе Построение линии тренда выбрать нужный вариант: экспоненциальная, линейная, логарифмическая, полиномиальная, степенная и т.д.

4. В группе Прогноз указать, на сколько периодов вперед и (или) назад надо выполнить прогноз.

5. При необходимости установить флажок Показывать уравнение на диаграмме.

6. При необходимости изменить форматы линии на вкладках Тип линии, Цвет линии и Тень.

7. Закрыть диалоговое окно.

Корреляционно-регрессионный анализ

Целью корреляционно-регрессионного анализа является изучение зависимостей между двумя или несколькими показателями.

Корреляция характеризует тесноту связи между случайными величинами. Если коэффициент корреляции равен +1 или -1, то связь считается функциональной, Если коэффициент корреляции равен 0, считается, что связь отсутствует.

Различают парную корреляцию, когда исследуется зависимость показателя от одного параметра, и множественную корреляцию, когда показатель зависит от нескольких параметров.

Для определения коэффициента парной корреляции в Excel предназначена функция КОРРЕЛ(), аргументами которой являются массивы значений случайных величин.

Коэффициент корреляции можно определить с помощью надстройки Пакет анализа:

1. На вкладке Данные в группе Анализ выбрать команду Анализ данных.

2. В открывшемся диалоговом окне выбрать строку Корреляция.

3. В открывшемся диалоговом окне:

- указать входной интервал;

- выбрать способ группирования данных: по строкам или по столбца;

- указать левую верхнюю ячейку выходного интервала.

4. Щелкнуть по кнопке ОК.

Регрессионный анализ предназначен для выявления аналитической зависимости между показателями, т.е. для нахождения уравнения регрессии.

Для нахождения уравнения регрессии в Excel предназначена функция ЛИНЕЙН(). С помощью этой функции вычисляются коэффициенты уравнения прямой, которая наилучшим образом аппроксимирует имеющиеся данные.

В случае n переменных уравнение регрессии имеет вид

.

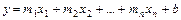Функция ЛИНЕЙН() возвращает массив коэффициентов 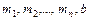. Аргументами функции являются массив значений y и массив значений переменных .

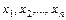Если y есть функция одной переменной, то массивы значений x и y могут иметь любую форму (один столбец, одна строка, несколько столбцов и строк) при условии, что они имеют одинаковую размерность.

Если y есть функция нескольких переменных, то массив значений y должен быть одномерным, т.е. занимать один столбец (или одну строку), а массив значений x должен занимать несколько столбцов (или строк), при этом каждый столбец (или строка) будут интерпретироваться как отдельная переменная.

Кроме того, функция ЛИНЕЙН() имеет логический аргумент Конст, который определяет значение свободного члена b: если Конст=ЛОЖЬ, то полагается b=0.

Функция ЛИНЕЙН() может также возвращать дополнительную регрессионную статистику. Для этого надо присвоить логическому аргументу Статистика значение ИСТИНА.

Поскольку функция ЛИНЕЙН() возвращает массив значений, поэтому перед вводом формулы надо выделить n+1 ячейку, а закончить ввод формулы – нажатием клавиш Ctrl+Shift+Enter.

Коэффициенты уравнения регрессии и регрессионную статистику можно получить с помощью надстройки Пакет анализа:

1. На вкладке Данные в группе Анализ выбрать команду Анализ данных.

2. В открывшемся диалоговом окне выбрать строку Регрессия.

3. В открывшемся диалоговом окне:

- указать входной интервал значений y;

- указать входной интервал значений x;

- выбрать способ вычисления константы b (0: да или нет);

- указать левую верхнюю ячейку выходного интервала.

4. Щелкнуть по кнопке ОК.

Частотный анализ

Распределение частот в Excel можно создать несколькими способами:

- с помощью функции ЧАСТОТА();

- с использованием надстройки Пакет анализа;

- с помощью сводных таблиц.

Функция ЧАСТОТА() возвращает количество значений из диапазона данных, попадающих в каждый интервал группировки.

Аргументами этой функции являются массив данных и массив интервалов группировки.

Массив верхних границ интервалов группировки можно определить по формуле:

=МИН(массив)+{1:2:…:n}*(МАКС(массив)-МИН(массив))/n

Здесь массив – диапазон данных; n – количество интервалов группировки.

Формула массива верхних границ и функция ЧАСТОТА() возвращают массив ячеек, поэтому перед их вводом надо выделить столбец из n ячеек, а закончить ввод– нажатием клавиш Ctrl+Shift+Enter.

Чтобы создать распределение частот с помощью надстройки Пакет анализа, надо:

1. На вкладке Данные в группе Анализ выбрать команду Анализ данных.

2. В открывшемся диалоговом окне выбрать строку Гистограмма.

3. В открывшемся диалоговом окне:

- в поле Входной интервал указать диапазон данных;

- в поле Интервал карманов указать массив верхних границ интервалов;

- в поле Выходной интервал указать левую верхнюю ячейку выходного интервала;

- для графического отображения распределения частот (гистограммы) установить флажок Вывод графика.

4. Щелкнуть по кнопке ОК.

Распределение частот можно получить, создав сводную таблицу с группировкой по полю, содержащему числовые данные. При этом в качестве начального значения задается минимальное значение диапазона, конечного значения – максимальное, шага – интервал группировки, равный (МАКС(массив)-МИН(массив))/n.

Практическое задание. Вычисление статистических характеристик

1. Ввести данные из таблицы 4.

2. Вычислить следующие статистические характеристики ряда данных:

- количество значений;

- сумма;

- максимум;

- минимум;

- среднее арифметическое;

- среднее линейно отклонение;

Таблица 4

- дисперсия по генеральной совокупности;

Месяц	Цена
Январь 2009	8,0
Февраль 2009	8,5
Март 2009	8,0
Апрель 2009	8,5
Май 2009	9,0
Июнь 2009	10,0
Июль 2009	9,5
Август 2009	10,0
Сентябрь 2009	10,5
Октябрь 2009	10,5
Ноябрь 2009	10,5
Декабрь 2009	11,0

- дисперсия по выборке;

- среднее квадратичное отклонение;

- смещенное среднее квадратичное отклонение (по выборке);

- мода;

- медиана.

Вычисления произвести тремя способами: по формулам, с помощью стандартных функций; с помощью надстройки Пакет анализа.

Указание: для расчетов по формулам добавить к таблице данных столбцы для вычисления отклонений 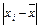и квадратов отклонений.

Экстраполяция

3. На новый лист поместить копию столбца Месяц и шесть копий столбца Цена. Дать новые названия столбцам: Линейное приближение, Предсказание, Тенденция, Экспоненциальное приближение, Рост, Геометрическая прогрессия. Над первыми тремя столбцами ввести общее название Линейная экстраполяция, над последними тремя столбцами – Экспоненциальная экстраполяция.

4. Используя маркер заполнения, дополнить столбец Месяц датами до июня 2010 г.

5. Выполнить линейную экстраполяцию, используя операцию автозаполнения. Для этого следует:

- выделить значения столбца Линейное приближение (без заголовка);

- протащить маркер заполнения правой на шесть ячеек вниз кнопкой мыши;

- в открывшемся контекстном меню выбрать пункт Линейное приближение.

6. Выполнить экспоненциальную экстраполяцию, используя операцию автозаполнения и пункт контекстного меню Экспоненциальное приближение (использовать данные соответствующего столбца).

7. Выполнить линейную экстраполяцию при помощи функции ПРЕДСКАЗ():

- установить курсор в ячейке столбца Предсказание, соответствующей дате «Январь 2010», вызвать функцию ПРЕДСКАЗ();

- в поле X указать ячейку с датой «Январь 2010»;

- в поле Известные значения x –диапазон ячеек столбцаМесяц с датами от января 2009 до декабря 2009 (абсолютные ссылки);

- в поле Известные значения y –диапазон ячеек столбцаПредсказание, соответствующий датам от января 2009 до декабря 2009 (абсолютные ссылки);

- скопировать формулу в остальные ячейки столбца Предсказание

8. Выполнить линейную экстраполяцию при помощи функции ТЕНДЕНЦИЯ():

- выделить ячейки столбца Тенденция, соответствующие датам от января 2010 до июня 2010;

- вызвать функцию ТЕНДЕНЦИЯ();

- в поле Известные значения y указатьдиапазон ячеек столбцаТенденция, соответствующий датам от января 2009 до декабря 2009;

- в поле Известные значения x ‑диапазон ячеек столбцаМесяц с датами от января 2009 до декабря 2009;

- в поле Новые значения x ‑диапазон ячеек столбцаМесяц с датами от января 2010 до июня 2010;

- нажать клавиши Ctrl + Shift + Enter.

9. Выполнить экспоненциальную экстраполяцию при помощи функции РОСТ() (аргументы этой функции такие же, как и у функции ТЕНДЕНЦИЯ).

10. Выполнить экстраполяцию, используя операцию автозаполнения и пункт контекстного меню Прогрессия (геометрическая прогрессия с автоматическим определением шага).

Построение линии тренда

11. На отдельном листе построить диаграмму, отображающую изменение цены за период с января по декабрь 2009 г.: в качестве категорий использовать данные из столбца Месяц, в качестве ряда – данные из столбца Цена.

12. Построить линии тренда различных типов: экспоненциальную, линейную, логарифмическую, полиномиальную, степенную. Сделать прогноз на 6 периодов вперед. Задать показ уравнений линий тренда. Задать разные цвета для линий.

Корреляционно-регрессионный анализ

13. Ввести данные из таблицы 5.

Значения столбца Себестоимость рассчитываются как сумма всех видов затрат;Наценка = Цена – Себестоимость.

14. Используя функцию КОРРЕЛ(), вычислить коэффициенты парной корреляции между ценой и себестоимостью.

15. При помощи функции ЛИНЕЙН() вычислить коэффициенты m и b уравнения регрессии y=mx+b, показывающего зависимость цены от себестоимости (эта функция возвращает массив из двух ячеек, поэтому перед вводом формулы надо выделить две ячейки, а закончить ввод формулы – нажатием клавиш Ctrl+Shift+Enter).

16. При помощи функции ЛИНЕЙН() вычислить коэффициенты m и b уравнения регрессии y=mx+b, показывающего зависимость цены от наценки.

17. При помощи функции ЛИНЕЙН() вычислить коэффициенты m₁, m₂, m₃, m₄, m₅, m₆ и b уравнения регрессии

y=m₁x₁+m₂x₂+m₃x₃+m₄x₄+m₅x₅+m₆x₆+b,

показывающего зависимость цены от всех видов затрат (эта функция возвращает массив из семи ячеек).

Таблица 5

Товар	Цена	Материальные затраты	Затраты на оплату труда	Транспортные расходы	Амортизация	Реклама	Прочие расходы	Себестоимость	Наценка
Тов.1
Тов.2
Тов.3
Тов.4
Тов.5
Тов.6
Тов.7
Тов.8
Тов.9
Тов.10

18. Выполнить корреляционно-регрессионный анализ зависимости цены от себестоимости, цены от наценки и цены от всех видов затрат, используя надстройку Пакет анализа.

Частотный анализ

19. Ввести данные из таблицы 6.

20. Определить параметры группировки:

- максимум = максимальное значение интервала;

- минимум = минимальное значение интервала;

- размах вариации = максимум ‑ минимум;

- количество интервалов = 4;

- интервал группировки = размах вариации / количество интервалов.

21. Выполнить частотный анализ при помощи функции ЧАСТОТА(). Для этого оставить таблицу со столбцами

№ группы – номера по порядку от 1 до 4;

Верхняя граница= МИН(массив)+{1:2:3:4}*(МАКС(массив)-МИН(массив))/4;

Число банков – использовать функцию ЧАСТОТА().

Таблица 6

№ банка	Уставный капитал

Аргументы функции ЧАСТОТА():

Массив данных – интервал ячеек столбца Уставный капитал;

Массив интервалов – интервал ячеек столбца Верхняя граница.

22. Построить гистограмму: в качестве ряда использовать значения столбца Число банков, в качестве категорий – значения столбца Верхняя граница.

23. На гистограмме построить линию тренда экспоненциального типа, показать уравнение на диаграмме.

24. Провести частотный анализ при помощи надстройки Пакет анализа:

- в качестве входного интервала указать интервал ячеек столбца Уставный капитал;

- в качестве интервала карманов указать интервал ячеек столбца Верхняя граница;

- в качестве выходного интервала указать левую верхнюю ячейку диапазона, куда должны быть выведены результаты;

- установить флажок Вывод графика.

25. Повторить частотный анализ при помощи надстройки Пакет анализа, но не указывать интервал карманов (в этом случае он будет сформирован автоматически). Сравнить результаты.

26. Выполнить частотный анализ, используя сводную таблицу: в область Названия строк поместить поле Уставный капитал, в область Значения – поле № банка, выбрать операцию Количество. Провести группировку по полю Уставный капитал, в качестве начального и конечного значений задать соответственно минимальное и максимальное значение поле Уставный капитал, в качестве шага – интервал группировки, равный (МАКС(Уставный капитал)-МИН(Уставный капитал))/4.

Построить сводную диаграмму. Для этого выделить любую ячейку в сводной таблице и на вкладке Работа со сводными таблицами – Параметры в группе Сервис выбрать команду Сводная диаграмма