Теорема о сложении ускорений (теорема кориолиса)

Найдем зависимость между относительным, переносным и абсолютным ускорениями точки. Из равенства (84) получим

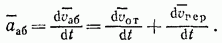
Производные здесь определяют изменение каждого из векторов при абсолютном движении. Эти изменения слагаются в общем случае из изменений при относительном и при переносном движениях, что ниже будет непосредственно показано. Следовательно, если условиться изменения, которые векторы и получают при относительном движении, отмечать индексом «1», а при переносном движении — индексом «2», то равенство (85) примет вид

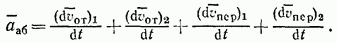
Но по определению (см. § 64, п. 1) относительное ускорение характеризует изменение относительной скорости только при относительном движении; движение осей 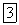, т. е. переносное движение при этом во внимание не принимается. Поэтому

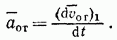
В свою очередь, переносное ускорение характеризует изменение переносной скорости только при переносном движении, так как (см. § 64, п. 2), где m — точка, неизменно связанная с осями и, следовательно, получающая ускорение только при движении вместе с этими осями, т. е. при переносном движении. Поэтому

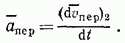
В результате из равенства (86) получим

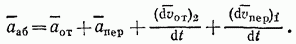
Введем обозначение

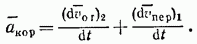
Величина акор, характеризующая изменение относительной скорости точки при переносном движении и переносной скорости точки при ее относительном движении, называется поворотным, или кориолисовым, ускорением точки. В результате равенство (89) примет вид

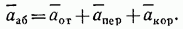
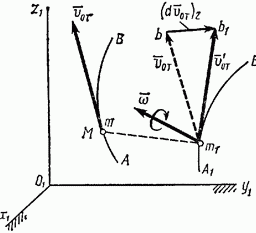
Рис. 188

Формула (91) выражает следующую теорему Кориолиса о сложении ускорений: при сложном движении ускорение точки равно геометрической сумме трех ускорений: относительного, переносного и поворотного, или кориолисова.

Найдем для вычисления акор формулу, вытекающую из равенства (90). При этом, рассматривая общий случай, будем считать переносное движение, т. е. движение подвижных осей , а с ними и кривой АВ (см. рис. 182), слагающимся из поступательного движения вместе с некоторым полюсом и вращения вокруг этого полюса с угловой скоростью , называемой переносной угловой скоростью. Величина , как показано от выбора полюса не зависит и на изображенных рис. 188, где полюс точка , и рис. 189, где полюс О, имеет одно и то же значение.

Начнем с определения При рассматриваемом переносном движении вектор направленный по касательной к кривой АВ, переместится вместе с этой кривой поступательно (придет в положение рис. 188) и одновременно повернется вокруг точки до положения . В результате вектор получит в переносном движении приращение где — скорость, с которой перемещается точка b при повороте вектора вокруг точки Так как этот поворот происходит с угловой скоростью , то по формуле . В результате получаем и

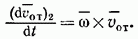
Теперь определим Скорость равна скорости той неизменно связанной с подвижными осями точки кривой АВ, с которой в данный момент времени совпадает точка М (рис. 189). Если точку О принять за полюс и обозначить через вектор то по формуле (81)

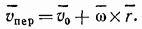
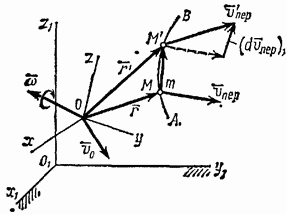
Рис. 189

Совершив за промежуток времени относительное перемещение точка придет в положение , для которого и

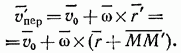
Следовательно, вследствие того, что точка совершает относительное перемещение вектор ипер получает приращение

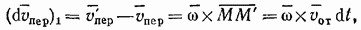
откуда

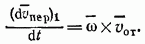
Подставляя величины (92) и (93) в равенство (90), получим

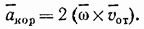
Таким образом, кориолисово ускорение равно удвоенному векторному произведению переносной угловой скорости (угловой скорости подвижной системы отсчета) на относительную скорость точки.

Случай поступательного переносного движения. В этом случае и, следовательно, . В результате равенство (91) дает

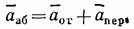
т. е. при поступательном переносном движении абсолютное ускорение точки равно геометрической сумме относительного и переносного ускорений.

Результат здесь аналогичен тому, который дает теорема о сложении скоростей.

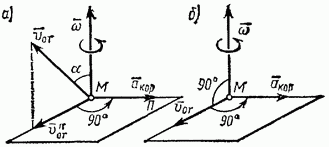
Рис. 190

Вычисление относительного, переносного и кориолисова ускорений. Относительное ускорение, поскольку при его нахождении движение подвижных осей во внимание не принимается, вычисляется обычными методами кинематики точки (§ 40, 43). Переносное ускорение вычисляется как ускорение точки, неизменно связанной с подвижными осями, т. е. как ускорение точки некоторого твердого тела, по формулам, полученным для ускорений точек твердого тела в § 51, 58, 62, 63. Кориолисово ускорение вычисляется по формуле (94). Модуль кориолисова ускорения, если угол между векторами обозначить через а, будет равен

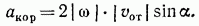
Направлен вектор акор так же, как и вектор перпендикулярно плоскости, проходящей через векторы в ту сторону, откуда кратчайшее совмещение со с видно происходящим против хода часовой стрелки (рис. 190, а).

Из рис. 190, а видно также, что направление вектора акор можно определить, спроектировав вектор на плоскость П, перпендикулярную , и повернув эту проекцию на 90° в сторону переносного вращения.

Если относительная траектория — плоская кривая и перемещается все время в своей плоскости, то угол (рис. 190, б) этом случае по модулю

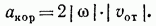
Кроме того, как видно из рис. 190, б, направление акпр можно в этом случае найти, повернув вектор относительной скорости на 90° в сторону переносного вращения (т. е. по ходу или против часовой стрелки, в зависимости от направления вращения).

На рис. 191 для иллюстрации приведенных правил показано направление кориолисова ускорения шарика М, движущегося вдоль трубки АВ в случаях, когда трубка вращается в плоскости чертежа (рис. 191, а) и когда она при вращении описывает конус (рис. 191, б).

Из формулы (96) видно, что кориолисово ускорение может обращаться в нуль в следующих случаях;

1) когда т. е. когда переносное движение является поступательным [формула (95)] или если переносная угловая скорость в данный момент времени обращается в нуль;

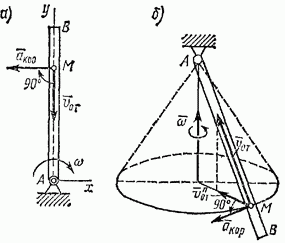
Рис. 191

2) когда т. е. когда относительная скорость в данный момент времени обращается в нуль;

3) когда или т. е. когда относительное движение происходит по направлению, параллельному оси переносного вращения, или если в данный момент времени вектор параллелен этой оси.

2 Геометрическим условием равновесия твердого тела, находящегося под действием сходящейся системы сил F₁ + F₂ + ... + F_n является замкнутость силового многоугольника, т. е. начало первого вектора F₁ должно совпадать с концом последнего F_n.

Аналитические условия равновесия. При равновесии системы сил модуль равнодействующей R = [R_х² + R_у²]^1/2 = 0, поэтому R_х = SF_kх = 0, R_у = SF_ky = 0

Экзаменационный билет № 17

1. Теорема о проекциях скоростей двух точек плоской фигуры.

2. Момент силы относительно центра. Свойства моментов сил.

3. Задача.