Понятие о разрешимости уравнений в радикалах

Поле алгебраических чисел и его замкнутость

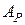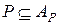Обозначим через – множество всех чисел, алгебраических относительно поля . Ясно, что , точно также любое простое ( а, следовательно, и составное ) алгебраическое расширение поля является подмножеством множества .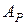

Теорема 1. Множество 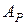всех чисел, алгебраических относительно поля , является подполем поля .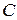

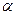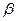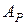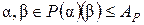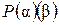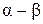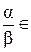
Доказательство. Пусть и - любые элементы множества . Так как и является полем , что , 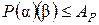Это значит, что 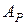замкнуто относительно вычитания и деления, т.е. подполем поля .

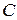Определение. Множество всех чисел, алгебраических относительно поля , называется полем алгебраических чисел над полем . Если 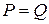, то это множество называют просто полем алгебраических чисел.

Теорема 3. Если над полем существует неприводимый многочлен любой степени ( как, например, над полем 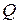), то поле 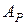алгебраических над полем чисел не является конечным расширением поля .

Действительно, предположим, что 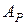является конечным расширением поля степени 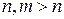. Точка для любого числа 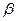из 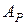система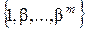 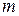линейно зависима в 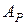над и, следовательно, степень 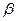не превышает 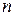. Но это означает, что все многочлены степени 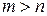приводимы в кольце 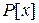: получили противоречие.

Следствие. Поле алгебраических чисел – бесконечномерное пространство над полем 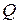. Если же над полем существуют неприводимые многочлены степени 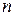, а все многочлены степени 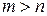приводимы, то этого утверждать уже нельзя. Например, поле 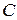является полем алгебраических чисел над полем 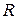. В тоже время 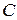– простое алгебраическое расширение поля 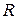( 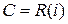), причем размерность 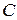над полем 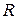равна 2.

Теорема 2. Поле 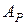алгебраических над полем чисел алгебраически замкнуто, т.е. все корни многочлена степени 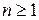из кольца 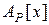принадлежат полю .

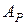Доказательство. Пусть 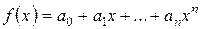– любой многочлен из кольца 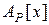, 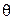- любой корень этого многочлена. Требуется доказать, что .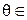

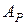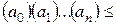
Очевидно, что 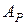, а число 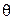- алгебраично над полем 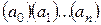. Но тогда 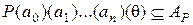и, следовательно, .

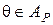Заметим, что здесь использовался тот факт, что при определении составного алгебраического расширения не требуется алгебраичность 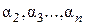над полем .

В связи с теоремой 2 полезно подчеркнуть, что 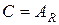, а алгебраическая замкнутость поля 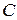доказывалась и ранее – она вытекает из основной теоремы алгебры.

Упражнения.

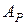1. Привести пример такого поля , что поле алгебраично над полем чисел является конечным расширением поля .

2. Доказать: если 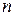– наивысшая степень неприводимых в кольце 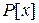многочленов, то 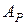является конечным расширением поля степени .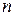

3. Доказать, что поле алгебраических чисел счетно.

Понятие о разрешимости уравнений в радикалах.

Определение 1. Говорят, что число 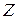выражается в радикалах (в квадратных радикалах) через числовое множество 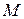, если 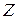можно представить через элементы множества 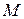с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операций извлечения корня (квадратного корня).

Например, число 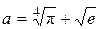, где имеются в виду арифметические корни, выражается в радикалах через множество 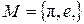. Так как это число представлено в виде 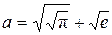, то оно выражается даже в квадратных радикалах через множество .

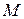Заметим, что операция извлечения корня неоднозначна и поэтому разные числа могут одинаково выражаться в радикалах через одно и тоже множество

Например, все три корня кубического уравнения 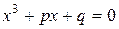одинаково выражаются в радикалах через коэффициенты по формуле Кардано.

Укажем некоторые свойства понятия выражения в радикалах.

1. Всякое число из множества 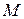выражается в радикалах множество 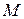. Например, число 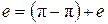выражается в радикалах через множество .

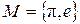2. Каждое рациональное выражается в радикалах через любое множество .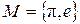

Например, число 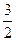выражается через множество 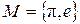в виде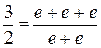

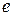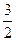Заметим, что в выражении чисел и через множество 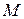операция извлечения корня не используется. В таких случаях говорят, что число выражается через множество 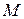рационально.

3. Если 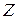выражается в радикалах через множество 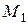, а каждый элемент из 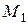, выражается в радикалах через множеств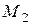о , то 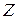– выражается в радикалах через .

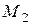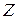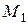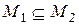4. Если выражается в радикалах через множество и , то 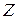выражается в радикалах через .

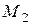5. Число 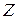выражается в радикалах через конечное множество 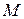тогда и только тогда, когда 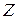выражается в радикалах через поле .

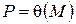Свойства 1-4 очевидны, докажем свойство 5.

Если 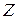выражается в радикалах через множество 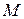, то тоже в силу свойства 4 выражается в радикалах и через множество 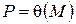, содержащее подмножество 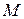. Обратно, пусть 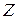выражается в радикалах через поле 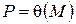. Согласно теореме 2 §6 и свойству 2 каждый элемент из поля выражается в радикалах (и даже рационально) через множество 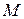. Но тогда по свойству 3 и число 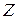выражается в радикалах через множество .

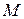Свойства 1-5 будут справедливы и в том случае, когда всюду слово « выражается в радикалах» заменить словами « выражается в квадратных радикалах»

Напомним, что поле 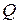является подполем любого числового поля. Поэтому составное расширение можно определить и иначе: это есть пересечение всех числовых полей, содержащих подмножество .

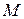Определение 2. Уравнение

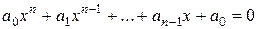(1)

называется разрешимым в радикалах (в квадратных радикалах) если каждый корень этого уравнения выражается в радикалах (в квадратных радикалах) через множество .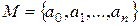

Определение 3.Составное расширение 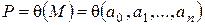называется областью рациональности уравнения (1).

Из свойства 5 вытекает следующая теорема.

Теорема 1. Уравнение (1) разрешимо в радикалах (в квадратных радикалах) тогда и только тогда, когда каждый корень этого уравнения выражается в радикалах (в квадратных радикалах) через область рациональности этого уравнения.

Ясно, что линейные, квадратные и биквадратные уравнения разрешимы только в радикалах, но и в квадратных радикалах. Уравнения 3 и 4-ой степени разрешимы в радикалах, но не всегда разрешимы в квадратных радикалах. Вопрос о разрешимости в радикалах уравнений выше 4-й степени оказался весьма трудным. Только в начале ХХ1 века норвежский математик Н.АБЕЛЬ (1802-1829 г.г.) установил, что для уравнения 5 степени не существует формулы, подобной формуле КАРДАНА для уравнений 3-ей степени, которая бы выражала корни данного уравнения через коэффициенты. Значительно дальше продвинулся в этом направлении французский математик Э.ГАЛУА (1811-1832г.г.) Используя понятие группы, он исследовал условия разрешимости в радикалах уравнений выше 4-ой степени.