Матриця як таблиця

Матриця - це сукупність чисел або об'єктів іншої природи, розташованих у виді прямокутної таблиці:

A =			…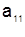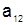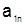
		…
…	…	…	…
		…

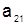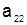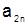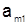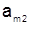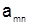Така таблиця, що складається з т рядків і п стовпців, містить тп кліток (позицій). При цьому говорять, що матриця має розмір 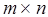і її називають 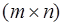матрицею. Позицію на перетині i-го рядка і j-го стовпця будемо називати ij-кліткою. Числа або будь-які інші об'єкти, розташовані в клітках таблиці, називають елементами матриці. Положення елементів строго фіксовано: у кожній клітці повинний розташовуватися тільки один елемент і жодна клітка не повинна залишатися вільної. У загальному позначенні елемента 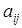перший індекс i завжди вказує номер рядка, а другий — номер стовпця. Елемент, розташований у ij-клітці, називають ij-елементом.

Матриця позначається однією буквою (часто букви, що позначають матриці, набирають жирним шрифтом чи постачають якими-небудь додатковими символами). Однак незалежно від прийнятого способу позначення матриця завжди є сукупністю таблично упорядкованих елементів. Дві матриці рівні, якщо і тільки якщо рівні їхній відповідні елементи, тобто A=В за умови a_ij=b_ij (i = 1,2, ... , т; j = 1,2, ... , n). Ясно, що порівнювати можна тільки матриці однакового розміру, між елементами яких визначене відношення рівності.

Матриці, елементами яких є речовинні чи комплексні числа, називають відповідно речовинними чи комплексними. Нехай А — комплексна 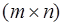- матриця з елементами a_ij=a_ij+ib_ij. Матриця 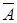того ж розміру з елементами a*_ij=a_ij-ib_ij називається комплексно - сполученою з А.

Часто для спрощення нульові елементи в таблицю не записують, але при цьому мають на увазі, що порожні клітки також містять числа (нулі).

Крім приведеної вище клітинного запису, використовують і інші способи представлення матриць, наприклад:

; ; .

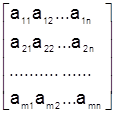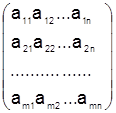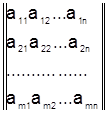Матриці вперше з'явилися в середині минулого сторіччя в роботах англійських математиків А. Кэли й У. Гамільтона. Представлення сукупностей елементів у виді матриць і розроблені правила операцій над ними виявилися дуже плідними в математиці і знайшли широке застосування у фізиці, техніці, економіці. Істотний внесок у розробку загальної теорії матриць і її додатків внесли радянські математики И. А. Лаппо-Данілевський. А. Н. Крилов, Ф. Р. Гантмахер, М. Г. Крейн.