Примеры. 34. Пользуясь формулой Остроградского-Гаусса, вычислить интеграл , где Ф – внешняя сторона сферы (x–a)2+(y-b)2+(z–c)2=R2

34. Пользуясь формулой Остроградского-Гаусса, вычислить интеграл 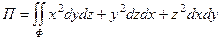, где Ф – внешняя сторона сферы (x–a)²+(y-b)²+(z–c)²=R².

Решение. По формуле Остроградского-Гаусса имеем:

,

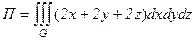где G – шар (x–a)²+(y-b)²+(z–c)²£R². Для вычисления интеграла перейдем к сферическим координатам:

x=a+rcosjsinq, y=b+rsinjsinq, z=c+rcosq, 0 £ j £ 2p, 0 £ q £ p.

Якобиан перехода равен r²sinq. Уравнение границы области G имеет вид r = R. Следовательно, .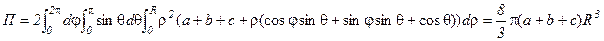

Ответ: .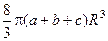

Пусть задана ориентированная поверхность (Ф), т.е. такая поверхность, в каждой точке которой выбран единичный вектор 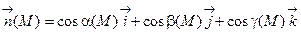, меняющийся на поверхности непрерывно. В случае замкнутой поверхности в качестве 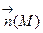будем всегда выбирать вектор внешней нормали.

Потоком П векторного поля 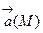через ориентированную поверхность (Ф) называют поверхностный интеграл (первого рода): .

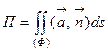Дивергенция (расходимость) векторного поля 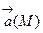может быть определена выражением: 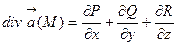, т.е. дивергенция векторного поля 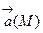представляет собой скалярное поле в области G.

Если 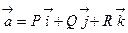– разложение векторного поля 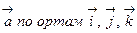, то формулу, определяющую поток, можно записать в виде:

,

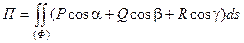либо записать в форме поверхностного интеграла (второго рода):

.

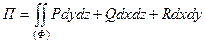Теперь теорему Остроградского-Гаусса можно сформулировать следующим образом: поток векторного поля через замкнутую поверхность равен тройному интегралу от дивергенции векторного поля по объему, ограниченному этой поверхностью.

35. Найти поток векторного поля 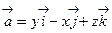через замкнутую поверхность (Ф), состоящую из поверхности конуса x²+y²=z² и плоскости z=1. См. рис 3.

Решение. Имеем .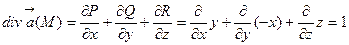

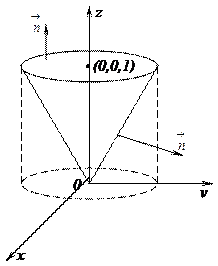Следовательно, 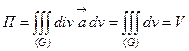, где V–объем конуса.

Так как 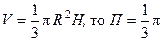. Ответ: p/3.

36. Найти поток векторного поля 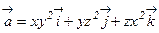через поверхность сферы x²+y²+z²=R².

Решение. В данном случае поверхность (Ф) – замкнутая, поэтому для вычисления потока можно применить формулу Гаусса - Остроградского. Имеем

.

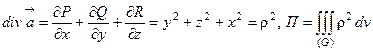Рис. 3.

Вычисляем интеграл в сферических координатах:

.

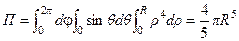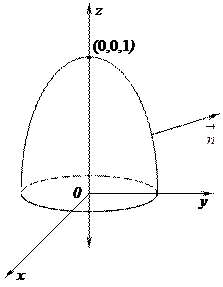
37. Найти поток векторного поля 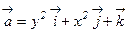через часть поверхности параболоида 1 – z = x²+y² (0 £ z £ 1). См. рис. 4.

Решение. Обозначим данную поверхность через (Ф₁) и рассмотрим замкнутую поверхность 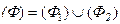, где (Ф₂) – круг радиуса R=1 на плоскости XOY. Из формулы Гаусса - Остроградского вытекает, что поток через поверхность (Ф) равен нулю. Действительно, для данного поля

.

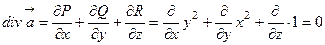Рис. 4

Следовательно, 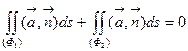. Отсюда искомый поток через поверхность (Ф₁):

.

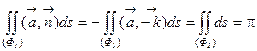Ответ: p.

38. Пользуясь формулой Остроградского-Гаусса, вычислить поток векторного поля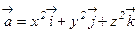

через полную поверхность конуса .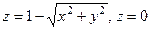

Решение. Найдем дивергенцию векторного поля: 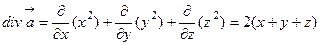. Тогда .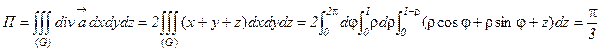