Линейная модель множественной регрессии с гетероскедастичными остатками

Нарушение условий о случайном характере ошибок и равенстве дисперсий ошибок для разных наблюдений – Е(εiεj)=0 при i≠j приводит к тому , что оценки, полученные с помощью МНК оказываются смещенными и неэффективными. Для проверки случайного характера остатков строиться график зависимости остатков ei от теоретических значений результативного признака:

Если на графике получена горизонтальная полоса, то остатки ei представляют собой случайные величины и МНК оправдан, те­оретические значения ух хорошо аппроксимируют фактические значения у.

В остальных случаях необходимо либо применять дру­гую функцию, либо вводить дополнительную информацию.

Гомоскедастичность остатков означает, что дисперсия остатков ei одинакова для каждого значения х. Если это условие не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции. а — дисперсия остатков растет по мере увеличения х; б — дисперсия остатков достигает максимальной величины при средних значениях переменной х и уменьшается при минимальных и максимальных значениях х; в — максимальная дисперсия остатков при малых значениях х и дисперсия остатков однородна по мере увеличения значений х.

При появлении гетероскедостичности остатков нарушается третья предпосылка МНК, что приводит смещенности оценок параметров регрессии, а также уменьшению их эффективности. Становится затруднительным использовать формулы для стандартного отклонения этих параметров, завышается t-статистика, что дает неправильное представление о точности регрессии.

При нарушении гомоскедастичности имеем

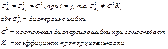к_i- может меняться при переходе от одного фактора к другому.

18. Мультиколлинеарность и методы ее устранения.На практике часто возникает ситуации, когда построенная регрессия является неудовлетворенной, т.е. t-статистики большинства оцененных параметров малы, что свидетельствует о незначимости соответствующих независимых переменных. В то же время F-статистика может быть достаточно большой, что говорит о значимости регрессии в целом. Одна из возможных причин такого явления – мультиколлинеарность, которая возникает при наличии высокой корреляции между независимыми переменными. Строгая (полная) мультиколлинеарность возникает редко. Чаще встречается частичная. Она может возникнуть в силу разных причин. Например, несколько независимых переменных могут иметь общий временной тренд, в частности значение одной независимой переменной является лагированными значениями другой.

Наиболее характерные признаки мультиколлинеарности:

1)среди парных коэффициентов корреляции между независимыми переменными имеются значения 0,75-0,8 и выше.

2)небольшое изменение исходных данных (например добавление новых наблюдений) приводит к существенному изменению оценок параметров модели.

3)оценки параметров имеют большие стандартные ошибки, малую значимость, в то же время модель целиком является значимой (высокое значение R² и F-статистики).

4)оценки параметров имеют неправильные с точки зрения содержательной интерпретации знаки или чрезмерно большие значения.

Методы устранения мультиколлинеарности:

1. удаление из регрессионной модели лишних факторов. Однако это делают аккуратно потому что исключение лишних факторов может привести к искажению содержательного смысла модели и смещению МНК оценок.

2. Преобразование факторов при котором уменьшается корреляция между ними. Например переход от первоначальных значений фактора к первым разностям: Δ₁=x_i+1-x_i/

3. использование в модели регрессии взаимодействия факторов, например, в виде их произведений.

4. использование метода главных компонент. Суть этого метода заключается в сокращении числа независимых факторов до наиболее существенно влияющих. Это достигается путем линейного преобразования всех объясняющих факторов в новые переменные – главные компоненты. При этом требуется чтобы первой главной компоненте соответствовал максимум общей дисперсии всех объясняющих переменных; второй компоненте – максимум оставшейся дисперсии после того, когда влияние первой главной компоненты исключается и т.д.