Випадок неоднорідного рівняння

Якщо в однорідному ізотропному нескінченому стержні діють джерела тепла інтенсивності 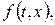то температура 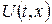повинна бути розв’язком неоднорідного рівняння теплопровідності

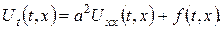(23)

Розв’язок задачі Коші (23), (21), якщо функці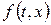ї і 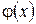є неперервними і обмеженими відповідно в Ω та на осі 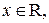шукається у вигляді суми 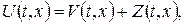де функці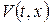ї і 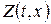– розв’язки наступних задач Коші:

1) 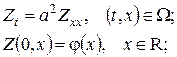2)

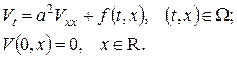
Розв’язок першої задачі дається формулою Пуассона (22):

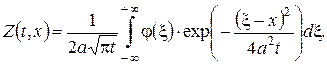
Згідно принципу Дюгамеля функцію 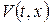шукаємо у вигляді інтеґрала: 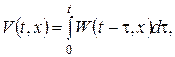де 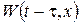визначається із задачі Коші

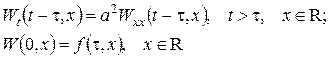
і дається формулою Пуассона

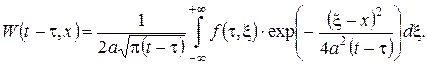
Тоді розв’язок задачі Коші (23), (21) буде мати вигляд

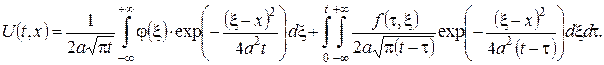(24)

4. Змішані задачі для напівнескінченого стержня з теплоізольованою бічною поверхнею

При дослідженні процесів поширення тепла в напівнескінченому стержні з теплоізольованою бічною поверхнею, кінець якого розміщений у початку координат, ми приходимо до однієї з наступних змішаних задач:

в області 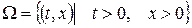знайти розв’язок рівняння

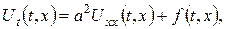(25)

який справджує початкову умову

- 19 -

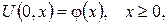(26)

та одну з крайових умов на кінці стержня:

1) 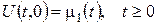(задана температура); (27)

2) 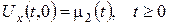(заданий тепловий потік); (28)

3) 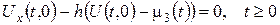(заданий теплообмін по закону Ньютона з навколишнім середовищем, температура якого рівна μ₃(t)).

Універсальним методом інтеґрування змішаних задач такого вигляду є метод інтеґрального перетворення Фур’є (див. [6], стор. 263-265, а також 312-316). Проте в деяких частинних випадках вдається знайти розв’язок за допомогою простіших методів (при цьому функці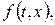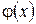ї і 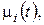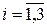вважаємо обмеженими і неперервними відповідно в областях Ω, 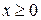та 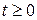). Зокрема, це стосується випадків, коли кінець стержня теплоізольований (μ₂(t)≡0) або підтримується при нульовій температурі (μ₁(t)≡0).

1) Метод непарного продовження. Змішана задача

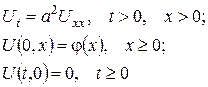
(кінець стержня підтримується при нульовій температурі) при 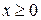еквівалентна задачі Коші

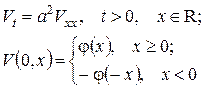
(задаємо непарне продовження початкової функції). Тоді розв’язок змішаної задачі 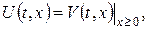де 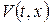знаходиться за допомогою формули Пуассона (22).

2) Метод парного продовження. Змішана задача

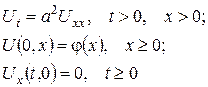
(кінець стержня теплоізольований) при 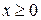еквівалентна задачі Коші

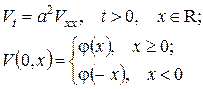
(задаємо парне продовження початкової функції). Тоді знову розв’язок змішаної задачі 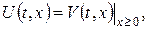де 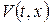знаходиться за допомогою формули Пуассона (22).

- 20 -

Зауваження 1. Якщо у змішаній задачі (25), (26), (27) μ₁(t)≡0 (або у змішаній задачі (25), (26), (28) μ₂(t)≡0), то розв’язок можна знайти, застосувавши принцип Дюгамеля аналоґічно до задач Коші. Інший спосіб – задати парне (непарне) продовження не тільки початкової функції, а й інтенсивності джерел тепла: тоді розв’язок еквівалентної задачі Коші знаходиться за допомогою формули (24).

Зауваження 2. Якщо у змішаній задачі для напівнескінченого стержня крайова умова неоднорідна, то її завжди можна звести до однорідної, підібравши деяку обмежену допоміжну функцію, котра справджує цю крайову умову. Зокрема, підстановкою 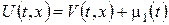зодноріднюється крайова умова (27), а підстановкою 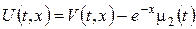– крайова умова (28).

ПРИКЛАД.Знайти розподіл температури в однорідному ізотропному напівнескінченому стержні з теплоізольованою бічною поверхнею, кінець якого підтримується при нульовій температурі, якщо початкова температура стержня рівна 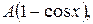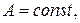а всередині стержня діють джерела тепла інтенсивності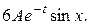

Розв’язання. Математична модель задачі:

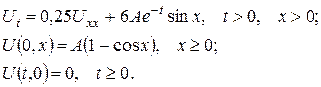
Розв’язок шукаємо у вигляді суми 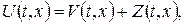де

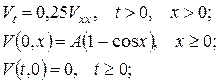1) 2)

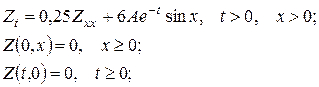
До першої змішаної задачі застосуємо метод непарного продовження: 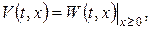де

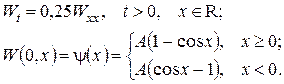
Згідно формули Пуассона (22)

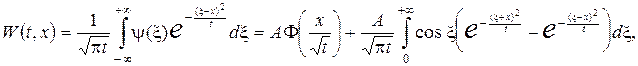
де 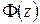– “інтеґрал помилок”.

- 21 -

Згідно принципу Дюгамеля розв’язок другої змішаної задачі будемо шукати у вигляді інтеґрала 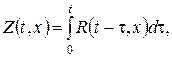де

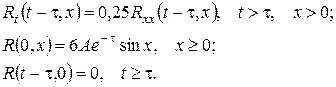
Початкова функція є непарною, тому можна одразу застосувати формулу (22). Одержимо:

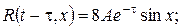
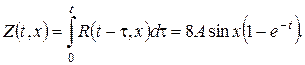
Тоді розв’язок вихідної змішаної задачі буде (для всіх )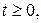

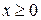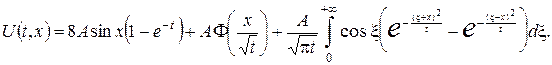
КОНТРОЛЬНІ ПИТАННЯ

1.Які фізичні процеси приводять до змішаних задач для рівнянь параболічного типу?

2.Запишіть рівняння теплопровідності, якщо

а) бічна поверхня стержня теплоізольована, а всередині його діють джерела тепла інтенсивності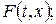

б) через бічну поверхню стержня проходить вільний теплообмін із навколишнім середовищем, температура якого рівна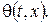

3.Запишіть крайові умови, якщо

а) кінці стержня підтримуються при нульовій температурі;

б) кінці стержня теплоізольовані;

в) на лівому кінці підтримується температура 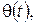а до правого підводиться тепловий потік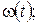

г) на кінцях стержня проходить теплообмін із навколишнім середовищем, температура якого рівна нулеві.

4.У чому полягає основна ідея методу відокремлення змінних?

5.Як будується розв’язок змішаної задачі для однорідного ізотропного стержня при наявності внутрішніх джерел тепла?

6.Наведіть метод побудови розв’язку змішаної задачі для рівняння теплопровідності у випадку

а) загальної змішаної задачі;

- 22 -

б) задачі зі стаціонарними неоднорідностями.

7.Як ставиться задача Коші для одновимірного рівняння теплопровідності?

8.При яких умовах формула Пуассона дає розв’язок задачі Коші для одновимірного рівняння теплопровідності?

9.Як будується розв’язок задачі Коші у випадку неоднорідного рівняння теплопровідності?

10.Наведіть методи побудови розв’язку змішаної задачі для напівнескінченого стержня, якщо

а) кінець стержня підтримується при нульовій температурі;

б) кінець стержня теплоізольований.

11.Наведіть фізичну інтерпретацію фундаментального розв’язку однорідного рівняння теплопровідності та формули Пуассона.

12.Сформулюйте принцип максимуму для розв’язків рівняння теплопровідності.

13.Сформулюйте теореми про єдиність розв’язку змішаних задач для рівняння теплопровідності та його неперервну залежність від початкової та крайових умов.

14.Сформулюйте теореми про єдиність розв’язку задачі Коші для рівняння теплопровідності та його неперервну залежність від початкової функції та інтенсивності внутрішніх джерел тепла.

15.Запишіть крайову умову, яку справджує інтеґрал Пуассона (22), якщо початкова функція є:

а) непарною;

б) парною.