Экспоненциальный закон распределения

Экспоненциальное (показательное) распределение -это распределение вероятностей, которое описывается дифференциальной функцией.

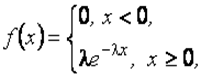
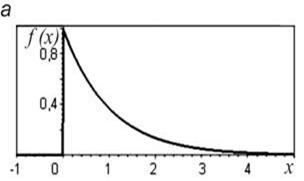
Экспоненциальное распределение определяется одним параметром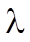

Вопрос 6 Функция распределения. Плотность вероятности. Стандартные интервалы.

Функция распределения = интегральная функция распределения – это вероятность того, что случайная величина Х примет значение меньше некоторого наперед заданного числа х- малое:

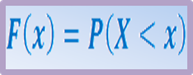
Свойства:

1)

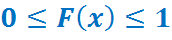
2)

Для дискретных случайных величин а)

Для непрерывных случайных величин б)

а) 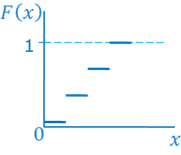б)

Плотность распределения вероятностей, илиплотность распределения непрерывнойслучайной величины Х=дифференциальная функция распределения-производная ее функции распределения.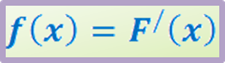

Свойства плотности вероятности:

1. Неотрицательная функция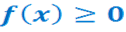

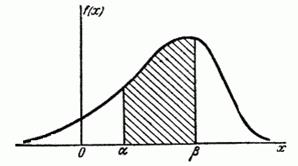
2. Площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

3. Вероятность попадания непрерывной случайной величины в интервал [а,b] равна определенному интегралу от ее плотности вероятности в пределах от a до b.

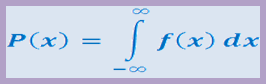
Стандартные интервалы???

Вопрос 7.Генеральная совокупность и выборка. Объем выборки. Репрезентативность.

Генеральная совокупность - это множество всех мыслимых значений наблюдений, однородных относительно некоторого признака, которые могли быть сделаны.

Объем генеральной совокупности N.

Выборка– совокупность случайно отобранных наблюдений для непосредственного изучения из генеральной совокупности.

Выборка характеризуется:

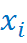– варианта- каждый элемент выборки.

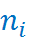- частота встречаемости- число наблюдений варианты.

Объем выборки - это количественная характеристика выборки. Это количество вариант в выборке. Это число случаев, включенных в выборочную совокупность.

Репрезентативность (фр. Representative - представляющий) - это соответствие характеристик выборки характеристикам генеральной совокупности.

Репрезентативность- это свойство выборки представлять параметры генеральной совокупности.

Вопрос 8Статистическое распределение (вариационный ряд) Гистограмма.

Статистическое распределение - это совокупность вариант 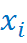и соответствующих им частот .

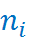Вариационный ряд - последовательность вариант, записанных в возрастающем порядке.

Гистограмма - это ступенчатая фигура, состоящая из смежных прямоугольников, построенных на одной прямой, основания которых одинаковы и равны ширине класса, а высота равна или частоте попадания в интервал 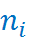или относительной частоте 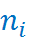/n

Ширину интервала I можно определить по Формуле Стерджеса:

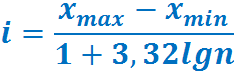
Вопрос 9.Характеристики положения (мода, медиана, выборочная средняя) и рассеяния (выборочная дисперсия и выборочное среднее квадратическое отклонение).

Мода (Мо)– наиболее часто встречающаяся варианта в данной совокупности.

Мода (Мо)- это такое значение варианты, что предшествующие и следующие за ней значения имеют меньшие частоты встречаемости.

Медиана (Ме)- это значение признака, относительно которого вариационный ряд делится на две равные части.

Выборочная средняя – это среднее арифметическое значение вариант статистического ряда:

Характеристики рассеяния определяют отклонение каждой варианты от средней арифметической.

Выборочная дисперсия – это среднее арифметическое квадратов отклонения вариант от их среднего значения:

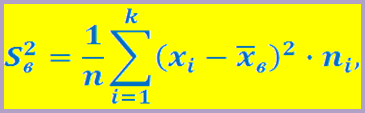
Среднее квадратическое отклонение– стандартное отклонение- квадратный корень из выборочной дисперсии:

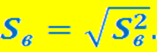
n – объем выборки

ni – частота встречаемости

xi – варианта

х – выборочное среднее

Вопрос 10Оценка параметров генеральной совокупности по характеристикам ее выборки (точечная и интервальная)

Оценка параметра - это любая функция от значений выборки.

Параметры выборки:

1) Выборочное среднее

2) Выборочная дисперсия

Параметры генеральной совокупности:

1) Генеральное среднее

2) Генеральная дисперсия

Точечная оценка - это выборочная характеристика, используемая в качестве приближенного значения неизвестной генеральной характеристики.

- Определяется одним числом (точкой на числовой оси)

- Выборка должна быть большого объема.

- Дает лишь некоторое приближенное значение параметра.

Требование: несмещенная, состоятельная, эффективная.

Точечную оценку называют несмещенной, если ее математическое ожидание равно оценивающему параметру при любом объеме выборки.

1) Генеральное среднее равно математическому ожиданию выборочной средней. 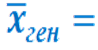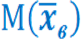Следовательно:

Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя:

2) Генеральная дисперсия не равна математическому ожиданию выборочной дисперсии.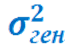

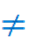
Следовательно: выборочная дисперсия- это смещенная оценка

генеральной дисперсии.

Тут можно сказать об исправленной дисперсии. (а можно и не сказать)

Исправленная дисперсия (более точная)

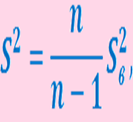
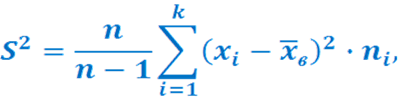
Генеральная дисперсия равна математическому ожиданию исправленной дисперсии.

Интервальная оценка - это числовой интервал, содержащий неизвестный параметр генеральной совокупности заданной вероятностью.

- Определяется двумя числами – границами интервала.

- Более точная, надежная и информативная, так как дает информацию о степени близости соответствующему теоретическому параметру.

- Используется, если выборка малого объема.

Вопрос 11.Доверительный интервал и доверительная вероятность.

Доверительный интервал — это интервал, в котором с той или иной заранее заданной вероятностью находится генеральный параметр.

,

(Р≥0,95)

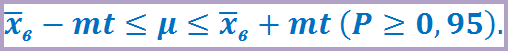где 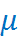- генеральное среднее; 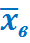- выборочное среднее;

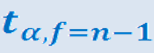-нормированный показатель распределения Стьюдента, с (n-1) степенями свободы, который определяется вероятностью попадания генерального параметра в данный интервал; х- средняя ошибка выборочной средней.

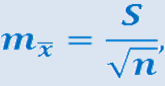
Доверительная вероятность P это такая вероятность, что событие 1-Р можно считать невозможным.

Признана достаточной для уверенного суждения о генеральных параметрах на основании известных выборочных показателей.

Обычно в качестве доверительных используют вероятности, близкие к 1. Тогда событие, что генеральный параметр попадет в этот интервал будет практически достоверным.

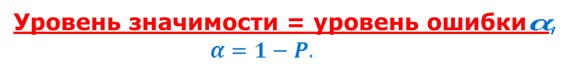
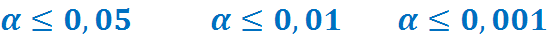Вопрос 12сравнение средних значений двух нормально распределенных генеральных совокупностей.

Схема проверки гипотезы:

1) Выдвигаем нулевую гипотезу H0. Это основная гипотеза.

Сущность H0: разница между сравниваемыми генеральными параметрами = 0, и различия, наблюдаемые между выборочными данными носят случайный характер.

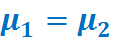или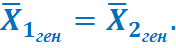

2) Формулируем альтернативную гипотезу Н1 конкурирующую с Н0. Это логическое отрицание Н0.

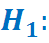
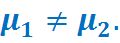
3) Задаем уровень значимости критерия.

Уровень значимости критерия а - это вероятность ошибки отвергнуть Н0, если на самом деле она верна.

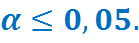
4) Для проверки нулевой гипотезы можно использовать параметрический критерий Стьюдента сравнения средних.

Величину критерия находим по формуле:

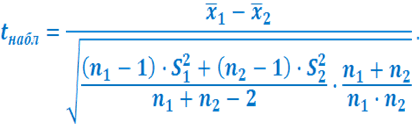
Обычно расчет ведется на ЭВМ.

Это отношение имеет t-распределение Стьюдента с степенями свободы.

5) По таблице известного распределения находим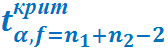

6) Сравниваем

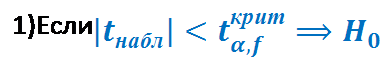
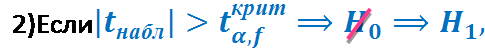
7) Выводы

1)Различие недостоверно.

2)Различие достоверно, значимо