Типовых задач линейного программирования

1) Задача распределения ресурсов

Пусть на некотором предприятии для изготовления n видов продукции Р₁, Р₂, …, Р_n используют m видов сырья (ресурсов) S₁, S₂, …, S_m. Объём (запас) каждого вида сырья ограничен и известен: b₁, b₂, …, b_m. Для изготовления единицы j-го вида продукции требуется а_ij (i = 1, 2, …, m; j = 1, 2, …, n) единиц каждого i-го вида сырья. Известна прибыль, получаемая от реализации единицы каждого вида продукции: с₁, с₂, …, с_n. Сколько единиц продукции каждого вида нужно произвести, чтобы уложиться в имеющиеся запасы сырья (ресурсов) и получить максимальную прибыль?

Для наглядности представим условия задачи в виде таблицы:

Вид	Запас			аij
сырья	сырья	Р1	Р2	…	Рn
S1 S2 … Sm	b1 b2 … bm	а11 а21 …. аm1	а12 а22 …. аm2	… … … …	а1n а2n …. аmn
Прибыль		с1	с2	…	сn

Составим математическую модель (ММ) данной ЗЛП, т.е. опишем неизвестные, целевую функцию, систему ограничений и условия неотрицательности.

Неизвестные. По условию задачи неизвестно, сколько единиц продукции каждого вида нужно произвести. Всего на данном предприятии изготавливают n видов продукции. Обозначим через х_j – количество единиц продукции j-го вида (j = 1, 2, …, n). Таким образом, 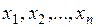- неизвестные данной ЗЛП.

Целевая функция. В данной задаче требуется получить максимальную прибыль от реализации продукции. Следовательно, в качестве целевой функции будет выступать прибыль.

Если единица продукции первого вида приносит прибыль с₁, то прибыль от реализации х₁ единиц продукции составит с₁х₁. Аналогично, х₂ единиц продукции второго вида дадут прибыль с₁х₁, и т.д.

Общую прибыль, получаемую от реализации всей продукции, можно представить в виде 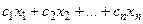. Поскольку эту функцию нужно максимизировать, то получим F (Х) = 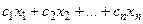→ max.

Система ограничений. Сначала найдём, сколько сырья первого вида необходимо для производства всей продукции.

Если на единицу продукции 1-го вида уходит а₁₁ единиц сырья первого вида, то на х₁ единиц продукции 1-го вида уйдёт а₁₁х₁ сырья первого вида. Для выпуска х₂ единиц продукции 2-го вида потребуется а₁₂х₂ единиц сырья первого вида и т.д. Чтобы произвести х_n единиц продукции n-го вида потребуется а_1nх_n единиц сырья первого вида. Всего потребуется 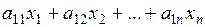единиц сырья первого вида.

Так как b₁ - количество сырья первого вида и, чтобы его расход не превышал имеющегося запаса, должно выполняться неравенство .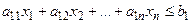

Аналогично составляются ограничения для ресурсов второго вида:

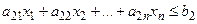и т.д.

Система ограничений для данной задачи примет вид:

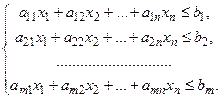
Условия неотрицательности переменных: 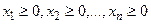, т.к. нельзя выпускать отрицательное число единиц продукции.

Таким образом, ММ задачи использования ресурсов имеет вид:

F(Х) = 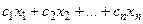→ max,

.

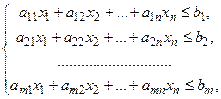
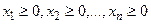2) Задача о рационе питания

В общем виде эту задачу можно сформулировать следующим образом: требуется составить ежедневный рацион питания человека исходя из имеющихся в наличии продуктов так, чтобы общая стоимость использованных продуктов была минимальной. При этом человек должен получать не менее определённого количества питательных веществ, таких, как витамины, белки, жиры, углеводы, минералы и т.п. Каждый продукт содержит разную комбинацию этих веществ. Известна цена единицы веса каждого продукта.

Конкретизируем условия ЗЛП. Пусть имеется n видов продуктов Р₁, Р₂, …, Р_n и перечень из m необходимых питательных веществ S₁, S₂, …, S_m. Пусть а_ij (i = 1, 2, …, m; j = 1, 2, …, n) - содержание (в весовых единицах) i-го питательного вещества в единице веса j-го продукта; b_i - минимальная суточная потребность человека в i-м питательном веществе. Известна цена единицы веса каждого продукта: с₁, с₂, …, с_n.

Сколько единиц веса продуктов каждого вида нужно взять для ежедневного рациона питания человека, чтобы уложиться в имеющиеся запасы продуктов, получить не менее заданного количества питательных веществ и заплатить наименьшую сумму денег?

Представим условия задачи в виде таблицы.

Питательное	Суточная			аij
вещество	потребность	Р1	Р2	…	Рn
S1 S2 … Sm	b1 b2 … bm	а11 а21 …. аm1	а12 а22 …. аm2	… … … …	а1n а2n …. аmn
Стоимость веса	единицы продукта	с1	с2	…	сn

Составим ММ данной ЗЛП.

Неизвестные. По условию задачи неизвестно, сколько единиц веса

продуктов каждого вида нужно включить в рацион питания. Всего имеется n видов продуктов. Обозначим через х_j – количество единиц продуктов j-го вида (j = 1, 2, …, n). Таким образом, 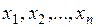- неизвестные данной ЗЛП.

Целевая функция. В данной задаче требуется так составить рацион питания, чтобы общие затраты на продукты были минимальными. Следовательно, в качестве целевой функции будет выступать общая стоимость использованных в рационе продуктов.

Если единица веса первого вида продукта питания стоит с₁, то цена х₁ единиц веса продуктов первого вида составит с₁х₁. Аналогично, х₂ единиц веса продуктов второго вида будут стоить с₁х₁, и т.д.

Общую стоимость составленного рациона питания можно представить в виде 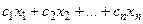. Поскольку эту функцию нужно минимизировать, то получим

F(Х) = 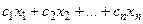→ min.

Система ограничений. Сначала найдём, сколько продуктов первого вида необходимо включить в рацион питания.

Если в единице веса продукта первого вида содержится а₁₁ единиц веса питательного вещества первого вида, то в х₁ единиц веса продуктов первого вида будет а₁₁х₁ единиц веса питательного вещества первого вида. В х₂ единицах веса продуктов второго вида содержится а₁₂х₂ единиц веса питательного вещества первого вида и т.д. В х_n единицах веса продуктов n-го вида будет содержаться а_1nх_n единиц веса питательного вещества первого вида. Всего потребуется 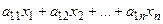единиц веса питательного вещества первого вида.

Так как b₁ – минимальная суточная потребность человека в первом питательном веществе, то должно выполняться неравенство

.

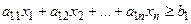Аналогично составляются ограничения для второго вида питательного вещества: 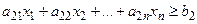и т.д.

Система ограничений для данной задачи примет вид:

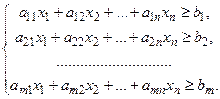
Условия неотрицательности: 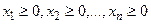, т.к. не может быть отрицательного количества продуктов.

Таким образом, ММ задачи о рационе питания имеет вид:

F(Х) = 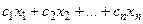→ min,

.
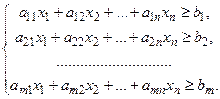
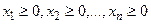