Порядок виконання завдання

1. Виписати для заданого варіанту числові дані. В певному масштабі накреслити схему заданої системи з зазначенням її лінійних розмірів і зовнішніх навантажень.

2. Встановити ступінь статичної невизначуваності системи.

3. Розглянути можливі варіанти основної системи і вибрати з них раціональний для проведення подальших розрахунків.

4. Зобразити еквівалентну схему.

5. Скласти систему канонічних рівнянь методу сил для даного варіанту основної системи.

6. Побудувати для вибраної основної системи епюри моментів від заданих навантажень та одиничних сил.

7. Обчислити коефіцієнти канонічних рівнянь методу сил.

8. Вирішити систему канонічних рівнянь і визначити невідомі зусилля .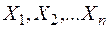

9. Побудувати остаточні епюри моментів для заданої статично невизначуваноїсистеми.

10. Аналізуючи епюри внутрішніх силових факторів, визначити небезпечний переріз і відзначити його на епюрах та розрахунковій схемі.

11. Зобразити профіль небезпечного перерізу, вказавши величини і напрямки дії внутрішніх згинальних та крутних моментів.

12. Побудувати епюри напружень в небезпечному перерізі, визначити найбільш напружені точки перерізу і відзначити їхнє положення на профілі поперечного перерізу.

13. Зобразити напружений стан в означених точках перерізу на нескінченно малому координатному елементі. Встановити тип напруженого стану.

14. Записати умову міцності, використовуючи енергетичну теорію граничного напруженого стану, і визначити розміри поперечного перерізу заданої конструкції.

РПЗ складається з трьох обов’язкових для рішення задач:

1. Розкрити статичну невизначуваність багатопрольотної нерозрізної балки (додаток 1). Чисельні дані наведені в таблиці Д.1.

2. Розкрити статичну невизначуваність плоскої рами (додаток 2).Чисельні дані наведені в таблиці Д.2.

3. Для просторової рами (додаток 3) розкрити статичну невизначуваність і із умови міцності при сумісній дії згинання та кручення визначити розміри тонкостінного поперечного перерізу. Чисельні дані наведені в таблиці Д.3. Всі необхідні для розрахунку дані – форма і співвідношення розмірів поперечного перерізу наведено в додатку 4.

В додатках 5 і 6 наведені схеми і чисельні дані для контрольних задач підвищеної складності.

Рішення поставлених комплексних задач можна умовно поділити на два етапи. На першому етапі необхідно розкрити статичну невизначуваність запропонованого варіанту вхідної системи, використовуючи метод сил. Завершенням першого етапу розрахунку є побудова епюр згинальних та крутних моментів, поздовжніх та поперечних сил для вхідної системи.

При спільній дії згинального і крутного моментів в поперечних перерізах замкнутого тонкостінного профілю виникають нормальні і дотичні напруження.

Осьові моменти інерції, що визначають згинальну жорсткість тонкостінного замкнутого профілю рами, що має дві і більш осей симетрії, обчислюються наступним чином:

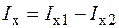(3.1)

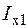Тут і 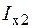– осьові моменти інерції простих перерізів (прямокутник, коло), що складають поперечний переріз.

Момент інерції кручення для замкнутих тонкостінних перерізів визначається по формулі [2]:

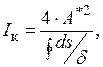(3.2)

де 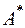– площа, обмежена середньою лінією контуру перерізу;

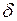– товщина поперечного перерізу.

Як і для суцільного брусу, величина нормальних напружень обчислюється по формулі:

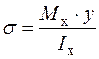(3.3)

Максимальні значення нормальних напружень мають місце при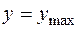

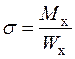(3.4)

Дотичні напруження в перерізі замкнутого тонкостінного профілю від дії крутного моменту обчислюються по формулі Бредта:

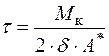(3.5)

Внаслідок малості величини 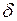приймається рівномірний закон розподілу дотичних напружень по товщині перерізу, так що для перерізів змінної товщини справедлива рівність

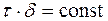(3.6)

Напрямок дотичних напружень в будь-якому поперечному перерізі системи співпадає з напрямком крутного моменту. Для кільцевих перерізів, по аналогії з крученням товстостінних профілів, виконується умова ортогональності дотичних напружень до радіус-вектору довільної точки перерізу, проведеному з центру кручення.

Записуючи еквівалентні напруження по енергетичній теорії граничного стану як функцію геометричних характеристик плоского перерізу, з умови міцності визначаються поперечні розміри перерізу вхідної конструкції.

Додаток 1.

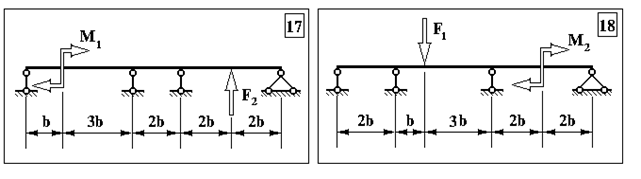
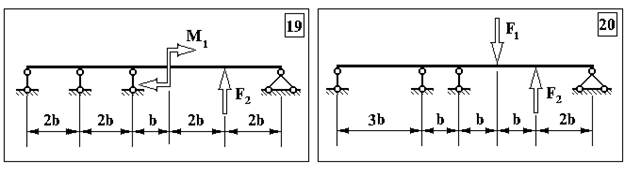
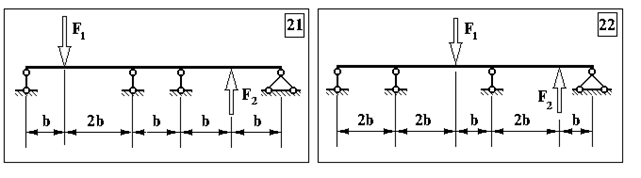
Задача 1. Визначення внутрішніх зусиль у статично невизначуваних балках

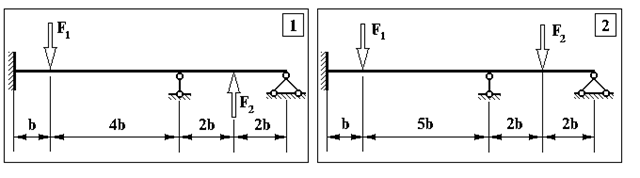
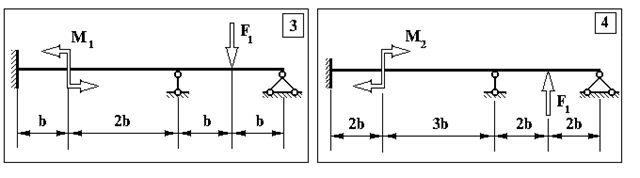
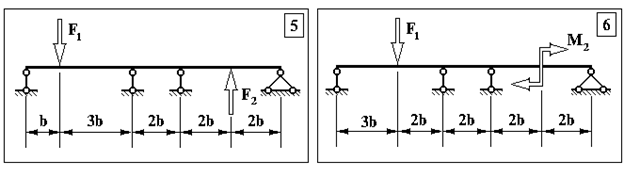
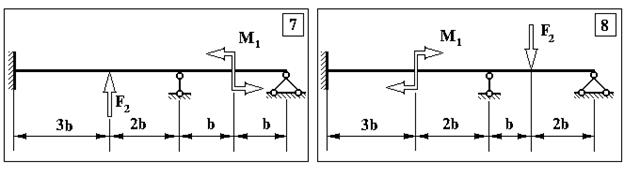
Продовження додатку 1.

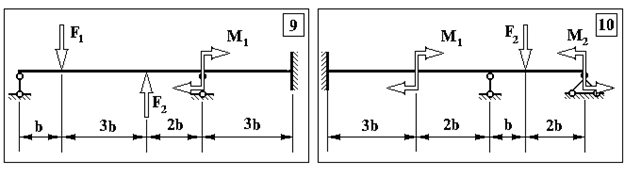
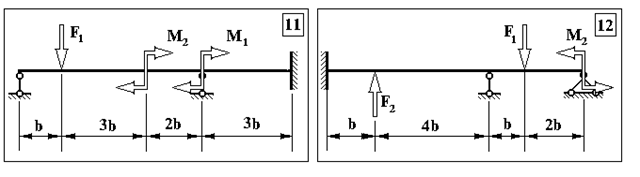
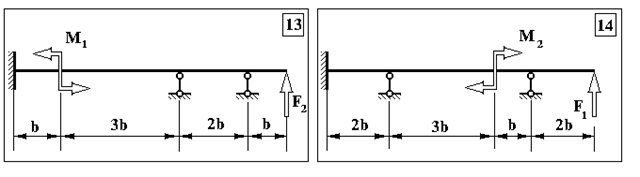
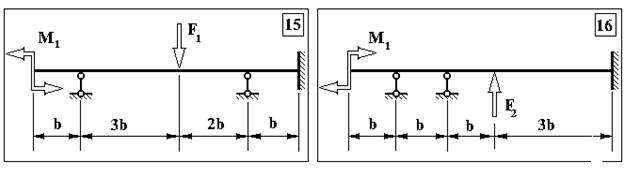
Продовження додатку 1.

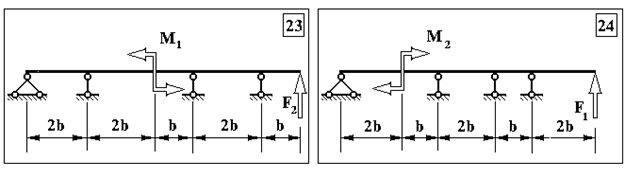
Таблиця Д.1.

Чисельні дані до задачі №1.

№ п/п	F1, кН	F2 , кН	M1 , кНм	M2, кНм	b, м
					0,7
				-4	0,6
					0,8
					0,5
					0,6
					0,4
		-6			0,8
				-7	0,7
		-20			0,6
		-7			0,5
					0,4
				-9	0,3
			-6		0,7
			-8		0,8
	-7				0,5
					0,6
					0,7
				-9	0,4
					0,3
					0,8
		-9			0,6
	-15				0,7
				-4	0,4
				-5	0,5

Додаток 2.

Задача 2. Визначення внутрішніх зусиль у статично невизначуваних рамах

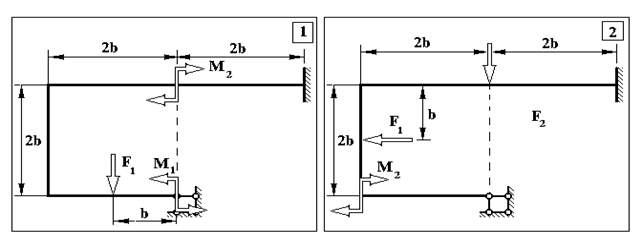
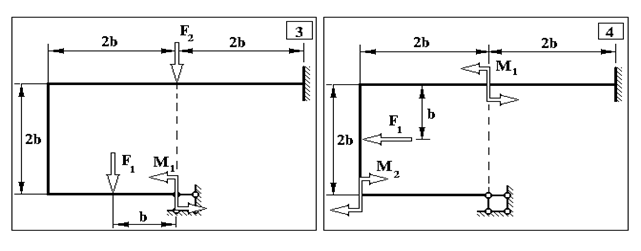
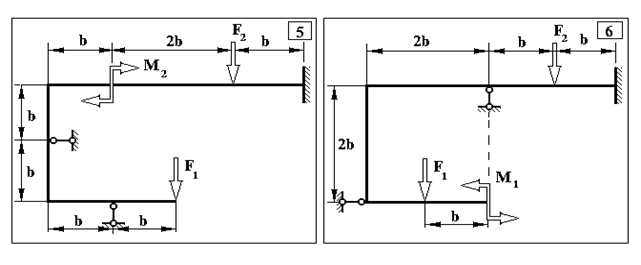
Продовження додатку 2.

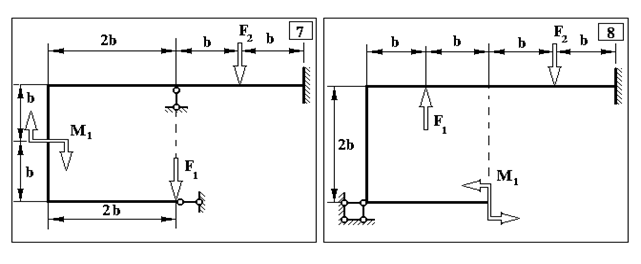
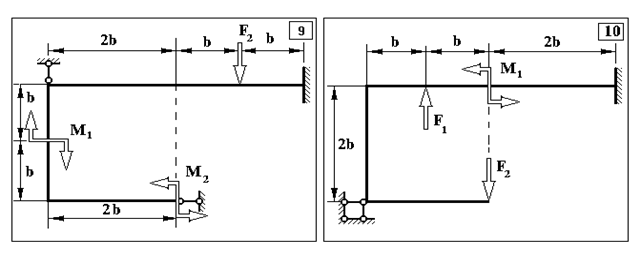
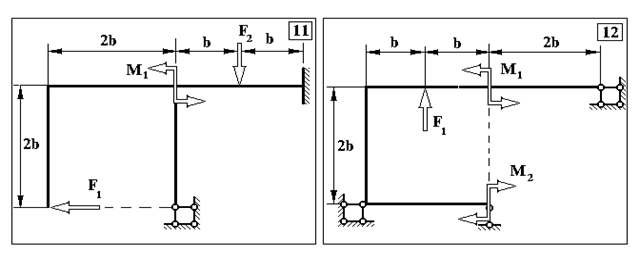
Продовження додатку 2.

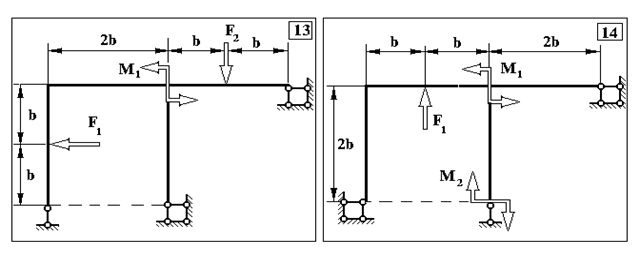
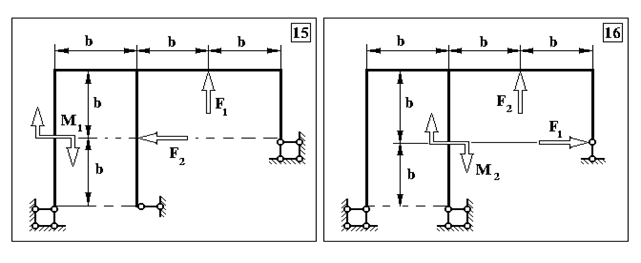
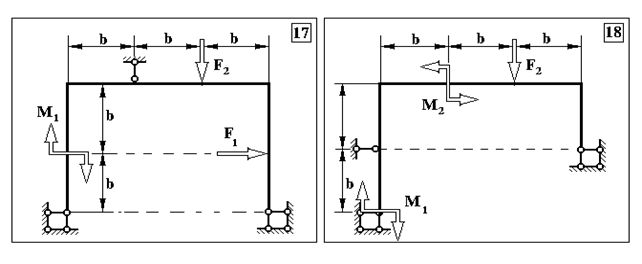
Продовження додатку 2.

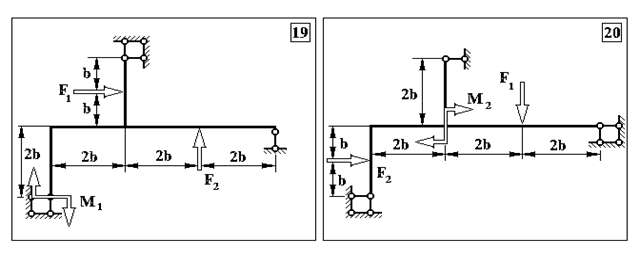
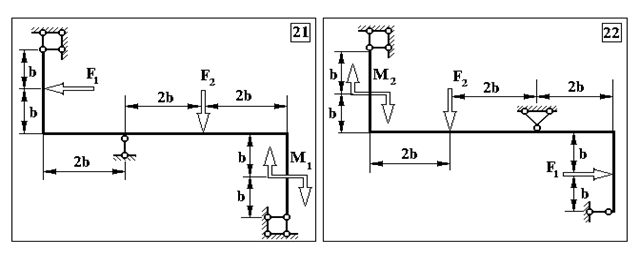
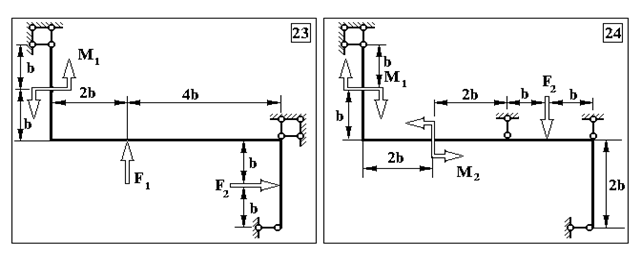
Таблиця Д.2.

Чисельні дані до задачі №2

№ п/п	F1, кН	F2 , кН	M1 , кНм	M2, кНм	b, м
					0,4
				-4	0,3
					0,5
					0,5
					0,4
					0,4
		-60			0,2
				-7	0,3
		-20			0,4
		-70			0,5
					0,4
				-3	0,3
			-6		0,2
			-8		0,4
		-10			0,5
					0,2
				-7	0,3
					0,4
					0,,2
	-20		-2		0,3
	-30			-5	0,4
		-20			0,3
	-20				0,4
				-5	0,5

Додаток 3.

Задача 3. Визначення внутрішніх зусиль в статично невизначуваних плоскопросторових рамах та визначення розмірів поперечного перерізу

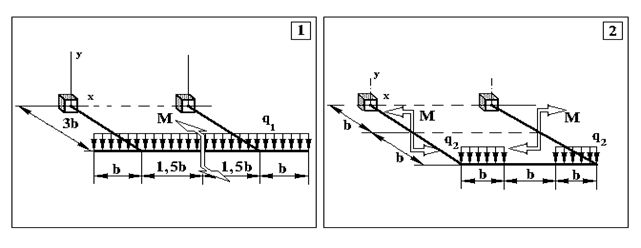
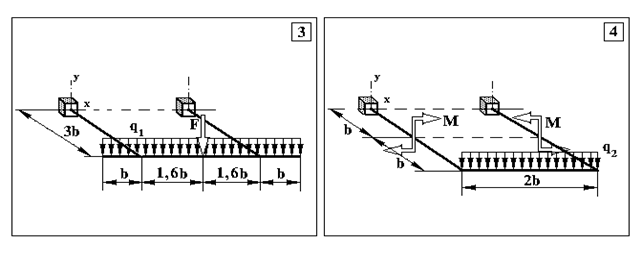
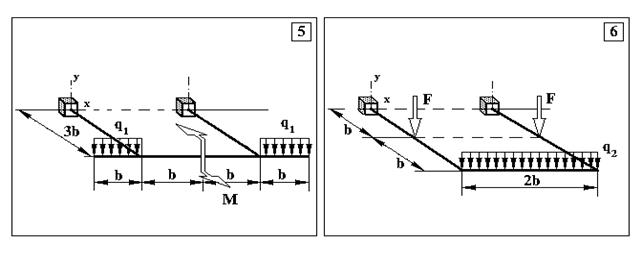
Продовження додатку 3.

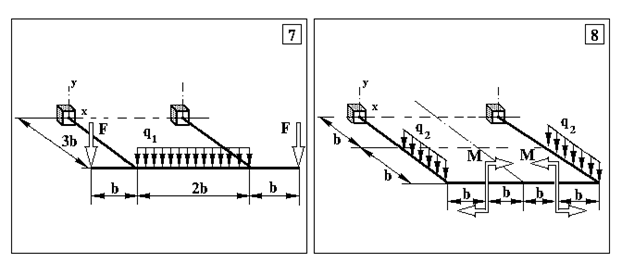
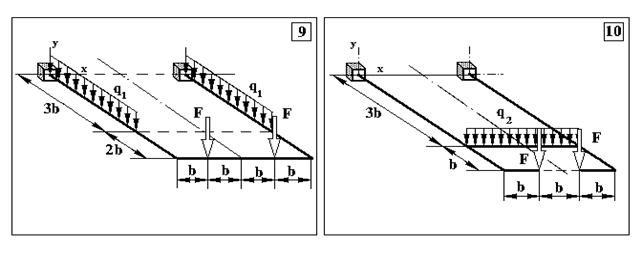
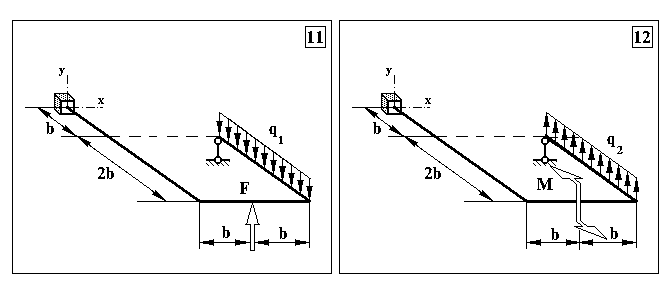
Продовження додатку 3.

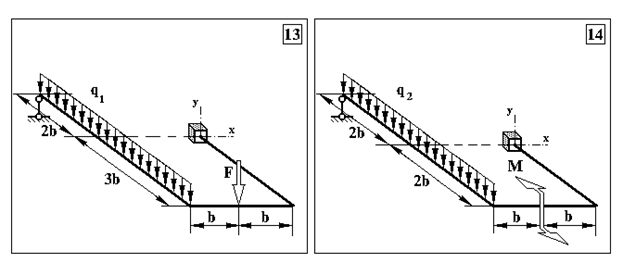
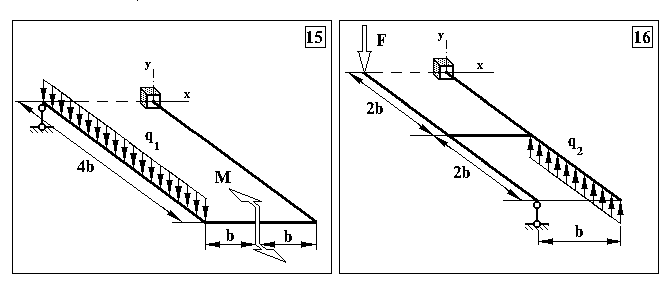
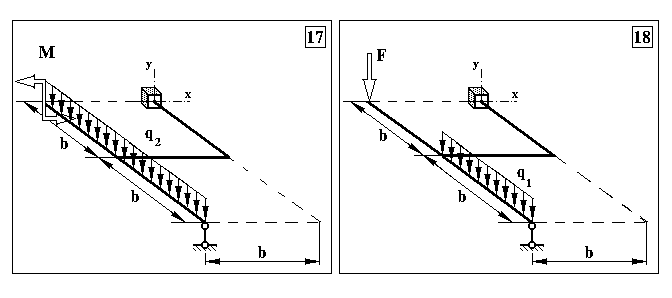
Продовження додатку 3.

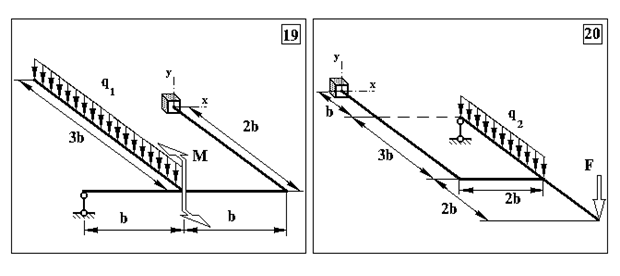
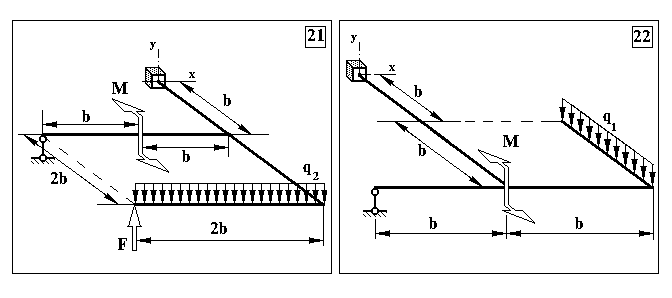
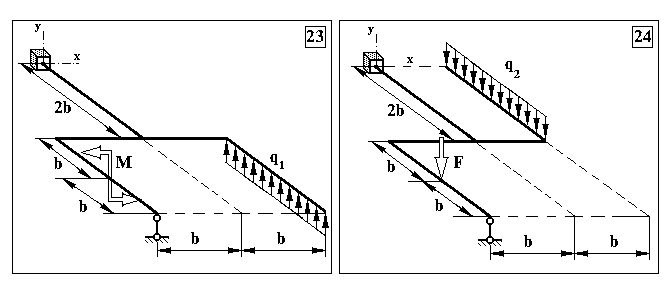
Таблиця Д.3.

Чисельні дані до задачі 3

№	q1, Н/м	q2 , Н/м	M , Нм	F, Н	Тип перерізу	sт, МПа	nт	b, м
							1,5	0,4
				-400			1,6	0,3
							1,8	0,5
							2,0	0,5
		-300					2,2	0,4
							2,4	0,4
		-300					2,5	0,2
				-800			1,4	0,3
		-200					1,5	0,4
		-200					1,6	0,5
							1,8	0,4
				-200			2,1	0,3
			-600				2,4	0,2
			-800				2,5	0,4
		-100					1,3	0,5
							1,5	0,2
				-600			1,8	0,3
							1,6	0,4
							2,5	0,,2
	-200		-200				2,4	0,3
	-300			-400			2,0	0,4
		-200					1,8	0,3
	-200						1,6	0,4
				-600			1,5	0,5

Додаток 4.

Типи перерізів до задачі 3

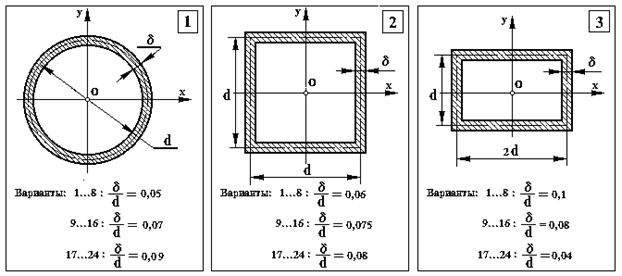
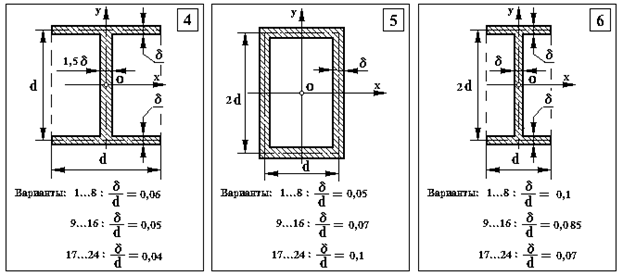
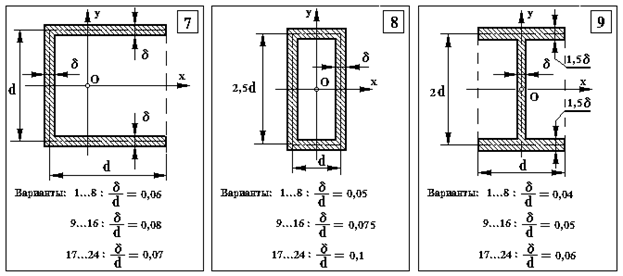
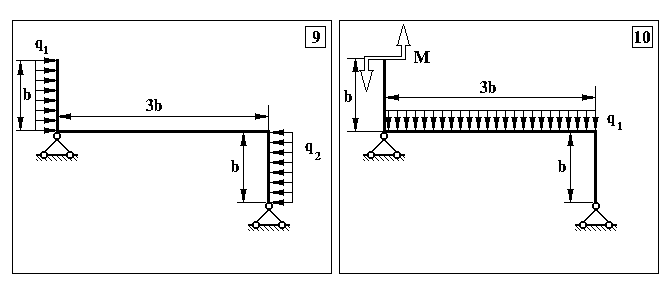
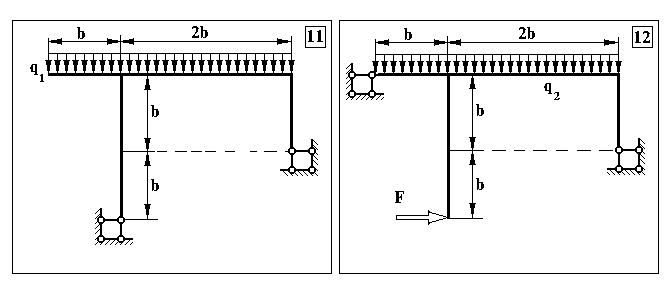
Додаток 5.

Контрольна задача № 4. (Для самостійної роботи)

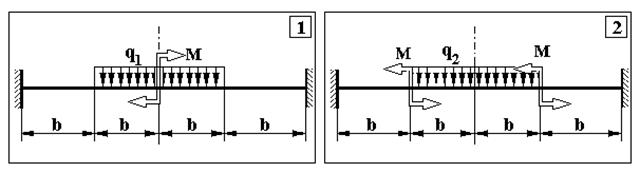
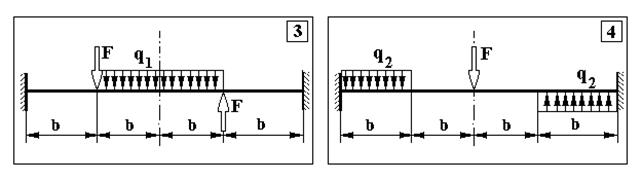
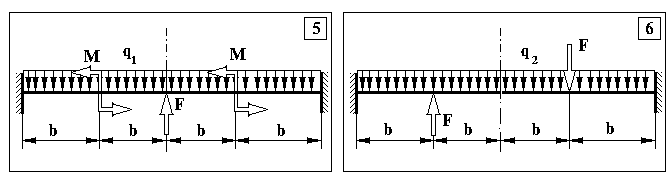
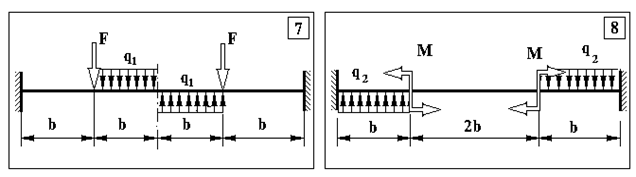
Продовження додатку 5.

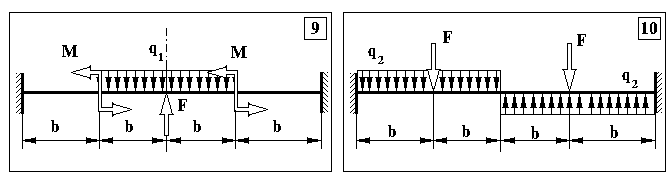
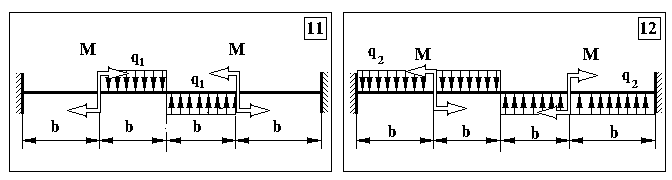
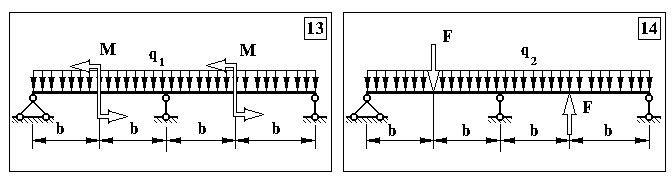
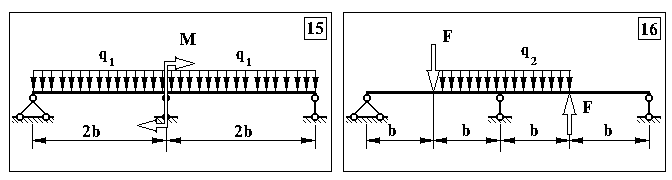
Продовження додатку 5.

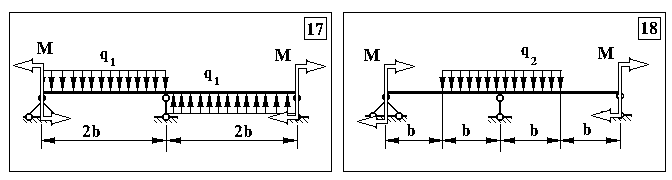
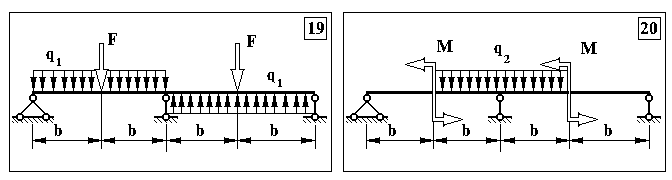
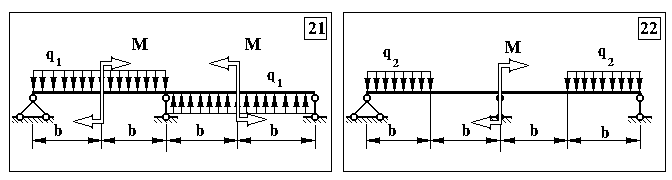
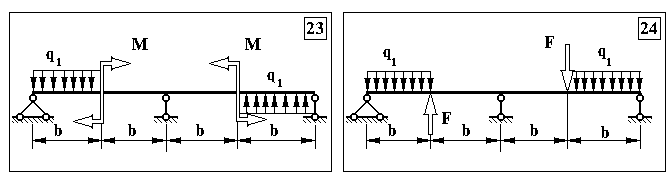
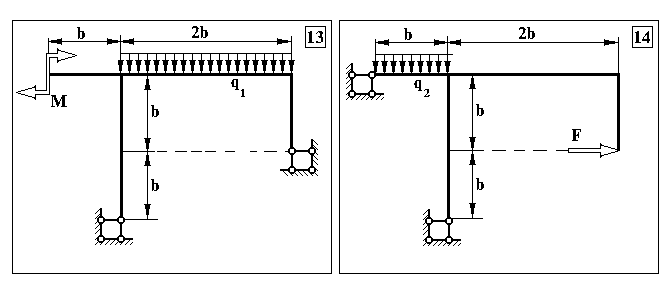
Додаток 6.

Контрольна задача № 5. (Для самостійної роботи)

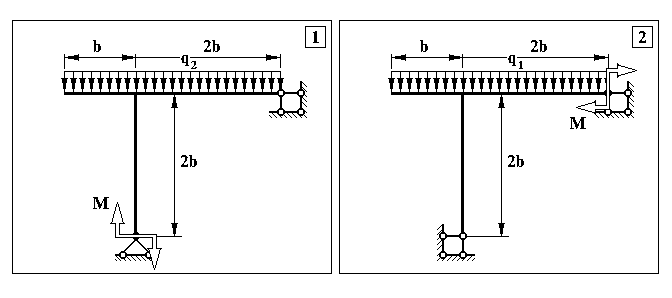
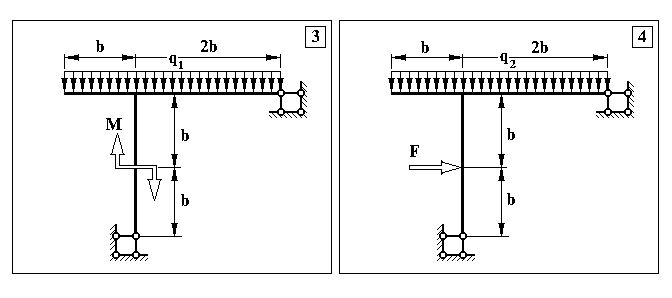
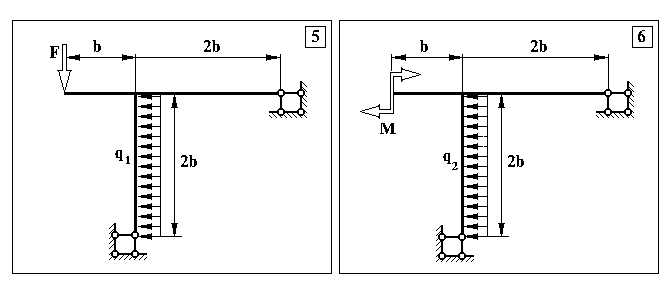
Продовження додатку 6.

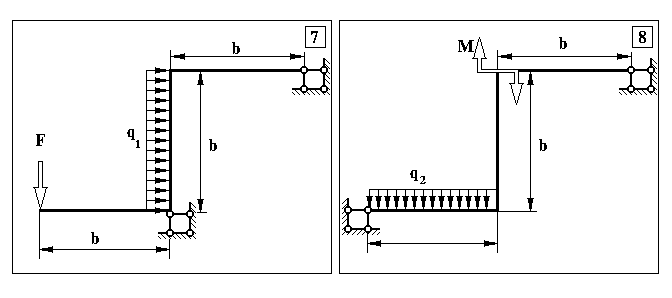
Продовження додатку 6.

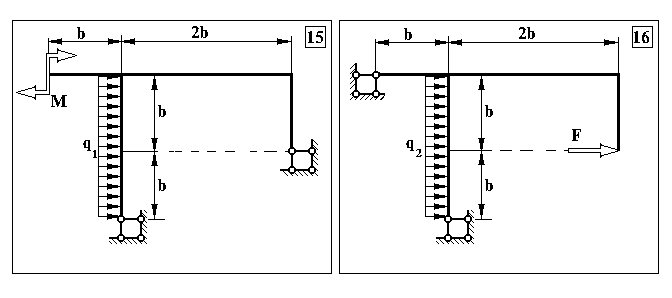
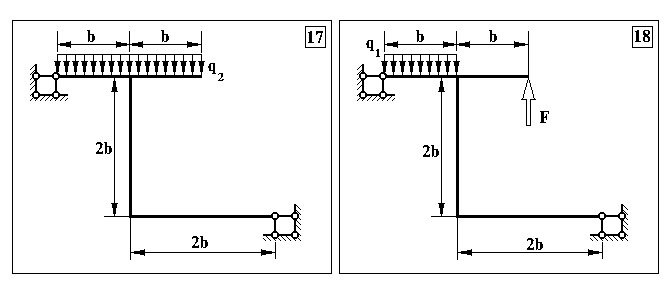
Продовження додатку 6.

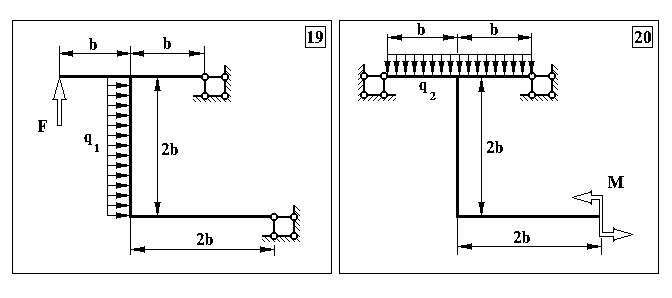
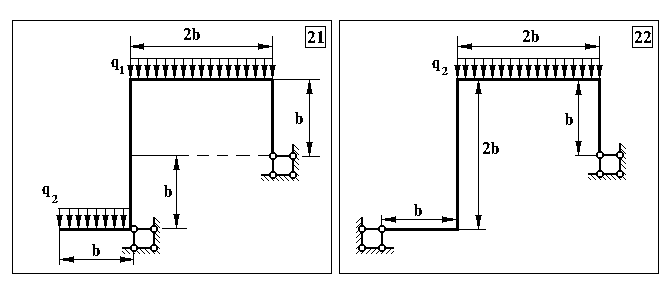
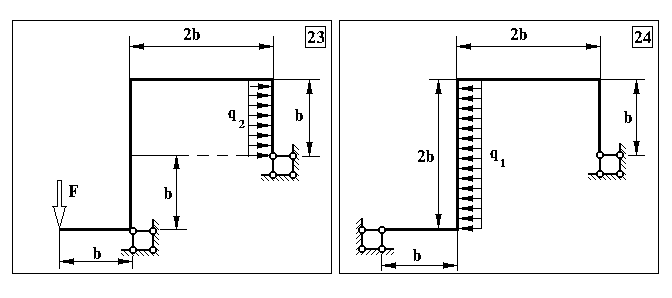
Таблиця Д.4.

Чисельні дані для контрольних задач №4, №5

№	q1, кН/м	q2 , кН/м	M , кНм	F, кН	b, м
1.					0,7
2.				-4	0,6
3.					0,8
4.					0,5
5.					0,6
6.					0,4
7.		-6			0,8
8.				-6	0,7
9.		-20			0,6
10.		-7			0,5
11.					0,4
12.				-8	0,3
13.			-6		0,7
14.			-8		0,8
15.	-7				0,5
16.					0,6
17.					0,7
18.				-10	0,4
19.					0,3
20.					0,8
21.		-9			0,6
22.	-15				0,7
23.				-4	0,4
24.					0,5

Зразок виконання розрахунку статично невизначуваної балки

Дано: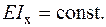

Необхідно:

- Розкрити статичну невизначуваність балки;

- Побудувати епюру згинаючого моменту.

Встановимо ступінь статичної невизначуваності системи.

.

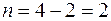При виборі основної статично визначуваної системи та відповідно до неї еквівалентної системи (рис. 30б,в) треба взяти до уваги умови симетрії заданої системи.

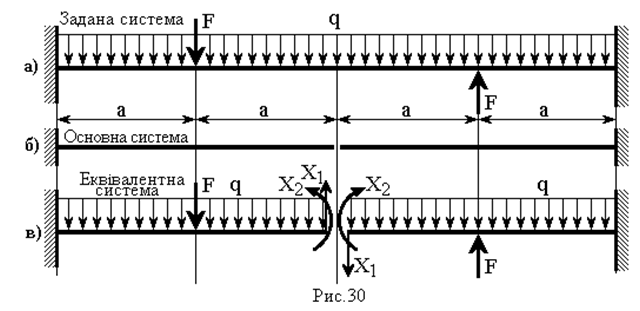Побудова епюр:

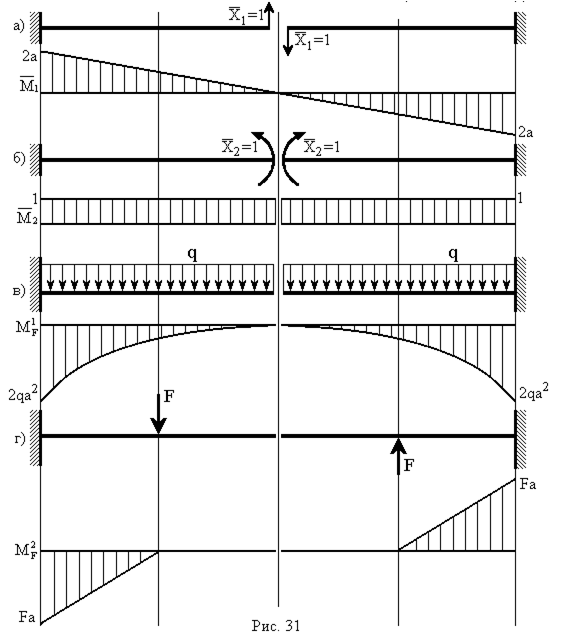
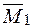– для схеми рис. 31а,

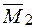– для схеми рис. 31б,

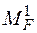– для схеми рис. 31в,

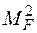– для схеми рис. 31г.

Канонічні рівняння методу сил мають вигляд:

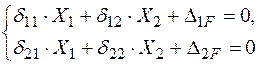
Визначення коефіцієнтів системи канонічних рівнянь методу сил.

;

;

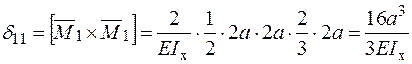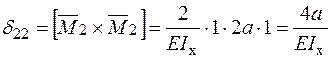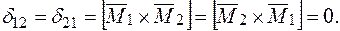
Визначення вантажних коефіцієнтів треба проводити для епюр згинаючих моментів, побудованих окремо для 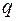(епюра 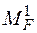) і для 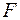(епюра ).

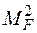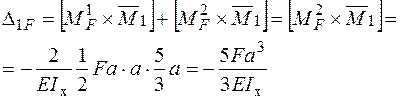
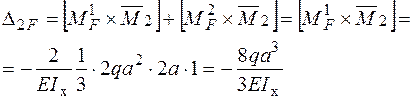
Рішення системи канонічних рівнянь метода сил:

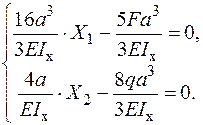
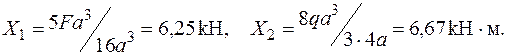
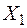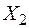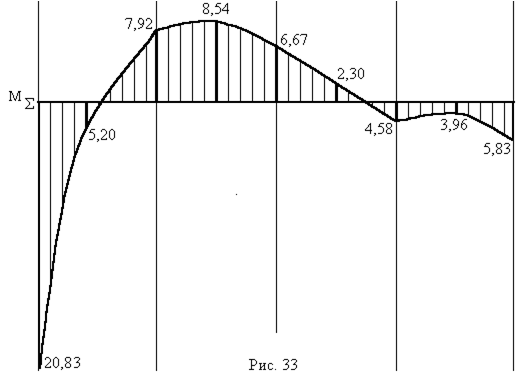
Будуємо епюри згинальних моментів від знайдених значень – (рис.32а), – (рис.32б) і сумарну епюру згинаючих моментів 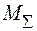– (рис. 33):

Перевірка виконання умов еквівалентності (канонічних рівнянь). При перемноженні епюр використовується спосіб Сімпсона – Карнаухова.

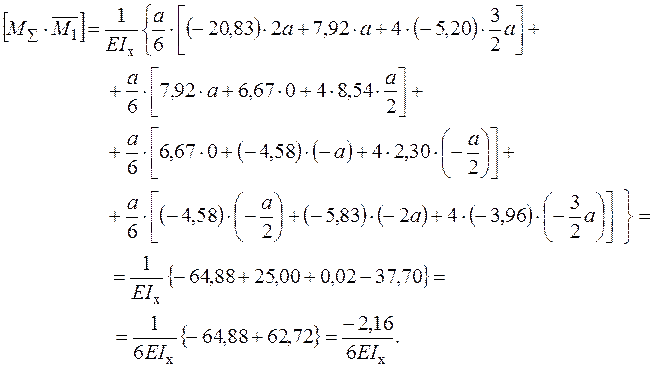
Відносна погрішність:

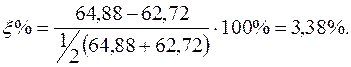
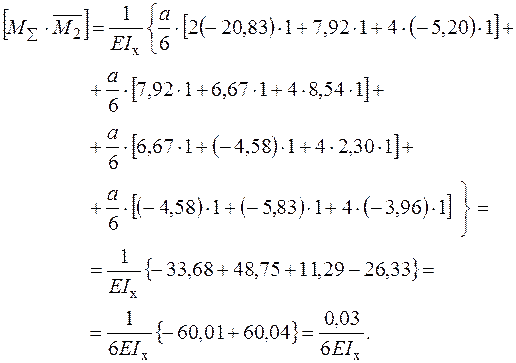
Відносна погрішність:

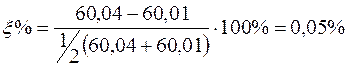
Зразок виконання розрахунку статично невизначуваної рами

Дано:

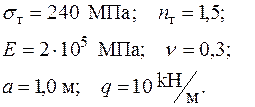
Необхідно:

- Розкрити статичну невизначуваність рами;

- Побудувати епюру згинаючого моменту.

Встановимо ступінь статичної невизначуваності системи.

.

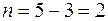Вибір основної статично визначуваної системи та відповідно до неї еквівалентної системи (рис. 34б,в) проводиться індивідуально.

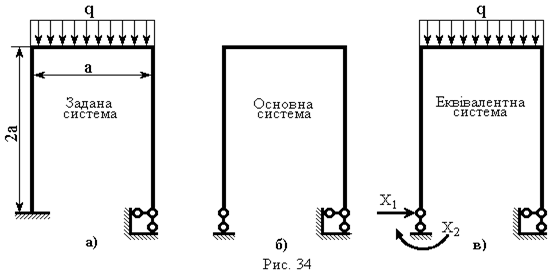Побудова епюр:

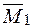– рис. 35а,

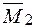– рис. 35б,

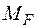– рис. 35в.

Канонічні рівняння методу сил мають вигляд:

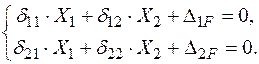
Визначення коефіцієнтів системи канонічних рівнянь методу сил.

;

;

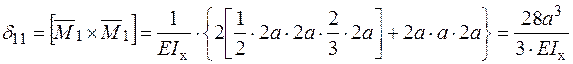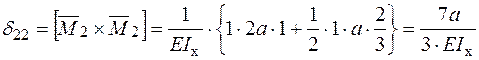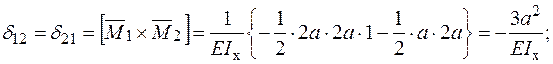
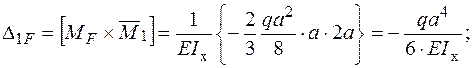
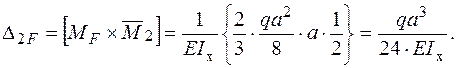
Рішення системи канонічних рівнянь метода сил:

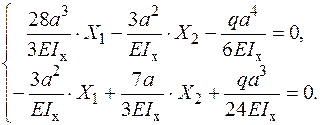
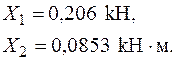
Будуємо епюри згинальних моментів від знайдених значень 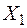– (рис.36а), 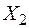– (рис.36б) і сумарну епюру згинаючих моментів 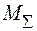(рис.36в):

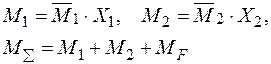
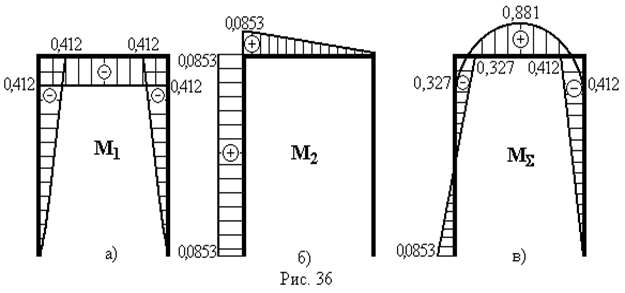Перевірка виконання умов еквівалентності (канонічних рівнянь).

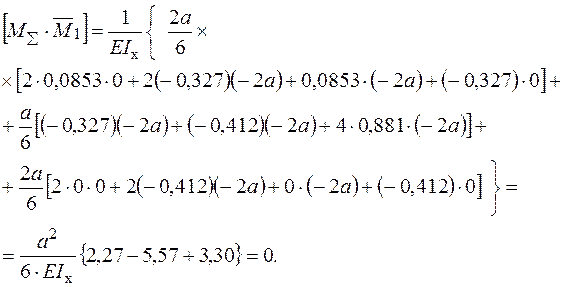
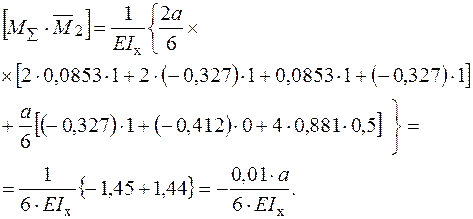
Відносна погрішність:

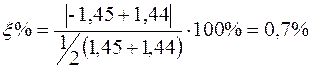
Зразок виконання розрахунку статично навизначуваної плоскопросторової рами

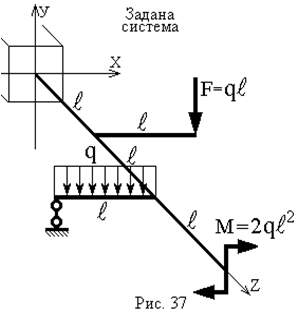Дано: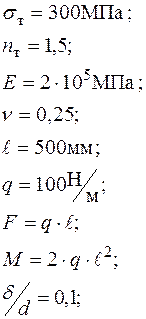

Необхідно:

- Розкрити статичну невизначуваність балки.

- Побудувати епюру згинаючого моменту.

- З умови міцності визначити розміри поперечного перерізу.

Встановимо ступінь статичної невизначуваності системи:

.

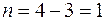Вибір основної статично визначуваної системи та відповідно до неї еквівалентної системи (рис. 39, 40) проводиться індивідуально.

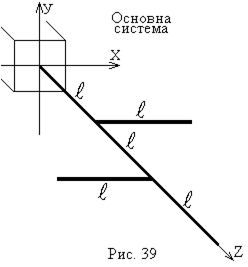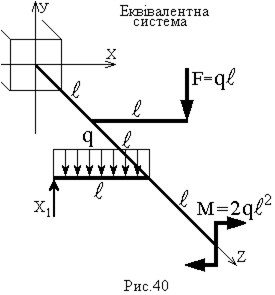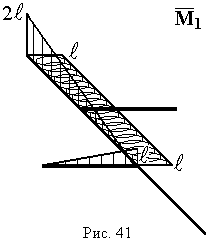
Побудова епюр: 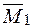– рис. 41, – рис. 42.

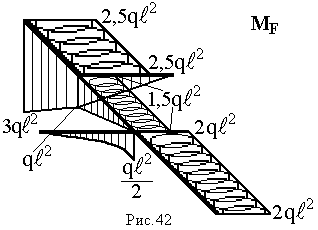Канонічні рівняння методу сил мають вигляд:

.

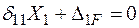Визначення коефіцієнтів системи канонічних рівнянь методу сил.

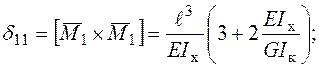
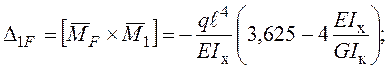
Визначення геометричних характеристик поперечного перерізу:

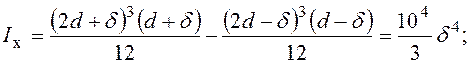
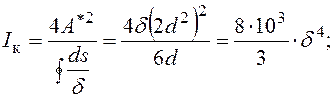
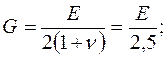
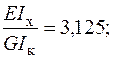
Остаточні значення питомих переміщень при цьому мають вигляд:

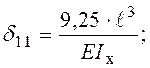
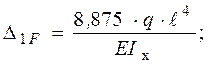
Рішення системи канонічних рівнянь метода сил:

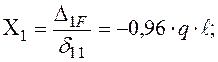
Будуємо сумарну епюру згинаючих моментів 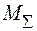(рис. 43):

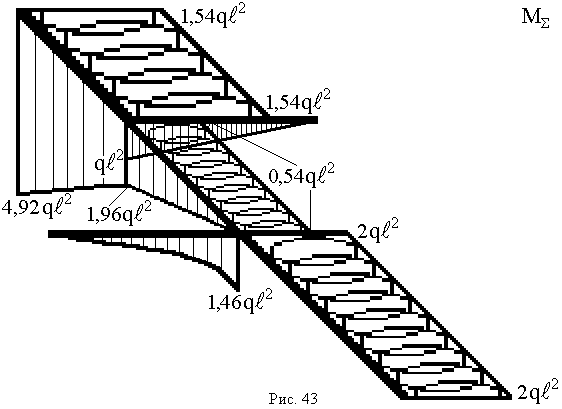Визначення геометричних розмірів небезпечного переріза.

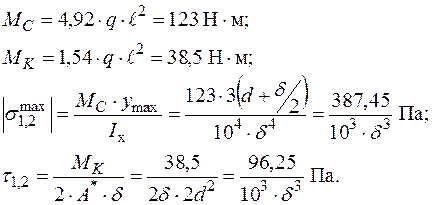Напружений стан у крайніх точках поперечного переріза:

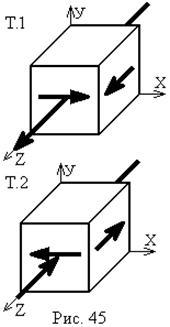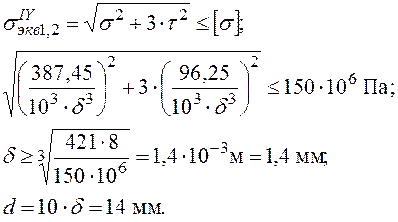Література

1. Писаренко Г.С., Квітка О.Л., Уманський Е.С. Опір матеріалів: Підручник. -К.: Вища школа, 1993.-655 с.: іл.

2. Феодосьев В. И. Сопротивление материалов. -М.: Наука, 1986.-512с.

Контрольні питання

1. Як визначити лінійне переміщення в точці?

2. Як визначити кутове переміщення в точці?

3. Що таке інтеграл Максвелла – Мора?

4. Як перемножуються епюри за способом Верещагіна?

5. Як перемножуються епюри за правилом трапецій?

6. Як перемножуються епюри за способом Сімпсона – Карнаухова?

7. Які системи називаються статично невизначуваними?

8. Що таке зайвий зв’язок і зайве невідоме зусилля?

9. Що називається ступенем статичної невизначуваності системи?

10. Який ступінь статичної невизначуваності замкненого контуру? Чому?

11. В якому порядку виконується розрахунок статично невизначуваних систем (методика розрахунку)?

12. Що таке метод сил?

13. Що таке основна система?

14. Що таке еквівалентна система?

15. Пояснити фізичний сенс коефіцієнтів канонічних рівнянь методу сил.

16. Якими прийомами можуть бути побудовані остаточні епюри внутрішніх зусиль?

17. Що слідує розуміти під раціональним вибором основної системи?

18. Які рами називаються симетричними і яким чином слідує вибирати в цьому випадку основну систему?

19. Які силові фактори симетричні?

20. Які силові фактори кососиметричні?

21. Яка рама називається плоскопросторовою?

22. Які внутрішні силові фактори є відмінними від нуля, якщо площина дії зовнішніх сил співпадає з площиною рами?

23. Які внутрішні силові фактори є відмінними від нуля, при дії зовнішніх сил перпендикулярних площині рами?

24. Яким чином визначаються переміщення в статично невизначуваних системах?

25. Сформулюйте, в чому полягає деформаційна перевірка правильності рішення статично невизначуваної задачі?

Навчальне видання

КОНОХОВ Володимир Іванович

ЛАВІНСЬКИЙ Володимир Іванович

ХАВІН Валерій Львович

Розрахунки статично невизначуваних стержньових систем методом сил.

Навчально – методичний посібник

з розділу курсу “Опір матеріалів”

для студентів машинобудівних спеціальностей.

Роботу до друку рекомендував С.К.Шелковий

Відповідальний за випуск В.В.Бортовий

В авторській редакції

План 2002р., п.151

Підп до друку 13.11.2002 р. Формат 60*84 1/16. Папір Morpa.

Друк - ризографія. Гарнітура Таймс. Умовн.-друк. арк. 4,0

Облік.-вид. арк. 4,2 Наклад 250 прим. Зам. № 460. Ціна договірна

Видавничий центр НТУ “ХПІ”. Свідоцтво ДК №116 від 10.07.2000р. 61002, Харків, вул. Фрунзе, 21

Друкарня НТУ “ХПІ”