Метод зон Френеля. Прямолінійне поширення світла

За допомогою принципу Гюйгенса-Френеля можна обґрунтувати з хвильових властивостей світла закон прямолінійного поширення світла в однорідному середовищі. Френель розв’язав цю задачу, розглянувши взаємну інтерференцію вторинних хвиль, і застосував прийом, який отримав назву методу зон Френеля.

Знайдемо в довільній точці М амплітуду світлової хвилі, що поширюється в однорідному середовищі від точкового джерела .

Згідно з принципом Гюйгенса-Френеля замінимо дію джерела дією уявних джерел, які розміщені на допоміжній поверхні S, що є однією з хвильових поверхонь хвилі, яка поширюється від джерела (рис. 222).

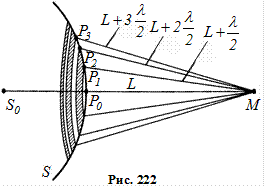
Ця допоміжна поверхня є поверхнею сфери з центром в . Френель розбив хвильову поверхню S на кільцеві зони такого розміру, щоб відстані від країв зони до М відрізнялись на 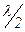, тобто

.

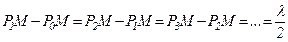Подібне розбивання хвильової поверхні S на зони можна виконати, провівши з точки М концентричні сфери радіусами

; ; ; ... .

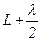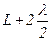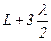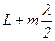Точки сфери S, що лежать від точки М на відстанях 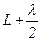; ; 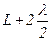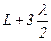і т.д. утворюють межі 1-ї, 2-ї, 3-ї і т.д. зон Френеля.

Оскільки коливання від сусідніх зон проходять до точки М відстані, які відрізняються на 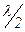, то в точку М вони надходять з протилежними фазами і при накладанні ці коливання будуть взаємно ослаблюватися. Тому амплітуда результуючого коливання в точці М

,

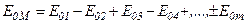де 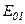, , 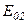… - амплітуди коливань, що збуджуються 1-ю, 2-ю,…, m-ю зонами. В цей вираз всі амплітуди коливань від непарних зон входять зі знаком „+”, а від
парних зон – зі знаком „–”.

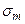Величина залежить від площі m-ї зони і кута 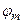між зовнішньою нормаллю до поверхні зони в якій-небудь її точці і прямою, яка напрямлена з цієї
точки в точку М. На рис. 223 точки В і 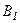відповідають зовнішній границі m-ї зони; 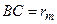– радіус зовнішньої границі m-ї зони, 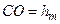– висота кульового сегмента .

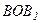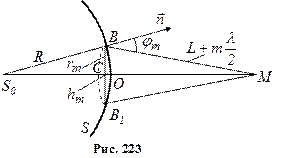
З трикутників 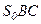і MBC видно, що

.

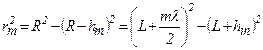Звідси

.

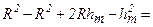
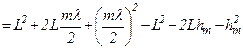Тоді

.

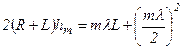Оскільки 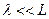, то при не дуже великих m доданком 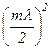можна знехтувати і

.

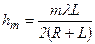Бічна поверхня кульового сегмента 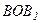, яка є сумою площ усіх m зон, починаючи з першої, дорівнює

,

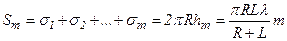а площа m-ї зони Френеля

.

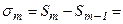
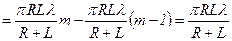Цей вираз не залежить від m, отже, при не дуже великих m площі зон Френеля однакові. У такий спосіб побудова зон Френеля розбиває поверхню сферичної хвилі на рівні за площею зони.

Із збільшенням номера зони m зростають кут 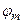і відстань від зони до точки М. Згідно із принципом Гюйгенса-Френеля це приводить до монотонного зменшення інтенсивності випромінювання в напрямку точки M. Тому

.

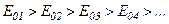Загальне число N зон Френеля, які вміщуються на частині сфери, яка повернена до точки М (рис. 224), дуже велике.

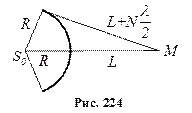
З рис. 224 видно, що

.

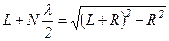Звідси:

.

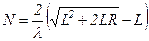Якщо R=L=0,1 м і 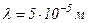, то 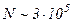. Тому можна вважати, що в межах не дуже великих змін m залежність від m є лінійною, і амплітуда коливань, яка викликана якою-небудь m-ю зоною, дорівнює півсумі амплітуд коливань, що викликан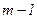і -ю і 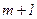-ю зонами. Тобто

.

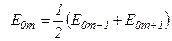Тоді амплітуда результуючого коливання в точці М матиме такий вигляд:

,

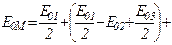
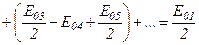оскільки усі вирази, що стоять у дужках, дорівнюють нулю. Отже, амплітуда коливань, що створюється в довільній точці М сферичною хвильовою поверхнею, дорівнює половині амплітуди коливань, що створюється однією центральною зоною. Дія всієї хвильової поверхні на точку М зводиться до дії її малої ділянки, меншої, ніж центральна зона.

Якщо у виразі 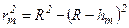покладемо, що висота сегмента 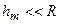(при не дуже великих m), тоді 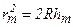. Радіус зовнішньої границі m-ї зони Френеля

.

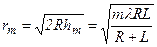При R=L=0,1м і =0,5мкм 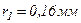. Отже, поширення світла від до М відбувається так, немовби світловий потік поширюється всередині дуже вузького каналу вздовж M, тобто прямолінійно. У такий спосіб хвильовий принцип Гюйгенса-Френеля дозволяє пояснити прямолінійне поширення світла в однорідному середовищі.

Виразимо кількість зон Френеля m через радіус зовнішньої границі:

.

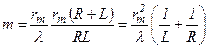Кількість зон m симетричне відносно L і R. Це означає, що точкове джерело викликає в точці M таку дію, яку викликало б у точці , якщо його розмістити у точці M.

Інтенсивність світла в точці M можна значно збільшити, якщо закрити всі
парні або непарні зони Френеля. Тоді результуюча амплітуда коливань відповідно дорівнюватиме:

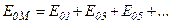
або

.

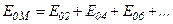Екран, який перекриває всі парні або непарні зони Френеля, називається зонною пластинкою. Пластинка має складатися з прозорих або непрозорих кілець, радіуси яких дорівнюють 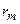. Радіуси прозорих кілець підраховують для m=0, 2, 4,…, непрозорих – для m=1, 3, 5,….

УМОВ МИКОЛА ОЛЕКСІЙОВИЧ

(1846-1915)

Розробив оригінальний метод обчислення інтегралів О.Френеля, які мають велике значення в теорії дифракції.