Причинность, регрессия, корреляция

Статистическое изучение взаимосвязи социально-экономических явлений

Причинность, регрессия, корреляция

Исследование объективно существующих связей между явлениями – важнейшая задача общей теории статистики. В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие существенное влияние на вариацию изучаемых явлений и процессов. Причинно-следственные отношения – это связь явлений и процессов, когда изменение одного из них – причины – ведет к изменению другого – следствия.

Социально-экономические явления представляют собой результат одновременного воздействия большого числа причин. Следовательно, при изучении этих явлений необходимо выявлять главные, основные причины, абстрагируясь от второстепенных.

Статистика разработала множество методов изучения связей, выбор которых зависит от целей исследования и от поставленных задач. Признаки по их значению для изучения взаимосвязи делятся на два класса. Признаки, обуславливающие изменения других, связанных с ними признаков, называются факторными, или просто факторами. Признаки, изменяющиеся под действием факторных признаков, являются результативными.

Связи между явлениями и их признаками классифицируются по степени тесноты связи, направлению и аналитическому выражению.

В статистке различают функциональную связь и стохастическую зависимость. Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака. Функциональная связь проявляется во всех случаях наблюдения и для каждой конкретной единицы исследуемой совокупности.

Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений, то такая зависимость называется стохастической. Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.

По направлению выделяют связь прямую и обратную. При прямой связи с увеличением или уменьшением значений фактурного признака происходит увеличение или уменьшение значений результативного. Так, например, рост производительности труда способствует увеличению уровня рентабельности производства. В случае обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением факторного признака. Так, с увеличением уровня фондоотдачи снижается себестоимость единицы производимой продукции

По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и нелинейные. Если статистическая связь между явлениями может быть приближенно выражена уравнением прямой линии, то ее называют линейной связью, если же она выражается уравнением какой-либо кривой линии (параболы, гиперболы, степенной, показательной, экспоненциальной и т.д.), то такую связь называют нелинейной или криволинейной.

Дли социально-экономических явлений характерно, что наряду с существенными факторами, формирующими уровень результативного признака, на него оказывают действие многие другие неучтенные и случайные факторы. Это свидетельствует о том, что взаимосвязи явлений, которые изучает статистика, носят корреляционный характер и аналитически выражаются функцией вида .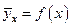

Корреляция – это статистическая зависимость между случайными величинами, не имеющая строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математическою ожидания другой.

В статистике принято различать следующие виды зависимостей:

1) парная корреляция – связь между двумя признаками (результативным и факторным или двумя факторными);

2) частная корреляция – зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков;

3) множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование.

Корреляционная зависимость исследуется с помощью методов корреляционного и регрессионного анализов.

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).

Теснота связи количественно выражается величиной коэффициентов корреляции. Коэффициенты корреляции, представляя количественную характеристику тесноты связи между признаками, дают возможность определять «полезность» факторных признаков при построении уравнения множественной регрессии. Величина коэффициента корреляции служит также оценкой соответствия уравнения регрессии выявленным причинно-следственным связям.

Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины, называемой зависимой или результативным признаком, обусловлено влиянием одной или нескольких независимых величин (факторов), а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения. Регрессия может быть однофакторной (парной) и многофакторной (множественной).

Основной предпосылкой регрессионного анализа является то, что только результативный признак 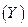подчиняется нормальному закону распределения, а факторные признаки 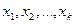могут иметь произвольный закон распределения. В анализе динамических рядов в качестве факторного признака выступает время 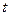. При этом в регрессионном анализе заранее подразумевается наличие причинно-следственных связей между результативным 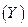и факторными 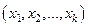признаками.

Уравнение регрессии, или статистическая модель связи социально-экономических явлений, выражаемая функцией 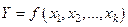, является достаточно адекватным реальному моделируемому явлению или процессу в случае соблюдения следующих требований их построения:

1.Совокупность исследуемых исходных данных должна быть однородной и математически описываться непрерывными функциями.

2.Возможность описания моделируемого явления одним или несколькими уравнениями причинно-следственных связей.

3.Все факторные признаки должны иметь количественное (цифровое) выражение.

4.Наличие достаточно большого объема исследуемой выборочной совокупности.

5.Отсутствие количественных ограничений на параметры модели связи.

6.Постоянство территориальной и временной структуры изучаемой совокупности.

Соблюдение данных требований позволяет исследователю построить статистическую модель связи, наилучшим образом аппроксимирующую моделируемые социально-экономические явления и процессы.

Одной из проблем построения уравнения регрессии является ее размерность, т. е. определение числа факторных признаков, включаемых в модель. Их число должно быть оптимальным. Сокращение размерности за счет исключения второстепенных, несущественных факторов позволяет получить модель, быстрее и качественнее реализуемую. Однако построение модели малой размерности может привести к тому, что она будет недостаточно полно описывать исследуемое явление или процесс.

Практика выработала определенный критерий, позволяющий установить оптимальное соотношение между числом факторных признаков, включаемых в модель, и объемом исследуемой совокупности. Согласно данному критерию число факторных признаков 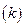должно быть в 5 – 6 раз меньше объема изучаемой совокупности.

Корреляционно-регрессионный анализ как общее понятие включает в себя измерение тесноты, направления связи и установление аналитического выражения связи.