Лекція 6. ПОХІДНА І ДИФЕРЕНЦІАЛ

Задачі, що приводять до поняття похідної

Поняття похідної є одним з основних математичних понять. Похідна широко використовується при розв’язуванні цілої низки задач математики, фізики, економіки, інших наук. Необхідність у використанні похідної виникає тоді, коли ставиться задача, наприклад, визначити швидкість протікання процесів, побудувати функцію, що приблизно описує поведінку заданої, обчислити похибки вимірювань.

Швидкість прямолінійного руху

Нехай матеріальна точка (деяке тіло) М рухається нерівномірно по деякій прямій. Кожному значенню часу t відповідає певна відстань ОМ = S до деякої фіксованої точки О. Цявідстань залежить від часу t, що минув, тобто S= S(t).

Цю рівність називають законом руху точки. Необхідно знайти швидкість руху точки.

Якщо в деякий момент часу t точка займає положення М, то у момент часу t+∆t (∆t – приріст часу) точка займе положення M₁, де ОM₁ =S+∆S (∆S – приріст відстані). Таким чином, переміщення точки М за час ∆t буде ∆S = S(t + ∆t) – S(t).

Відношення 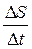виражає середню швидкість руху точки за час ∆t:

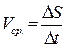
Середня швидкість залежить від значення ∆t: чим менше ∆t, тим точніше середня швидкість виражає швидкість руху точки в даний момент часу t.

Межа середньої швидкості руху при прагненні до нуля проміжку часу ∆t називається швидкістю руху точки в даний момент часу (або миттєвою швидкістю). Позначивши цю швидкість через V, отримаємо

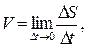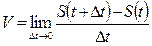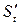або = (2.10)

Дотична до кривої

Дамо спочатку загальне визначення дотичної до кривої.

Візьмемо на неперервній кривій L дві точки М і М₁ (див. рис. 2.5).

Пряму M M₁, що проходить через ці точки, називають січною.

Нехай точка М₁, рухаючись уздовж кривої L, необмежено наближається до точки М. Тодісічна, повертаючись біля точки М, прямує до деякого граничного положення МТ.

Дотичною до даної кривої в даній точці М називається граничне положення МТ січної MM₁, що проходить через точку М, коли друга точка перетину M₁ необмежено наближається по кривій до точки M.

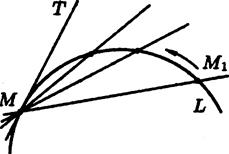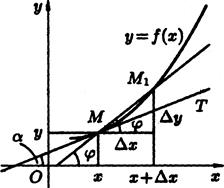Рис. 2.5	Рис. 2.6

Розглянемо тепер графік неперервної кривої у = f(x), який має в точці М (х;у) невертикальну дотичну. Знайдемо її кутовий коефіцієнт, 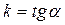, де a – кут дотичної з віссю Ох.

Для цього проведемо через точку М і точку M₁ графіка з абсцисою х+∆х січну (див. рис. 2.6). Позначимо через j — кут між січною MM₁ і віссю Ох. На рисунку видно, що кутовий коефіцієнт січної дорівнює

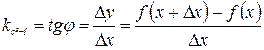
При 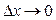через неперервність функції приріст ∆y теж прямує до нуля; тому точка M₁ необмежено наближається по кривій до точки М, а січна MM₁, повертаючись біля точки М, переходить в дотичну. Кут, 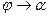тобто 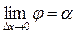. Звідси отримуємо геометричний зміст похідної

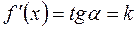(2.11)