Законы сохранения. закон сохранения момента импульса
Основные формулы
Момент импульса вращающегося тела 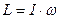
Закон сохранения момента импульса 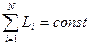 , где
, где 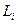 - момент импульса
- момент импульса 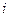 -го тела, входящего в состав системы.
-го тела, входящего в состав системы.
Закон сохранения импульса для двух взаимодействующих тел 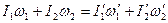 , где
, где 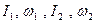 - моменты инерции и угловые скорости тел дл взаимодействия,
- моменты инерции и угловые скорости тел дл взаимодействия, 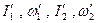 - те же величины после взаимодействия
- те же величины после взаимодействия
Закон сохранения момента импульса для одного тела, момент инерции которого изменяется 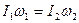 , где
, где 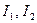 - начальный и конечный моменты инерции;
- начальный и конечный моменты инерции; 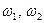 - начальная и конечная угловые скорости тела.
- начальная и конечная угловые скорости тела.
Работа постоянного момента силы  , действующего на вращающееся тело
, действующего на вращающееся тело 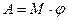 , где
, где 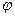 -угол поворота тела.
-угол поворота тела.
Кинетическая энергия вращающегося тела 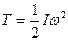
Кинетическая энергия тела, катящегося по плоскости без скольжения равна сумме кинетической энергии поступательного движения 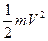 и кинетической энергии вращения
и кинетической энергии вращения 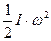
Работа, совершаемая при вращении тела, и изменение кинетической энергии связаны соотношением 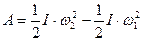
Кинетическая энергия вращающегося тела 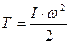 .
.
Момент импульса вращающегося тела относительно оси 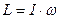 .
.
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Запишите формулу для работы постоянного момента силы, действующего на вращающееся тело.
2. Запишите формулу для кинетической энергии тела, катящегося по плоскости без скольжения.
3. Величины, характеризующие динамику вращательного движения, и формулы, описывающие это движение, аналогичны соответствующим величинам и формулам поступательного движения. Раскройте эту аналогию с помощью таблицы. (в строчках 1-5 написать обозначение или формулу)
| Поступательное движение | Вращательное движение |
| перемещение | Поворот |
| скорость | Угловая скорость |
| ускорение | Угловое ускорение |
| масса | Момент инерции |
| импульс | Момент импульса |
| Основной закон динамики | |
| Закон сохранения | |
| Работа и мощность | |
| Кинетическая энергия | |
ЗАДАЧИ
1. Стержень длиной 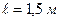 и массой
и массой 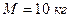 может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня. В середину стержня ударяет пуля массой
может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня. В середину стержня ударяет пуля массой 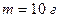 , летящая в горизонтальном направлении со скоростью
, летящая в горизонтальном направлении со скоростью 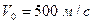 , и застревает в нем. На какой угол отклонится стержень после удара?
, и застревает в нем. На какой угол отклонится стержень после удара?
2. Шар катится без скольжения по горизонтальной поверхности. Полная кинетическая энергия шара равна 14 Дж. Определите кинетическую энергию поступательного и вращательного движения шара.
3. Шар диаметром 6 см катится без скольжения по горизонтальной плоскости с частотой  . Масса шара равна 0,25 кг. Найти кинетическую энергию шара.
. Масса шара равна 0,25 кг. Найти кинетическую энергию шара.
4. Определить линейную скорость шара, скатившегося без скольжения с наклонной плоскости высотой 1 м.
5. Твердый цилиндр массы 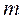 скатывается без скольжения по наклонной плоскости длиной
скатывается без скольжения по наклонной плоскости длиной  , наклоненной под углом
, наклоненной под углом 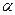 к горизонту. Чему равна скорость цилиндра в нижней части наклонной плоскости? Трением пренебречь.
к горизонту. Чему равна скорость цилиндра в нижней части наклонной плоскости? Трением пренебречь.
6. Обруч и сплошной цилиндр, имеющие одинаковую массу 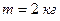 , катятся без скольжения с одинаковой с одинаковой скоростью
, катятся без скольжения с одинаковой с одинаковой скоростью  . Найти кинетическую энергию этих тел.
. Найти кинетическую энергию этих тел.
7. Сплошной цилиндр массой 4 кг катится без скольжения по горизонтальной поверхности. Линейная скорость оси цилиндра 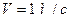 . Определить полную кинетическую энергию цилиндра.
. Определить полную кинетическую энергию цилиндра.
8. Платформа в виде диска радиусом 1,5 м и массой 180 кг вращается по инерции вокруг вертикальной оси с частотой 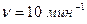 . В центре платформы стоит человек массой 60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?
. В центре платформы стоит человек массой 60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?
9. На краю горизонтальной платформы, имеющей форму диска радиусом 2 м, стоит человек массой 80 кг. Масса платформы 240 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью будет вращаться платформа, если человек будет идти вдоль платформы со скоростью 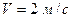 относительно платформы.
относительно платформы.
10. Кинетическая энергия вращающегося маховика равна 1 кДж. Под действием постоянного тормозящего момента маховик начал вращаться равнозамедленно и, сделав 80 оборотов, остановился. Определить момент силы торможения.
11. Кинетическая энергия вала, вращающегося с постоянной скоростью, соответствующей 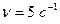 , равна 60 Дж. Найти момент количества движения этого вала.
, равна 60 Дж. Найти момент количества движения этого вала.
12. Медный шар радиусом 10 см вращается с угловой скоростью  . Какую работу надо совершить, чтобы увеличить угловую скорость вращения шара вдвое?
. Какую работу надо совершить, чтобы увеличить угловую скорость вращения шара вдвое?
13. Карандаш, поставленный вертикально, падает на стол. Какую угловую и линейную скорость будет иметь в конце падения середина карандаша? Длина карандаша 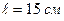 .
.
14. 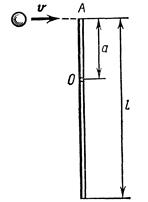 Медный шар радиусом 10 см вращается со скоростью, соответствующей
Медный шар радиусом 10 см вращается со скоростью, соответствующей  , вокруг оси, проходящей через его центр. Какую работу надо совершить, чтобы увеличить угловую скорость вращения шара вдвое?
, вокруг оси, проходящей через его центр. Какую работу надо совершить, чтобы увеличить угловую скорость вращения шара вдвое?
15. Однородный тонкий стержень массой 0,2 кг и длиной 1 м может свободно вращаться вокруг горизонтальной оси z , проходящей через точку О. В точку А на стержне попадает пластилиновый шарик, летящий горизонтально (перпендикулярно оси z) со скоростью 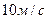 и прилипает к стержню. Масса шарика равна 10 г. Определить угловую скорость стержня и линейную скорость нижнего конца стержня в начальный момент времени. Расстояние между точками А и О равно
и прилипает к стержню. Масса шарика равна 10 г. Определить угловую скорость стержня и линейную скорость нижнего конца стержня в начальный момент времени. Расстояние между точками А и О равно 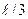 .
.
16. Шарик массой 100 г, привязанный к концу нити длиной 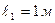 , вращается, опираясь на горизонтальную плоскость с частотой 1 Гц. Нить укорачивается и шарик приближается к оси вращения до расстояния
, вращается, опираясь на горизонтальную плоскость с частотой 1 Гц. Нить укорачивается и шарик приближается к оси вращения до расстояния 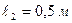 . С какой частотой при этом будет вращаться шарик? Какую работу совершит внешняя сила? Трением пренебречь.
. С какой частотой при этом будет вращаться шарик? Какую работу совершит внешняя сила? Трением пренебречь.
17. Маховик вращается по закону, выражаемому уравнением 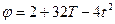 . Найти среднюю мощность, развиваемую силами, действующими на маховик при его вращении, до остановки, если его момент инерции
. Найти среднюю мощность, развиваемую силами, действующими на маховик при его вращении, до остановки, если его момент инерции  .
.
18. .Частота вращения маховика, момент инерции которого равен 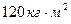 , составляет
, составляет 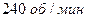 . После прекращения действия на него вращающего момента маховик под действием сил трения в подшипниках остановился за время
. После прекращения действия на него вращающего момента маховик под действием сил трения в подшипниках остановился за время 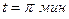 . Считая трение в подшипниках постоянным, определите момент сил трения.
. Считая трение в подшипниках постоянным, определите момент сил трения.
19. К ободу однородного сплошного диска массой 10 кг, насаженного на ось, приложена постоянная касательная сила 30 Н. Определите кинетическую энергию через время 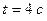 после начала действия силы.
после начала действия силы.
20. Полый тонкостенный цилиндр массой 0,5 кг, катящийся без скольжения, ударяется о стену и откатывается от нее. Скорость цилиндра до удара 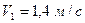 , после удара
, после удара 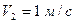 . Определите выделившееся при ударе количество теплоты.
. Определите выделившееся при ударе количество теплоты.
Семинар 11
Кинематика колебаний
Основные формулы
Кинематические характеристики колебательного движения:
Уравнение гармонических колебаний (путь, смещение) 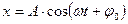 , где
, где
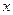 - смещение колеблющейся точки от положения равновесия;
- смещение колеблющейся точки от положения равновесия; 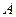 - амплитуда колебаний ( максимальное отклонение от положения равновесия);
- амплитуда колебаний ( максимальное отклонение от положения равновесия); 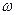 -угловая частота;
-угловая частота; 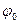 - начальная фаза колебаний;
- начальная фаза колебаний; 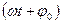 - фаза колебаний в момент времени
- фаза колебаний в момент времени 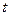 .
.
Скорость точки, совершающей гармонические колебания 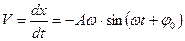
Ускорение при гармонических колебаниях 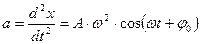
Угловая частота колебаний 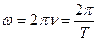 , где
, где 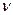 и
и  - частота и период колебаний
- частота и период колебаний
Динамические характеристики колебательного движения:
Сила- 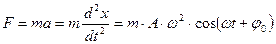
Кинетическая энергия 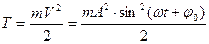
Потенциальная энергия 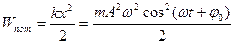
Полная энергия 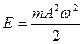
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Зависимость от времени координаты некоторой системы с одной степенью свободы имеет вид 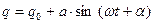 . Какое движение совершает эта система? Перечислите его основные параметры.
. Какое движение совершает эта система? Перечислите его основные параметры.
2. Зависимость от времени координаты некоторой системы с одной степенью свободы имеет вид: 1) 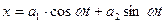 ; 2)
; 2) 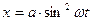 ; 3)
; 3) 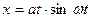 ; 4)
; 4) 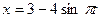 , Какие из зависимостей описывают гармонические колебания? Определите для этих случаев значения
, Какие из зависимостей описывают гармонические колебания? Определите для этих случаев значения 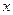 , соответствующих положению равновесия, амплитуду, частоту и начальную фазу колебаний.
, соответствующих положению равновесия, амплитуду, частоту и начальную фазу колебаний.
3. Уравнение колебаний задано в виде 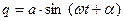 . Чему равны: а) сила, действующая на частицу при прохождении положения равновесия; б) ее скорость в тот момент, когда она находится в «крайнем» положении.
. Чему равны: а) сила, действующая на частицу при прохождении положения равновесия; б) ее скорость в тот момент, когда она находится в «крайнем» положении.
4. Энергия одномерного гармонического осциллятора имеет вид 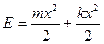 , где
, где 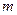 - масса,
- масса, 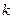 - коэффициент упругости. Найти амплитуду колебаний и амплитуду скорости.
- коэффициент упругости. Найти амплитуду колебаний и амплитуду скорости.
5. Частица массы 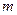 совершает гармонические колебания вдоль оси
совершает гармонические колебания вдоль оси 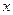 около точки
около точки 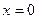 с частотой
с частотой 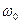 . В начальный момент времени
. В начальный момент времени 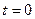 ее координата и скорость соответственно равны: а)
ее координата и скорость соответственно равны: а) 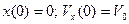 ; б)
; б) 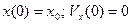 ; в)
; в) 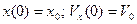 . Определите для этих трех случаев полную механическую энергию частицы, амплитуду колебаний и амплитуду скорости. Написать зависимости
. Определите для этих трех случаев полную механическую энергию частицы, амплитуду колебаний и амплитуду скорости. Написать зависимости 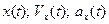 .
.
6. Если  , а
, а 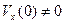 То какая функция удобнее для записи зависимости координаты от времени : синус или косинус?
То какая функция удобнее для записи зависимости координаты от времени : синус или косинус?
7. для случаев а и б из задачи 5 написать зависимость от времени кинетической и потенциальной энергии частицы и изобразить полученные зависимости графически.
ЗАДАЧИ
1. Уравнение колебаний точки имеет вид 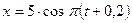 . Определить период колебаний и начальную фазу колебаний.
. Определить период колебаний и начальную фазу колебаний.
2. Написать уравнение гармонического колебания, если начальная фаза равна 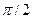 , амплитуда колебаний равна 5 см, а период колебаний равен 8 с.
, амплитуда колебаний равна 5 см, а период колебаний равен 8 с.
3. Некоторая точка движется вдоль оси х по закону 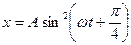 . Найти амплитуду, период колебаний, максимальное значение проекции скорости.
. Найти амплитуду, период колебаний, максимальное значение проекции скорости.
4. Точка совершает колебания вдоль оси х по закону 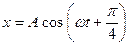 . Построить примерные графики смещения, проекции скорости и проекции ускорения как функции времени.
. Построить примерные графики смещения, проекции скорости и проекции ускорения как функции времени.
5. Некоторая точка движется вдоль оси х по закону 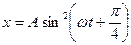 . Найти амплитуду, период колебаний, максимальное значение проекции скорости.
. Найти амплитуду, период колебаний, максимальное значение проекции скорости.
6. Начальная фаза гармонического колебания равна нулю. Через какую долю периода скорость точки будет равна половине ее максимальной скорости?
7. Уравнение колебаний точки массой 1,6 г имеет вид 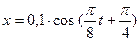 . Построить график зависимости силы, действующей на точку, в пределах одного периода.
. Построить график зависимости силы, действующей на точку, в пределах одного периода.
8. 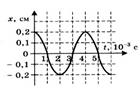 На рисунке представлена зависимость координаты центра шара, подвешенного на пружине, от времени. Определить амплитуду, период и частоту колебаний. Записать уравнение колебаний
На рисунке представлена зависимость координаты центра шара, подвешенного на пружине, от времени. Определить амплитуду, период и частоту колебаний. Записать уравнение колебаний
9. Написать уравнение гармонического колебания, если начальная фаза равна: 1) 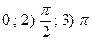 . Амплитуда колебаний
. Амплитуда колебаний 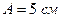 и период колебаний
и период колебаний 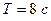 .
.
10. Начертить на одном графике два гармонических колебания с одинаковыми амплитудами 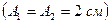 и одинаковыми периодами
и одинаковыми периодами 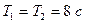 , но имеющими разность фаз:
, но имеющими разность фаз: 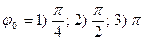 .
.
11. Через сколько времени от начала движения точка, совершающая гармонические колебания, будет иметь смещение от положения равновесия, равное половине амплитуды? Период колебаний равен 24 с, начальная фаза равна нулю.
12. Через сколько времени от начала движения точка, совершающая гармонические колебания по закону 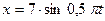 , проходит путь от положения равновесия до максимального смещения?
, проходит путь от положения равновесия до максимального смещения?
13. Уравнение движения точки дано в виде 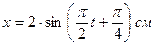 . Найти: 1) период колебаний; 2) максимальную скорость точки; 3) ее максимальное ускорение.
. Найти: 1) период колебаний; 2) максимальную скорость точки; 3) ее максимальное ускорение.
14. Точка совершает гармонические колебания. Период колебаний равен 2 с, амплитуда 50 мм, начальная фаза равна нулю. Найти скорость точки в момент времени, когда смещение точки от положения равновесия равно 25 мм.
15. Уравнение колебаний материальной точки массой 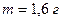 имеет вид
имеет вид 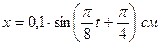 . Построить график зависимости от времени в пределах одного периода силы, действующей на точку. Найти значение максимальной силы.
. Построить график зависимости от времени в пределах одного периода силы, действующей на точку. Найти значение максимальной силы.
16. Максимальная скорость точки, совершающей гармонические колебания, равна 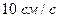 , максимальное ускорение
, максимальное ускорение 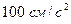 . Найти угловую частоту колебаний, период и амплитуду колебаний. Написать уравнение колебаний, приняв начальную фазу равной нулю.
. Найти угловую частоту колебаний, период и амплитуду колебаний. Написать уравнение колебаний, приняв начальную фазу равной нулю.
17. Частица совершает гармонические колебания вдоль оси х около положения равновесия х=0. Частота колебаний 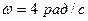 . В некоторый момент времени координата частицы
. В некоторый момент времени координата частицы 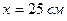 , а ее скорость
, а ее скорость 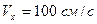 . Найти координату частицы и ее скорость через 2,4 с после этого момента.
. Найти координату частицы и ее скорость через 2,4 с после этого момента.
18. Точка совершает гармонические колебания. Наибольшее смещение точки равно 10 см, наибольшая скорость 20 см/с. Найти угловую частоту колебаний и максимальное ускорение точки.
19. Точка совершает колебания по закону 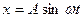 . В некоторый момент времени смещение точки оказалось равным 5 см. Когда фаза колебаний увеличилась вдвое, смещение стало равным 8 см. Найти амплитуду колебаний.
. В некоторый момент времени смещение точки оказалось равным 5 см. Когда фаза колебаний увеличилась вдвое, смещение стало равным 8 см. Найти амплитуду колебаний.
20. Тело совершает гармонические колебания с периодом 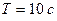 . За какое время тело проходит весь путь от среднего положения до крайнего?
. За какое время тело проходит весь путь от среднего положения до крайнего?
21. При гармонических колебаниях вдоль оси ОХ координата тела меняется по закону 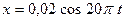 . Чему равна частота колебаний ускорения тела?
. Чему равна частота колебаний ускорения тела?
22. Тело совершает гармонические колебания по закону 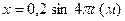 . Период и частота колебаний равны
. Период и частота колебаний равны
23. Определите полную энергию материальной точки массой m, колеблющейся по закону 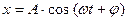 .
.
24. Полная энергия тела, совершающего гармонические колебания равна  , а максимальная сила, действующая на точку- равна 0,5 мН. Напишите уравнение движения точки, если период колебаний равен 4 с, а начальная фаза колебаний
, а максимальная сила, действующая на точку- равна 0,5 мН. Напишите уравнение движения точки, если период колебаний равен 4 с, а начальная фаза колебаний 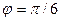 .
.
25. Материальная точка массой 50 г совершает колебания, уравнение которых имеет вид 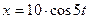 . Найти силу, действующую на точку в момент, когда фаза
. Найти силу, действующую на точку в момент, когда фаза 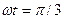 .
.
26. Колебания материальной точки массой 0,1 кг происходят согласно уравнению 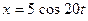 . Определите максимальное значение возвращающей силы и максимальное значение кинетической энергии.
. Определите максимальное значение возвращающей силы и максимальное значение кинетической энергии.
Семинар 12
