Примеры решения задач. Пример 1. Точечный заряд q находится на плоской границе двух диэлектрических полупространств - с проницаемостями e1 и e2
Пример 1. Точечный заряд q находится на плоской границе двух диэлектрических полупространств - с проницаемостями e1 и e2. Найти величину векторов 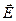 и
и 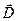 .
.
Пусть j1 – потенциал электрического поля в первом диэлектрике, j2 – во втором. Потенциалы j1 и j2 удовлетворяют уравнению Лапласа:
Dj1 = 0 и Dj2 = 0.
 В силу сферической симметрии задачи потенциалы j1 и j2 являются функциями только расстояния r от заряда q. Тогда в сферической системе координат
В силу сферической симметрии задачи потенциалы j1 и j2 являются функциями только расстояния r от заряда q. Тогда в сферической системе координат
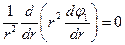 и
и 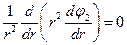 .
.
Решения этих уравнений имеют вид:
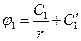 и
и 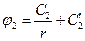 .
.
Принимая потенциал бесконечно удаленной точки равным нулю, получаем 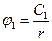 и
и 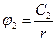 .
.
Эти результаты справедливы для любого направления вектора  , в том числе и вдоль границы раздела диэлектриков. Следовательно, условие непрерывности потенциалов на границе приводит к равенству:
, в том числе и вдоль границы раздела диэлектриков. Следовательно, условие непрерывности потенциалов на границе приводит к равенству:
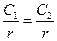 и
и 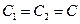 .
.
Таким образом, 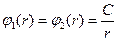 . Соответственно,
. Соответственно, 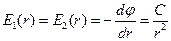 .
.
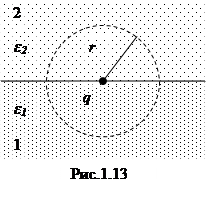
Для нахождения постоянной С воспользуемся теоремой Гаусса – рассмотрим поток вектора электрической индукции 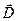 через поверхность сферы произвольного радиуса r с центром в точке расположения заряда (см. рис.1.13):
через поверхность сферы произвольного радиуса r с центром в точке расположения заряда (см. рис.1.13):
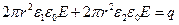 .
.
Подставляя 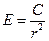 , получаем
, получаем
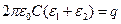 и
и 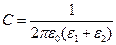 .
.
Тогда
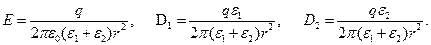
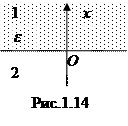 Пример 2.Бесконечное однородное полупространство с диэлектрической проницаемостью e граничит с вакуумом, как показано на рис 1.14. Диэлектрик заряжен с объемной плотностью заряда
Пример 2.Бесконечное однородное полупространство с диэлектрической проницаемостью e граничит с вакуумом, как показано на рис 1.14. Диэлектрик заряжен с объемной плотностью заряда 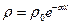 . Определить потенциал и напряженность электрического поля в вакууме и в диэлектрике.
. Определить потенциал и напряженность электрического поля в вакууме и в диэлектрике.
Потенциал j1 поля в диэлектрике подчиняется уравнению Пуассона 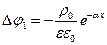 , а потенциал j2 – уравнению Лапласа
, а потенциал j2 – уравнению Лапласа 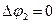 .
.
Из геометрии задачи видно, что потенциалы обеих областей зависят только от координаты х и, следовательно, оператор Лапласа 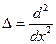 . Тогда
. Тогда 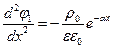 и
и 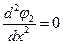 .
.
Выполняя интегрирование, получаем: 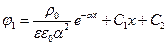 и
и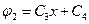 .
.
Примем 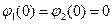 . Тогда С4 = 0, С2 =
. Тогда С4 = 0, С2 = 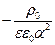 и
и
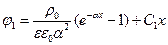 ,
, 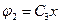 .
.
Т.к.  , то
, то 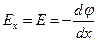 и
и 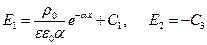 .
.
Из условия непрерывности нормальных составляющих вектора электрической индукции на границе х = 0 следует, что 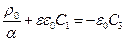 .
.
Дополнительным условием для нахождения постоянных С1 и С2 может служить физически обоснованное требование обращения в нуль напряженности электрического поля при х ® ¥. Тогда С1 = 0 и 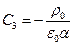 . Окончательно получаем
. Окончательно получаем
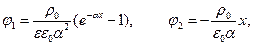
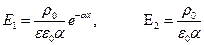 .
.
Таким образом, напряженность электрического поля в диэлектрике экспоненциально убывает с увеличением х, а поле в вакууме однородно.
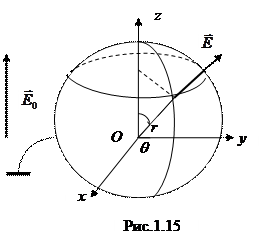
Пример 3. Проводящая заземленная сфера радиуса R помещена в однородное электрическое поле напряженностью Е0. Определить распределение плотности заряда, индуцированного на поверхности сферы.
При помещении проводящей сферы в однородное электрическое поле на «полюсах« ее поверхности индуцируются заряды противоположного знака, приводящие к искажению силовых линий поля, как показано на рис.1.7 к примеру 1 п.1.3.1.
Введем систему координат так, чтобы ось Оz декартовой системы координат совпадала с направлением вектора  (рис.1.15). В силу осевой симметрии распределения поверхностных зарядов потенциал электрического поля зависит только от расстояния от центра сферы r и от азимутального угла q, т.е.
(рис.1.15). В силу осевой симметрии распределения поверхностных зарядов потенциал электрического поля зависит только от расстояния от центра сферы r и от азимутального угла q, т.е. 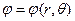 . При этом потенциал внутри и на поверхности сферы равен нулю, а вне сферы удовлетворяет уравнению Лапласа
. При этом потенциал внутри и на поверхности сферы равен нулю, а вне сферы удовлетворяет уравнению Лапласа
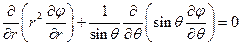 .
.
Подстановка решения в форме 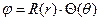 позволяет разделить переменные и записать два уравнения для функций R(r), Q(q):
позволяет разделить переменные и записать два уравнения для функций R(r), Q(q):
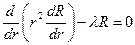 ,
,
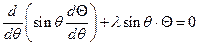 ,
,
где l - положительная постоянная величина.
Решением второго из уравнений при 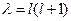 и l = 0, 1, 2,… являются полиномы Лежандра
и l = 0, 1, 2,… являются полиномы Лежандра 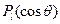 :
:
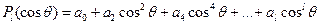 - для четных l и
- для четных l и
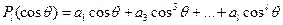 - для нечетных l.
- для нечетных l.
Подставляя значения l в уравнение для функции R(r), получаем уравнение Эйлера
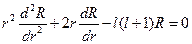 ,
,
которое приводится к дифференциальному уравнению второго порядка с постоянными коэффициентами заменой переменной 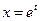 :
:
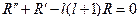 .
.
Решения уравнения имеют вид: 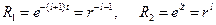 . Таким образом, общим решением уравнения Лапласа является функция
. Таким образом, общим решением уравнения Лапласа является функция
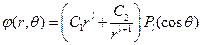 .
.
Постоянные интегрирования С1 и С2, а также степень полинома l найдем из граничных условий – равенства потенциала нулю на поверхности сферы r = R и отсутствию искажения внешнего поля на бесконечности. Радиальная составляющая напряженности электрического поля
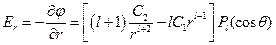 .
.
При r ® ¥ с одной стороны 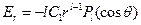 , а с другой -
, а с другой - 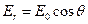 . Следовательно,
. Следовательно, 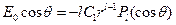 .
.
Сравнивая коэффициенты при одинаковых степенях cosq в левой и правой частях этого равенства, приходим к выводу, что l = 1. Таким образом,
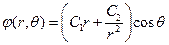 ,
, 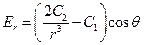
Теперь 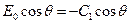 , т.е.
, т.е. 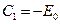 . Из условия равенства нулю потенциала на поверхности сферы получаем:
. Из условия равенства нулю потенциала на поверхности сферы получаем: 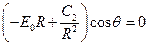 , т.е.
, т.е. 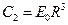 .
.
Окончательно получаем 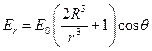 . Тогда на поверхности сферы
. Тогда на поверхности сферы 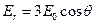 .
.
С другой стороны, вблизи поверхности сферы 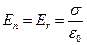 . Следовательно,
. Следовательно, 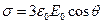 .
.
