Запишите решение заданий уровня С с полным обоснованием
С1.К графику функции f (х)=х 
-4х проведена касательная в точке М(1;-3). Найдите абсциссу точки пересечения касательной с осью Ох.
С2.Число 18 представьте в виде двух положительных слагаемых таких, что сумма их квадратов принимает наименьшее значение.
Диагностическая контрольная работа
По алгебре и началам анализа
«Производная функции. Приложения производной»
Вариант 2
Запишите вариант правильного ответа заданий уровня А
А1.Найдите производную функции f(x)=sin x-cos x.
| а) cos x-sin x | б) cos x+sinx | в) -cos x-sin x | г) sin x-cos x |
А2.Найдите производную функции y=(-2x+3)8
| а) -16(-2x+3)7 | б) -24(-2x+3)7 | в) 8(-2x+3)7 | г) -8(-2x+3)7 |
А3.Укажите функцию, являющуюся первообразной для функции f(x)=x2-10x.
а) 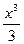 -5x2 | б) x3-10x2 | в) 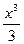-10x2 | г) 2x-10 |
А4.Найдите значение 
(2), если f(x)=lnx- 
.
а) 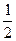 -ln2 | б) 0 | в) - 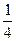 | г)  |
А5. Найдите производную функции g(x)=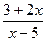 
.
а) - 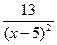 | б) 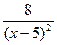 | в) 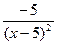 | г)  |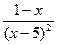
А6.Найдите производную функции y=3x2cos x.
| а) -6xsin x | б) 6xcos x-3x2sin x | в) x3cos x+3x2sin x | г) 6xcos x+3x2sin x |
А7.Найдите угловой коэффициент касательной к графику функции
f(x)=x3-3x2-11 в точке с абсциссой x0=2.
| а) 0 | б) -11 | в) -15 | г) -26 |
А8.Найдите тангенс угла наклона касательной к графику функции y=3lnx в точке с абсциссой равной 3.
| а) 3ln3 | б) 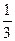 | в) 1 | г) 3 |
А9.Значение функции y= 
- 
-3x-2 в точке минимума равняется
а) -  | б) - 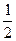| в) -2 | г) 3 |
А10.Сколько экстремумов имеет функция у=- 
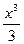- +5х -1?
| а) 2 | б) 3 | в) 1 | г) 4 |
А11.Найдите площадь фигуры, ограниченной графиком функции у=х -4х+5, прямыми х=1, х=4 и осью абсцисс.
а) 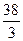 | б) 6 | в) 18 | г) 48 |
А12.Найдите наибольшее значение функции у=2cosх-14.
| а) -16 | б) 2 | в) -14 | г) -12 |