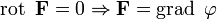Векторный и скалярный потенциалы. Градиентные (калибровочные) преобразования. Лоренцевская и кулоновская калибровки потенциалов

Рассмотрим систему уравнений Максвелла , например - в системе единиц Гаусса в частности уравнение b) - закон отсутствия магнитных зарядов -

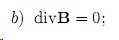
вектор индукции магнитного поля B из этого уравнения можно представить в виде:

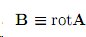
где A -вектор, получивший название векторного потенциала.

Приведённое выше равенство является определением векторного потенциала.

С учетом данного определенияуравнение с) - Закон электромагнитной индукции Фарадея -

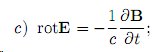
можно переписать в виде:

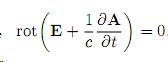
Из данного равенства вытекает, что =

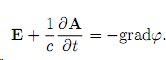
Здесь ϕ - скалярная функция, называемая скалярным потенциалом. Знак минус в уравнении выше выбран в соответствии
с историческими определениями.

Последнее равенство соответствует следующим свойствам ротора :

· Если поле F потенциально, его ротор равен нулю (поле F — безвихревое)=

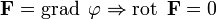
· Верно и обратное: если поле безвихревое, то оно потенциально:=