Основной особенностью периодических функций является повторяемость их числовых значений через равные промежутки изменения значений аргумента

Для активизации мыслительной деятельности учащихся при изучении теоретического материала рекомендуется предлагать учащимся проблемные вопросы.

1. Может ли периодическая функция: а) быть возрастающей во всей области определения; б) иметь только два промежутка монотонности? (Нет)

2. Может ли периодическая функция иметь только один период? (Нет)

3. Приведите примеры периодических процессов в естествознании, физике и соответствующих им функций.

4. Верны ли утверждения: а) Если график функции f имеет две оси симметрии х = а и х = b (a < b), то f – периодическая (Да). б) Если функция f – периодическая, то g(x) = 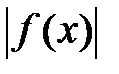- периодическая функция (Да). в) Если функция f – периодическая, то 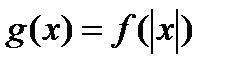- периодическая функция? (Нет, например, 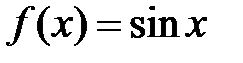- периодическая, а 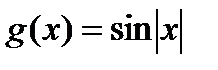- непериодическая.)

5. Приведите пример периодической функции, являющейся суммой (разностью) двух непериодических функций. (Например, 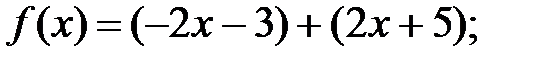f(x) =2 – периодическая функция.)

Для дальнейшего разъяснения и закрепления изученного материала рекомендуются разнообразные упражнения. Их подбор для конкретного класса зависит от целей обучения, математических способностей и интереса учащихся к математике.

Приведем примеры упражнений.

1. Вычислите: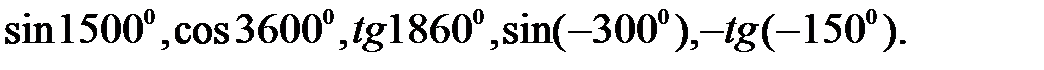

2. Является ли периодической функция: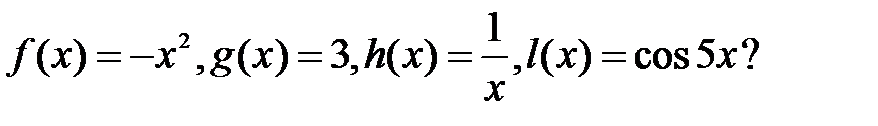

3. Найдите период функции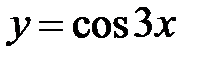

Решение. Пусть Т – период данной функции. Тогда 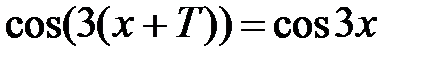для любого х Î R. Пусть х=0, тогда 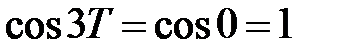. На промежутке [0;2π] уравнение 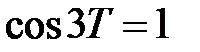имеет два решения: 3Т=0 и 3Т=2. По условию Т ¹ 0, поэтому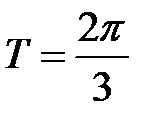

Примечание. Период функции можно найти, пользуясь свойством 4.

4. Найдите наименьший положительный период функции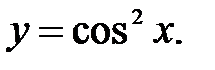

Решение: 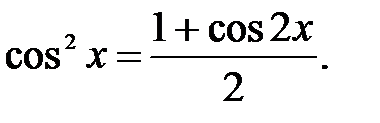Период функции 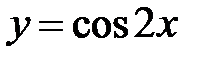равен π (см. свойство 4), значит, и периодом функции 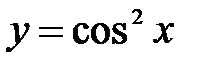является число π. (см. свойство 5).

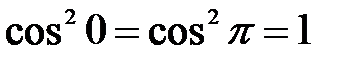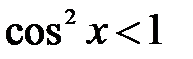Так как и для любого x Î (0;π), то число π является наименьшим периодом данной функции.

5. Найдите период функции .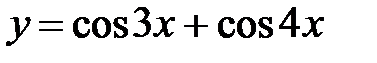

Решение. Функция 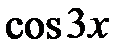имеет период 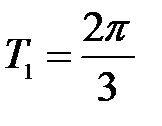,а функция 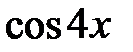- период 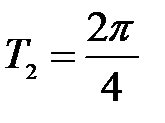. Периоды Т₁ и Т₂ соизмеримы: 3 Т₁ = 4Т₂ = 2π. Следовательно, 2π является периодом данной функции.

6. Докажите, что следующие функции не являются периодическими:

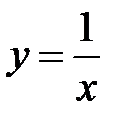
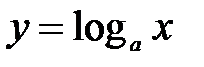
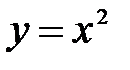
7. Докажите, что функция 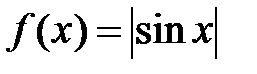является периодической с периодом π.

Решение. D(f) = R. Для любого х точки х+π и х-π принадлежат области определения:

f(x+π) = |sin(x+π)| = |-sinx| = |sinx| = f(x).

8. Постройте график такой периодической функции с периодом Т =1, которая на промежутке [0;1) задана формулой:

а) 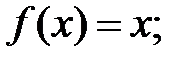б) .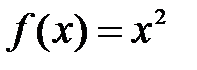

В заключение отметим, что в результате изучения периодичности функций учащиеся должны знать определение периодических функций, наименьшие положительные периоды тригонометрических функций, иметь представление о графике периодической функции, уметь применятьсвойство периодичности тригонометрических функций, иметь представление о графике периодической функции, уметь применять свойство периодичности тригонометрических функций при вычислении их значений.

График функции

Понятие "график функции" известно учащимся из курса алгебры: "Графиком функции называется множество всех точек, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции".

Способ построения графика функции "по точкам" не является совершенным. В курсе алгебры и начал анализа рассматривается применение производной к исследованию функций и построению их графиков.

Пусть нужно построить график функции 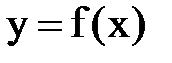. При исследовании функции f(x) и построении ее графика полезно придерживаться следующего плана:

1. Найти область определения функции.

2. Выяснить, является ли функция f(x) четной или нечетной, периодической.

3. Найти точки пересечения графика функции f(x) с осями координат.

4. Определить промежутки возрастания и убывания.

5. Найти точки экстремума и значения функции f(x) в этих точках.

Исследование функций на возрастание (убывание) и на экстремум удобно проводить с помощью производной. Для этого сначала находят производную функции f(x) и её критические точки, а затем выясняют, какие из них являются точками экстремума.

Следует иметь в виду, что при построении графика функции не всегда нужно точно следовать указанному плану. Например, не всегда учащиеся смогут найти точки пересечения графика функции с осью OX, даже если они существуют. Иногда дополнительно находят координаты некоторых точек графика.

Пример. Исследуем функцию f(x) = 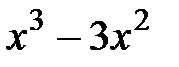и построим ее график.

Решение.

1. D(f)=R, так как f(x) – многочлен. Функция непрерывна и дифференцируема на D(f).

2. f(-x) = (-x)³ – 3*(-x)² = -x³ – 3x²;

-f(x) = -x³ + 3x².

Так как f(-x) 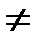f(x) и f(x) 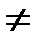-f(x), то функция не является четной и не является не четной.

3. Находим точки пересечения графика функции f(x) с осями координат: x = 0, y = 0;

y = 0, x³-3x² = 0; x²(x-3) = 0, x = 0 или x = 3.

(0;0), (3;0) – точки пересечения с осями.

4. Найдем критические точки функции f(x):

f’(x) = 3x²-6x = 3x(x-2), f’(x) = 0,

3x(x-2) = 0, x = 0 или x = 2.

5. Составим таблицу.

x	(- 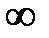; 0)		(0 ; 2)		(2 ; + )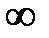
f’(x)	+		-		+
f(x)		0 max		-4 min

6. Дополнительные точки. Если х = -1, то f(-1) = 4.

7. Строим график.

Примеры упражнений. Исследуйте с помощью производной функции и постройте их графики:

а) f(x) = 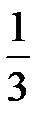x³+x²-3x; б) f(x) = ;

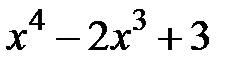в) f(x) = 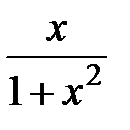; г) f(x) = x + ;

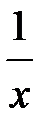д) f(x) = 1-2sinx; д) f(x) = 1+2cos .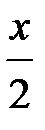

В некоторых случаях график функции можно построить по заданной его части или по графику данной функции с помощью геометрических преобразований: параллельного переноса, растяжения (или сжатия), преобразования симметрии. Для выработки у учащихся умения строить графики функций таким способом используются упражнения. Например, как, зная график функции y = sinx, построить график каждой из функций:

a) y = -sinx ; б) y = sinx- 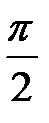; в) y = sinx +1,5 ;

г) y = 2sinx ; д) y = 0.5sinx ; е) y = sin(x- ) ;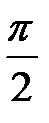

ж) y = sin(x+ 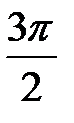) ; з) y = -2sin(x- ) .

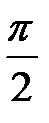В некоторых случаях для построения графика необходимо произвести тождественное преобразование выражения, задающего функцию, с целью приведения его к виду, позволяющему определить вид графика и построить его. Приведем примеры упражнений.

Построить графики функций:

а) y = 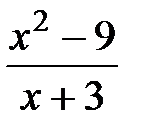; б) y = ;

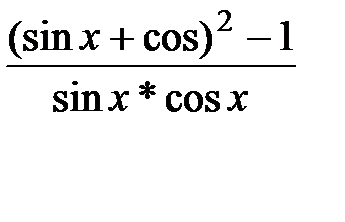в) y = 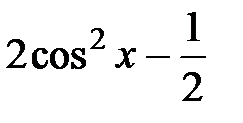; г) y = .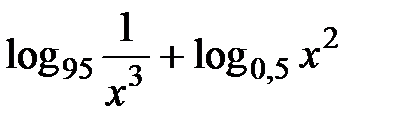

В процессе изучения курса «АиНА» рекомендуется достичь прочных навыков чтения графиков функций. В связи с этим необходимо сформировать следующие умения:

1.

X2

X7

X1

X6

X5

X4

X3

Выявлять «характерные» точки графика (рис.), абсциссы этих точек обозначены x₁, x₂, … ,x₇ ;

2. Находить область определения функции, область изменения функции, определять промежутки монотонности по графику;

3. Определять знак производной не промежутках возрастания и убывания функции;

4. Находить точки максимумов и минимумов; пояснять, что в этих точках производная обращается в нуль;

5. Указывать наибольшее и наименьшее значение функции.