Пример построения эпюр ВСФ
Раздел 7.
Сложное сопротивление бруса
До сих пор изучались простые виды деформации бруса: 1) центральное осевое растяжение (сжатие); 2) чистый сдвиг; 3) плоский изгиб, когда 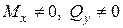 ; 4) кручение. Каждый вид этих деформаций вызывается своей нагрузкой.
; 4) кручение. Каждый вид этих деформаций вызывается своей нагрузкой.
На практике часто на конструкцию действует достаточно произвольная нагрузка, которая может вызвать несколько простых деформаций одновременно. В этом случае стержень (брус) будет испытывать сложную деформацию.
Определение внутренних силовых факторов (ВСФ)
При сложной деформации в поперечном сечении бруса могут возникнуть шесть компонент внутренних сил и моментов (ось 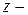 всегда вдоль оси бруса, оси
всегда вдоль оси бруса, оси 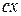 и
и 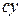 – в поперечном сечении бруса и составляют правую систему координат
– в поперечном сечении бруса и составляют правую систему координат 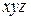 ):
): 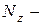 продольная сила,
продольная сила, 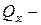 поперечная (перезывающая) сила вдоль оси
поперечная (перезывающая) сила вдоль оси 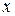 ,
, 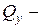 поперечная сила вдоль оси
поперечная сила вдоль оси 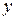 ,
, 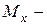 изгибающий момент относительно (вокруг) оси
изгибающий момент относительно (вокруг) оси 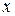 ,
, 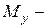 изгибающий момент относительно оси
изгибающий момент относительно оси 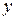 ,
, 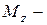 крутящий (относительно оси
крутящий (относительно оси 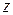 ) момент. Для их определения в произвольном сечении бруса используют «метод сечений», который дает полученные ранее (1.5) шесть уравнений, рассматривая одну из отсеченных частей бруса (левую или правую):
) момент. Для их определения в произвольном сечении бруса используют «метод сечений», который дает полученные ранее (1.5) шесть уравнений, рассматривая одну из отсеченных частей бруса (левую или правую):
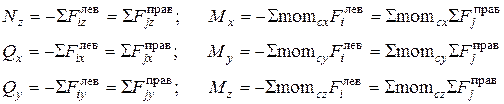 (7.1)
(7.1)
На рис. 7.1 показаны положительные направления всех ВСФ в сечении левой части бруса.
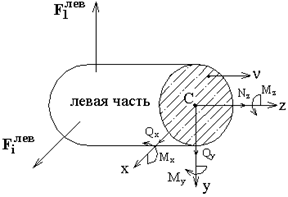 Рис.7.1 Рис.7.1 | Левой отсеченной частьюусловно будем считать ту часть бру-са, у которой нормаль 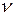 к сечению (внешняя) направлена вдоль оси к сечению (внешняя) направлена вдоль оси 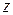 (у правой части нормаль (у правой части нормаль 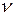 направлена против оси направлена против оси 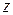 ). В сечении левой части: ). В сечении левой части: 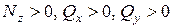 направлены вдоль осей направлены вдоль осей 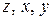 соответственно; соответственно; 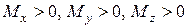 , если с , если с |
концов осей 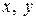 и
и 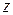 эти моменты видны против хода часовой стрелки или от этих моментов правый винт (буравчик) перемещается вдоль направлений осей
эти моменты видны против хода часовой стрелки или от этих моментов правый винт (буравчик) перемещается вдоль направлений осей 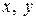 и
и 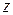 соответственно.
соответственно.
В сечении правой части бруса, отброшенной на рис. 7.1, положительные направления ВСФ по III закону Ньютона (действия и противодействия) направлены противоположно показанным на рис. 7.1 направлениям. Составляющие (компоненты) по осям внешних сил 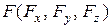 для левой и правой частей в уравнениях (7.1) положительны, если они направлены вдоль осей; внешние моменты от них в сечении бруса относительно осей
для левой и правой частей в уравнениях (7.1) положительны, если они направлены вдоль осей; внешние моменты от них в сечении бруса относительно осей 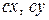 и
и 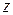 положительны, если от них правый винт (буравчик) перемещается вдоль направлений осей
положительны, если от них правый винт (буравчик) перемещается вдоль направлений осей 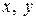 и
и 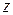 (совпадают с направлениями
(совпадают с направлениями 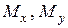 и
и 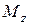 на рис. 7.1).
на рис. 7.1).
С учетом этих правил по формулам (7.1) можно построить эпюры (графики) всех ВСФ по длине бруса, по которым определяется опасное сечение бруса.
При построении эпюр по формулам (7.1):
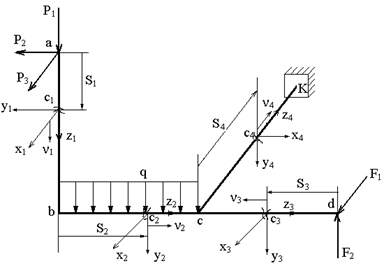 |
Рис.7.2
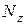 строится в любой плоскости (
строится в любой плоскости ( 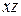 или
или 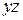 ), обязательно указать знак; Эп.
), обязательно указать знак; Эп. 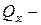 в плоскости
в плоскости 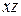 , положительные значения откладывать вдоль направления оси
, положительные значения откладывать вдоль направления оси 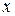 ; Эп.
; Эп. 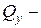 в плоскости
в плоскости 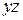 ,
, 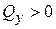 вдоль оси
вдоль оси 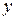 ; Эп.
; Эп. 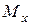 строится в плос-кости изгиба бруса
строится в плос-кости изгиба бруса 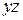 ,
, 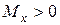 вдоль оси
вдоль оси 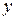 ;
;
Эп. 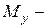 в плоскости
в плоскости 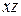 ,
, 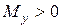 вдоль направления оси
вдоль направления оси 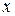 ;
;
Эп. 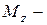 в любой плоскости (
в любой плоскости ( 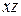 или
или 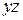 ), желательно указывать знак.
), желательно указывать знак.
Часто ось бруса состоит из отрезков прямых, соединенных под углами 90°(ломанный брус) и загружена произвольной нагрузкой. В этом случае брус разбивается на участки, границами которых служат точки излома оси бруса, точки приложения сосредоточенных нагрузок, начало и конец распределенных нагрузок. На каждом участке вводим правую систему координат 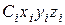 (т.
(т. 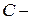 центр тяжести поперечного сечения бруса, оси
центр тяжести поперечного сечения бруса, оси 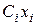 и
и 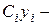 главные центральные оси сечения; оси правые, если кратчайший поворот оси
главные центральные оси сечения; оси правые, если кратчайший поворот оси 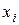 к оси
к оси 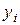 с конца оси
с конца оси 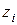 виден против хода часовой стрелки).
виден против хода часовой стрелки).
Пример построения эпюр ВСФ
Рассмотрим «ломанный брус», показанный на рис. 7.2.
Исходные данные:
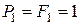 кН,
кН, 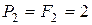 кН,
кН, 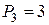 кН,
кН, 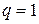 кН/м,
кН/м, 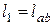 ,
, 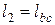 ,
, 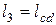 ,
, 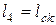 ,
, 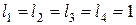 м
м
Из рис. 7.2 видно, что брус имеет четыре участка. За первый участок примем тот, который имеет свободный конец ( 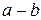 или
или 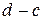 ). Выберем участок
). Выберем участок 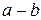 длиной
длиной 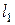 . Ось
. Ось 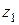 вдоль оси бруса от т. а. На этом участке возьмем произвольное сечение с ц.т.
вдоль оси бруса от т. а. На этом участке возьмем произвольное сечение с ц.т. 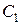 на расстоянии
на расстоянии 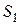 от т.а и проведем оси
от т.а и проведем оси 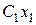 и
и 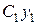 так, чтобы с осью
так, чтобы с осью 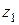 они составили правую систему координат
они составили правую систему координат 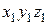 . Для записи уравнений (7.1) выгоднее рассмотреть часть бруса
. Для записи уравнений (7.1) выгоднее рассмотреть часть бруса 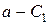 с известными нагрузками
с известными нагрузками 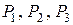 . Внешняя нормаль
. Внешняя нормаль 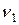 к сечению этой части направлена вдоль оси
к сечению этой части направлена вдоль оси 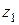 , поэтому эта часть считается «левой» при использовании формул (7.1). Правую часть рассматривать невыгодно, т.к. она более сложная и содержит в заделке «k» шесть опорных реакций (которые предварительно придется найти). Далее оси
, поэтому эта часть считается «левой» при использовании формул (7.1). Правую часть рассматривать невыгодно, т.к. она более сложная и содержит в заделке «k» шесть опорных реакций (которые предварительно придется найти). Далее оси 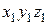 поступательно, без вращения вокруг оси
поступательно, без вращения вокруг оси 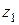 (поворачиваются вокруг оси х), перемещаются на второй участок
(поворачиваются вокруг оси х), перемещаются на второй участок 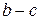 и в сечении
и в сечении 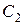 оси
оси 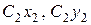 и ось
и ось 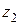 . Проще рассмотреть участки
. Проще рассмотреть участки 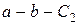 и эта часть бруса считается тоже левой, т.к. нормаль
и эта часть бруса считается тоже левой, т.к. нормаль 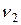 в сечении
в сечении 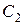 направлена вдоль оси
направлена вдоль оси 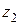 . Положение сечения
. Положение сечения 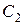 определим расстоянием
определим расстоянием 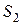 , причем
, причем 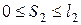 . Далее оси перемещаем на III участок
. Далее оси перемещаем на III участок 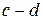 и в сечении
и в сечении 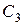 проводим оси
проводим оси 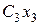 и
и 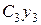 . Положение сечения
. Положение сечения 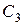 определим расстоянием
определим расстоянием 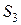 (
( 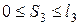 ) и рассмотрим правую часть
) и рассмотрим правую часть 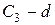 , т.к. нормаль
, т.к. нормаль 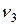 в сечении направлена против оси
в сечении направлена против оси 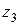 . На IV участок оси переводим из положения
. На IV участок оси переводим из положения 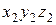 поворачивая их в т. С вокруг оси
поворачивая их в т. С вокруг оси 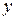 , ось
, ось 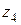 вдоль стержня
вдоль стержня 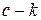 . Проводим произвольно сечение в т.
. Проводим произвольно сечение в т. 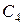 , в котором располагаем оси
, в котором располагаем оси 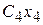 и
и 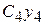 . Рассмотрим всю переднюю часть, поэтому сечение
. Рассмотрим всю переднюю часть, поэтому сечение 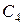 определим расстоянием
определим расстоянием 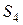 (
( 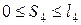 ), эта часть бруса будет «левой», т.к.
), эта часть бруса будет «левой», т.к. 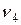 направлена вдоль оси
направлена вдоль оси 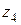 (для правой части надо определить 6 опорных реакций в заделке «k»).
(для правой части надо определить 6 опорных реакций в заделке «k»).
Для каждого участка бруса запишем формулы (7.1), по которым построим все эпюры ВСФ:
I участок 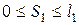 (левая часть)
(левая часть)
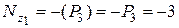 кН
кН 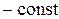
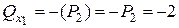 кН
кН 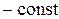
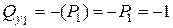 кН
кН 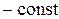
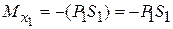 – линейная зависимость:
– линейная зависимость:
Считаем : 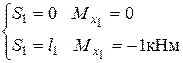
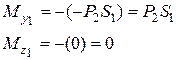 Считаем
Считаем 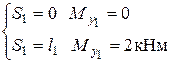
По этим данным строим эпюры (графики) всех ВСФ на I участке на рис.7.3 по вышеуказанным правилам.
II участок 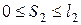 (левая часть)
(левая часть)
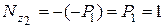 кН
кН 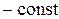
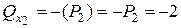 кН
кН
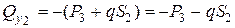 – линейная зависимость
– линейная зависимость
Считаем : 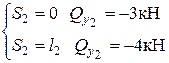
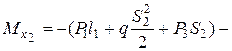 квадратная парабола
квадратная парабола
Считаем 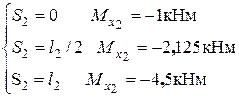
Считаем
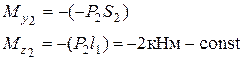
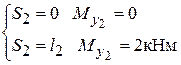
Строим эпюры на II участке
III участок 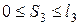 (правая часть)
(правая часть)
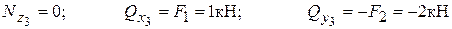
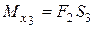 Считаем
Считаем 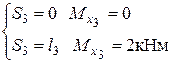
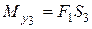 Считаем
Считаем 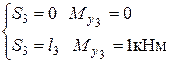
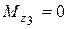 .
.
Строим эпюры на III участке.
IV участок 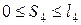 (левая часть)
(левая часть)
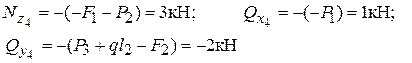
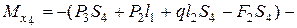 линейная зависимость
линейная зависимость
Считаем 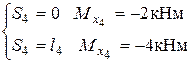
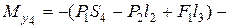 линейная зависимость
линейная зависимость
Считаем 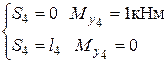
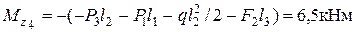
Эпюры всех внутренних силовых факторов приведены на рис. 7.3 (1÷6).
По эпюрам можно определить тип сложного сопротивления бруса, найти опасное (расчетное) сечение на каждом участке «ломанного» бруса и величины всех ВСФ в них.
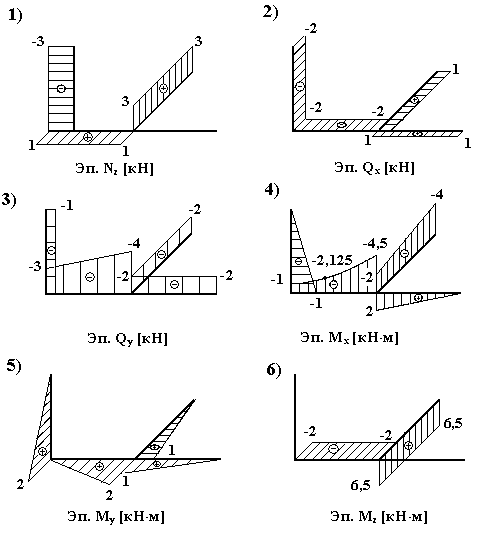
Рис.7.3
Типы сложного сопротивления бруса:
Косой изгиб: обязательно 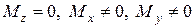 .
.
Изгиб с кручением: обязательно 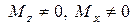 или
или 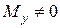 или оба
или оба 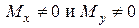 .
.
Внецентренное растяжение (сжатие): обязательно 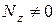 ,
, 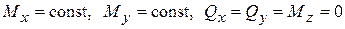 .
.
Другие комбинации ВСФ относятся к общему случаю сложного сопротивления бруса.
Определим тип сложного сопротивления, найдем опасное (расчетное) сечение на каждом участке бруса из анализа полученных эпюр рис. 7.3.
I участок: Здесь косой изгиб и сжатие. Опасное сечение при 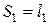 , где:
, где: 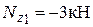 ,
, 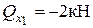 ,
, 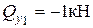 ,
, 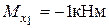 ,
, 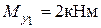 ,
, 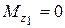 .
.
II участок: Здесь косой изгиб с кручением и растяжением. Опасное сечение при 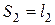 , где:
, где: 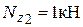 ,
, 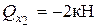 ,
, 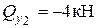 ,
, 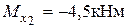 ,
, 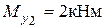 ,
, 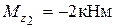 .
.
III участок: Здесь косой изгиб. Опасное сечение 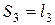 , где:
, где: 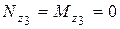 ,
, 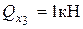 ,
, 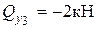 ,
, 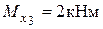 ,
, 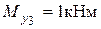 .
.
IV участок: Здесь косой изгиб с кручением и растяжением. Опасное сечение при 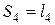 , где:
, где: 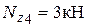 ,
, 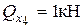 ,
, 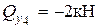 ,
, 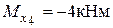 ,
, 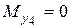 ,
, 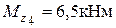 .
.
Т.к. в опасном сечении 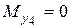 , то расчет этого сечения можно вести по формулам плоского изгиба.
, то расчет этого сечения можно вести по формулам плоского изгиба.
Определение напряжений
Ранее получены формулы для определения 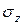 от
от 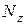 и
и 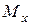 :
: 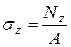 ,
, 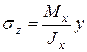 . По аналогии можно записать формулу для
. По аналогии можно записать формулу для 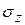 от
от 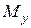
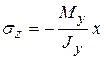 (а). В этих формулах х и у координаты точки сечения бруса, где определяется
(а). В этих формулах х и у координаты точки сечения бруса, где определяется 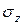 . Очевидно, что при
. Очевидно, что при 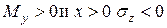 (сжатие) получается. Поэтому в формуле (а) стоит знак минус. При одновременном действие в сечении бруса
(сжатие) получается. Поэтому в формуле (а) стоит знак минус. При одновременном действие в сечении бруса 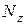 ,
, 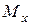 и
и 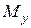 суммарные напряжения в любой точки сечения с координатами х и у можно определить так
суммарные напряжения в любой точки сечения с координатами х и у можно определить так
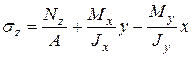 (7.2)
(7.2)
Это одна из основных формул сопротивления материалов. В (7.2) 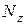 ,
, 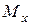 ,
, 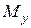 и координаты точки сечения х и у надо подставлять со своими знаками. Если
и координаты точки сечения х и у надо подставлять со своими знаками. Если 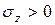 получится, значит в этой точке сечения – растяжение, если
получится, значит в этой точке сечения – растяжение, если 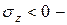 то сжатие. Это важно при оценке прочности хрупких материалов.
то сжатие. Это важно при оценке прочности хрупких материалов.
От 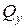 в сечении бруса возникают
в сечении бруса возникают 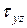 , определяемые по известной формуле Журавского
, определяемые по известной формуле Журавского 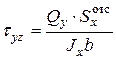 . Аналогично, от
. Аналогично, от 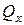 возникают
возникают 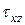 , определяемые по формуле
, определяемые по формуле 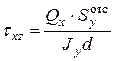 . От кручения
. От кручения 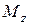 круглых валов возникают
круглых валов возникают 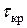 , определяемые известной формулой
, определяемые известной формулой 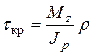 . Направления касательных напряжений от
. Направления касательных напряжений от 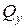 ,
, 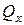 и
и 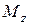 были выяснены раньше. В каждой точки сечения эти напряжения надо суммировать геометрически (векторно), т.е. суммарные напряжения
были выяснены раньше. В каждой точки сечения эти напряжения надо суммировать геометрически (векторно), т.е. суммарные напряжения
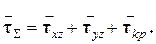
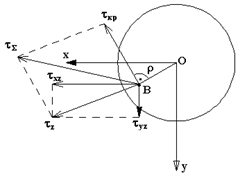 |
Рис.7.4
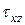 ,
, 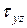 и
и 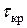 в т.В круглого сечения бруса. Определив в этой же точке «В»
в т.В круглого сечения бруса. Определив в этой же точке «В» 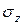 от
от 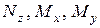 по (7.2), можно оценить прочность в точке «В» сечения по одной из теорий прочности. Например, по III теории прочности получим
по (7.2), можно оценить прочность в точке «В» сечения по одной из теорий прочности. Например, по III теории прочности получим 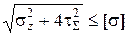
Рассмотрим подробнее частные случаи сложного сопротивления бруса.
I. КОСОЙ ИЗГИБ
Здесь в поперечных сечениях бруса могут быть 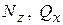 ,
, 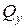 ,
, 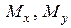 , а
, а 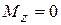 . Косой изгиб может быть чистым, когда вдоль бруса отсутствуют
. Косой изгиб может быть чистым, когда вдоль бруса отсутствуют 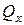 =
= 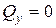 и поперечным, когда
и поперечным, когда 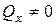 и
и 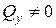 , а
, а 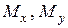 переменны по длине бруса. Косой изгиб может быть плоским, когда вся внешняя нагрузка лежит в одной плоскости и не плоским, когда нагрузки в плоскостях
переменны по длине бруса. Косой изгиб может быть плоским, когда вся внешняя нагрузка лежит в одной плоскости и не плоским, когда нагрузки в плоскостях 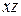 и
и 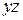 изменяются произвольно по длине бруса.
изменяются произвольно по длине бруса.
Величины и знаки 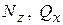 ,
, 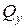 ,
, 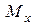 и
и 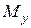 в любом сечении бруса определяются из эпюр. Введем понятие полный изгибающий момент, определяемый так
в любом сечении бруса определяются из эпюр. Введем понятие полный изгибающий момент, определяемый так
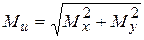 (7.3)
(7.3)
Если 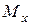 и
и 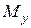 представить в виде векторов (длина векторов определяет величину
представить в виде векторов (длина векторов определяет величину 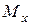 и
и 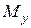 , а направления по правилу правого «буравчика»), то
, а направления по правилу правого «буравчика»), то 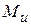 есть геометрическая сумма
есть геометрическая сумма 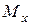 и
и 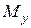 , что показано на рис. 7.5. Положение
, что показано на рис. 7.5. Положение 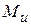 удобно определять углом
удобно определять углом 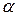 , который он составляет с осью
, который он составляет с осью 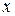 (
( 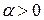 отсчитывается от оси
отсчитывается от оси 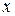 против хода часовой стрелки). Из рис. 7.5 видно:
против хода часовой стрелки). Из рис. 7.5 видно:
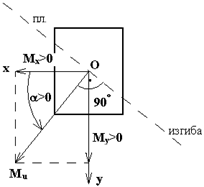 Рис.7.5 Рис.7.5 | 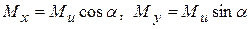 (1) Отсюда (1) Отсюда 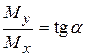 (2) Нормальное напряжение (2) Нормальное напряжение 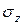 в любой точки сечения с координатами в любой точки сечения с координатами 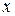 и и 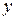 определяется по формуле (7.2), полагая в ней определяется по формуле (7.2), полагая в ней 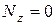 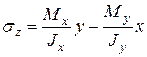 (7.4) (7.4) |
С учетом (1) 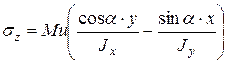 (7.5)
(7.5)
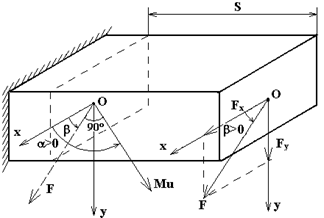 Рис.7.6 Рис.7.6 | В формулы (7.4) и (7.5) все надо подставить со своими знаками: знаки 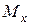 и и 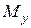 берутся из эпюр, берутся из эпюр, 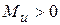 всегда. Величина и знак всегда. Величина и знак 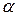 определяется из формулы (2). Во многих случаях известны величина и направле-ние поперечной нагрузки ( определяется из формулы (2). Во многих случаях известны величина и направле-ние поперечной нагрузки ( 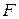 или или 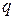 ), направлениях их будем определять углом ), направлениях их будем определять углом 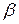 , отсчи-тываемый от оси , отсчи-тываемый от оси 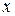 (рис. 7.6), (рис. 7.6), |
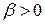 против хода часовой стрелки. В произвольном сечении балки на расстоянии
против хода часовой стрелки. В произвольном сечении балки на расстоянии 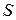 от торца от
от торца от 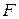 возникнет
возникнет 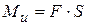 , который с направлением
, который с направлением 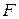 составляет угол 90°, а с осью
составляет угол 90°, а с осью 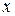 угол
угол 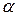 , т.е.
, т.е. 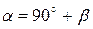 . Зная
. Зная 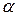 и
и 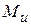 ,
, 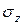 можно вычислять по (7.5). Но проще силу
можно вычислять по (7.5). Но проще силу 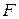 разложить по осям
разложить по осям 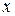 и
и 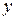 , т.е.
, т.е. 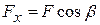 ,
, 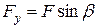 (видно из рис. 7.6). От
(видно из рис. 7.6). От 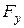 строят эпюру
строят эпюру 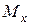 , а от
, а от 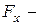 эпюру
эпюру 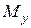 и далее
и далее 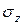 определяют по формуле (7.4). Аналогично и от погонной нагрузки
определяют по формуле (7.4). Аналогично и от погонной нагрузки 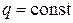 :
: 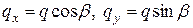 , от
, от 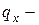 эпюру
эпюру 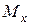 , от
, от 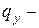 эпюру
эпюру 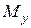 .
.
Нейтральная ось (Н.О)
Нейтральная ось – линия в сечении балки, относительно которой сечение поворачивается, оставаясь плоским (гипотеза Бернулли). Обозначим координаты точек на нейтральной оси через 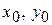 . Согласно определения Н.О в этих точках
. Согласно определения Н.О в этих точках 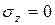 . Подставляя
. Подставляя 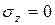 ,
, 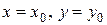 в (7.5), сокращая на
в (7.5), сокращая на 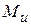 получим
получим
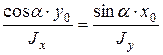 (3)
(3)
Это уравнение Н.О. Видно, что это уравнение прямой линии проходящей через начало координат, т.к. при 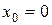 должно быть
должно быть 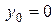 . Положение Н.О удобно определять через угол ее наклона к одной из осей координат. Обозначим
. Положение Н.О удобно определять через угол ее наклона к одной из осей координат. Обозначим 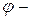 угол наклона Н.О к оси
угол наклона Н.О к оси 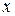 (рис. 7.7),
(рис. 7.7), 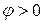 против хода часовой стрелки.
против хода часовой стрелки.
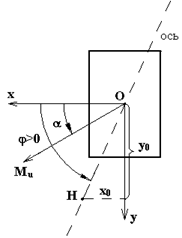 Рис.7.7 Рис.7.7 | Из рис. 7.7 видно 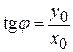 (4) Из (3) следует (4) Из (3) следует 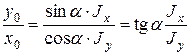 (5) С учетом (4) получим (5) С учетом (4) получим 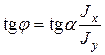 (7.6) Плоскость изгибающей нагрузки перпендику-лярна (7.6) Плоскость изгибающей нагрузки перпендику-лярна 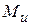 , а плоскость изгиба (прогибов) пер- , а плоскость изгиба (прогибов) пер- |
пендикулярна Н.О. При 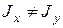 эти плоскости не совпадают
эти плоскости не совпадают 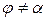 , поэтому эту деформацию и назвали «косой изгиб». При
, поэтому эту деформацию и назвали «косой изгиб». При 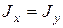 (сечение квадратное, круглое и т.д.)
(сечение квадратное, круглое и т.д.) 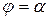 и косого изгиба не будет.
и косого изгиба не будет.
Определение напряжений. Расчеты на прочность.
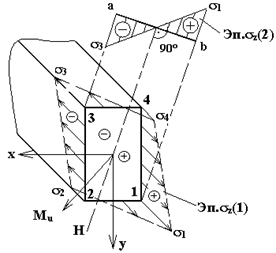 |
Рис.7.8
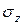 в аксонометрии (Эп.
в аксонометрии (Эп. 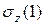 ) или в плоскости сечения (Эп.
) или в плоскости сечения (Эп. 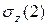 ), используя формулы (7.4) или (7.5), эпюры показаны на рис. 7.8. Для построения эпюр
), используя формулы (7.4) или (7.5), эпюры показаны на рис. 7.8. Для построения эпюр 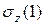 вычисляют
вычисляют 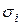 в угловых точках сечения (
в угловых точках сечения ( 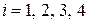 ) и откладывают их в масштабе с учетом знаков (
) и откладывают их в масштабе с учетом знаков ( 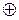 – растяжение, наружу от сечения, (–) – сжатие - противоположно).
– растяжение, наружу от сечения, (–) – сжатие - противоположно). 
Далее точки соединяют прямыми линиями, т.к. из (7.4) и (7.5) видно, что 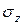 линейны по координатам
линейны по координатам 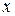 и
и 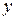 . Итак, Н.О делит сечение на две зоны, растянутую
. Итак, Н.О делит сечение на две зоны, растянутую 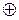 и сжатую (–) (рис. 7.8).
и сжатую (–) (рис. 7.8).
Для построение эпюры 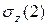 перпендикулярно Н.О проводят линию
перпендикулярно Н.О проводят линию 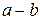 . В т. «
. В т. « 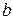 » в масштабе откладывают
» в масштабе откладывают 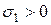 , а в т. «а»
, а в т. «а» 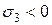 и далее соединяют их прямой линией.
и далее соединяют их прямой линией.
Из эпюр 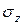 видно, что экстремальные напряжения возникают в точках сечения, наиболее удаленных от Н.О. Это будут т.1 и т.3. В них
видно, что экстремальные напряжения возникают в точках сечения, наиболее удаленных от Н.О. Это будут т.1 и т.3. В них 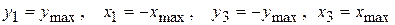 и по (7.4)
и по (7.4)
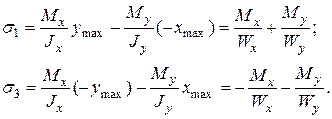 где
где 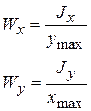
Итак, в т.1 и т.3 сечения 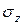 равны по величине и противоположны по знаку
равны по величине и противоположны по знаку
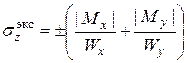 (7.7)
(7.7)
Здесь знак выбирают по физическому смыслу, 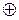 в растянутой зоне, (–) в сжатой. Аналогично определяются
в растянутой зоне, (–) в сжатой. Аналогично определяются 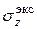 в других сечения с выступающими углами.
в других сечения с выступающими углами.
Для балок из пластичных материалов, одинаково работающих на растяжение и сжатие, условие прочности в опасном сечении бруса можно записать так с учетом (7.7)
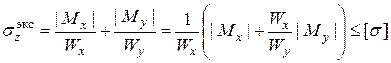 (7.8)
(7.8)
При подборе размеров сечения балки используем вторую формулу (7.8), при этом надо задать отношение 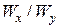 с учетом рационального расположения сечения: для прямоугольника при
с учетом рационального расположения сечения: для прямоугольника при 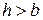 (размер
(размер 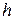 вдоль оси
вдоль оси 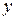 ) если
) если 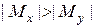 то
то 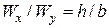 ; если
; если 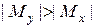 , то размер
, то размер 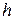 вдоль оси
вдоль оси 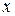 (т.е. повернуть на 90°) и
(т.е. повернуть на 90°) и 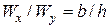 . Условие прочности одно, а неизвестных два
. Условие прочности одно, а неизвестных два 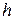 и
и 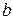 , поэтому сами задаем отношение
, поэтому сами задаем отношение 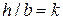 . Зная
. Зная 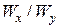 по (7.8) вычисляем необходимый
по (7.8) вычисляем необходимый 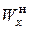 , а по нему размеры
, а по нему размеры 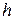 и
и 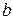 с учетом отношения
с учетом отношения 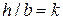 . При подборе стандартных двутавров и швеллеров аналогично: если
. При подборе стандартных двутавров и швеллеров аналогично: если 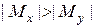 сечение располагаем вертикально, как в таблицах ГОСТа и берем: для двутавров
сечение располагаем вертикально, как в таблицах ГОСТа и берем: для двутавров 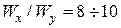 , для швеллеров
, для швеллеров 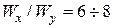 ; если
; если 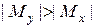 сечение располагаем горизонтально и для двутавров
сечение располагаем горизонтально и для двутавров 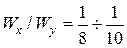 , для швеллеров
, для швеллеров 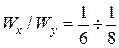 . Далее по (7.8) находимый необходимый
. Далее по (7.8) находимый необходимый 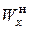 и по нему стандартный номер профиля (в первом случае
и по нему стандартный номер профиля (в первом случае 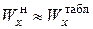 , во втором
, во втором 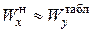 ). Определив номер профиля, делаем его проверку по первой формуле (7.8), подставляя табличные значения
). Определив номер профиля, делаем его проверку по первой формуле (7.8), подставляя табличные значения 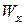 и
и 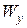 из ГОСТа с учетом вышеуказанного в скобках. Можно учесть
из ГОСТа с учетом вышеуказанного в скобках. Можно учесть 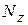 , добавив
, добавив 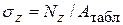 .
.
Для произвольного сечения условия прочности имеют вид 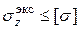 : надо найти наиболее удаленные от Н.О точки сечения, найти в них
: надо найти наиболее удаленные от Н.О точки сечения, найти в них 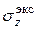 и сравнить их с допускаемыми.
и сравнить их с допускаемыми.
Для балок из хрупких материалов отдельно делается проверка прочности в растянутой (р) и сжатой (сж) зонах, т.к. для них 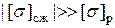 . Размеры произвольного сечения определяются методом попыток (подбором). При каждой попытке необходимо уточнить положение Н.О и координаты точек сечения с
. Размеры произвольного сечения определяются методом попыток (подбором). При каждой попытке необходимо уточнить положение Н.О и координаты точек сечения с 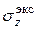 .
.
Определение прогибов
Определяют закон изменения прогибов 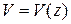 в плоскости
в плоскости 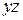 как указано в разделе 5, используя известное уравнение
как указано в разделе 5, используя известное уравнение 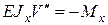 и метод Клебша. Далее определяют прогибы
и метод Клебша. Далее определяют прогибы 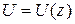 в горизонтальной плоскости
в горизонтальной плоскости 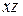 используя метод Клебша и аналогичное уравнение
используя метод Клебша и аналогичное уравнение 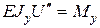 . Полный прогиб «
. Полный прогиб « 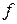 » в любом сечении балки найдем геометрическим сложеним прогибов
» в любом сечении балки найдем геометрическим сложеним прогибов 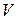 и
и 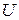 в каждом сечении:
в каждом сечении: 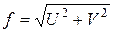 . Вычислив «
. Вычислив « 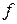 » в нескольких сечениях по длине балки, строят изогнутую ось балки и проверяют ее жесткость.
» в нескольких сечениях по длине балки, строят изогнутую ось балки и проверяют ее жесткость.
II. Внецентренное сжатие (растяжение)
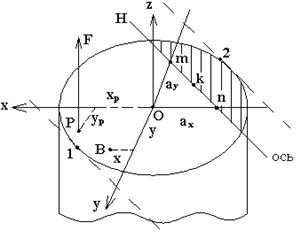 Рис.7.9 | Эта деформация возникает обычно в вертикальных брусьях и колоннах при действии на них продольных сил 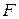 , приложенных в т. «Р» (полюс) не совпадающей с т. О – центром тяжести сечении (рис. 7.9). При переносе силы , приложенных в т. «Р» (полюс) не совпадающей с т. О – центром тяжести сечении (рис. 7.9). При переносе силы 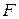 в т. О брус нагрузится продольной силой в т. О брус нагрузится продольной силой 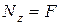 и изгибающим моментом и изгибающим моментом 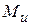 , причем все сечения бруса по его длине будут загружены одинаково. , причем все сечения бруса по его длине будут загружены одинаково. |
Определение напряжений
Пусть на брус в т. «Р» с координатами 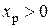 и
и 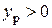 действует растягивающая сила
действует растягивающая сила 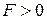 (рис. 7.9). Перенесем силу
(рис. 7.9). Перенесем силу 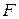 сначала на ось
сначала на ось 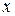 (плечо
(плечо 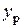 ), а затем в т. О (плечо
), а затем в т. О (плечо 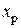 ). В итоге в поперечном сечении бруса возникнут:
). В итоге в поперечном сечении бруса возникнут:
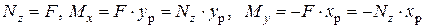 (6)
(6)
В произвольной точке «В» сечения с координатами 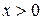 и
и 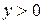
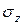 найдем по (7.2)
найдем по (7.2)
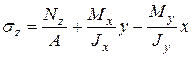 (7)
(7)
Подставляя (6) в (7) получим
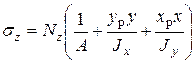 (7.9)
(7.9)
Учитывая, что 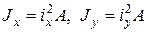 и подставляя в (7.9)
и подставляя в (7.9)
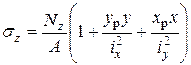 (7.10)
(7.10)
В произвольных случаях нагружения в формулы (7.9) и (7.10) 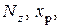
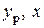 и
и 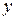 надо подставлять со своими знаками в заданных главных центральных осях
надо подставлять со своими знаками в заданных главных центральных осях 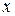 и
и 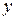 .
. 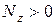 при растяжении бруса,
при растяжении бруса, 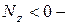 при сжатии.
при сжатии.
Эпюры 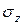 в сечении строятся аналогично как при косом изгибе.
в сечении строятся аналогично как при косом изгибе.
Нейтральная ось (Н.О)
Обозначим координаты точек на Н.О через 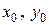 . В этих точках
. В этих точках 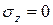 . Подставляя
. Подставляя 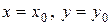 и
и 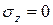 в (7.10) и сокращая на
в (7.10) и сокращая на 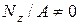 получим
получим
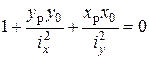 (7.11)
(7.11)
Это уравнение Н.О. Видно, что это уравнение прямой ( 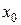 и
и 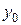 в первой степени), не проходящей через начало координат (т.к. при
в первой степени), не проходящей через начало координат (т.к. при 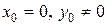 ). Положение Н.О удобно определять отрезками
). Положение Н.О удобно определять отрезками 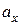 и
и 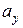 , которые Н.О отсекает на осях координат (рис. 7.9) и проходит через т. «
, которые Н.О отсекает на осях координат (рис. 7.9) и проходит через т. « 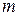 » и т. «
» и т. « 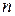 ». Допустим пока, что
». Допустим пока, что 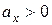 и
и 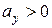 . Точка «
. Точка « 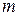 » в этом случае имеет координаты
» в этом случае имеет координаты 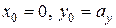 . Подставляем это в (7.11) получим
. Подставляем это в (7.11) получим
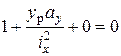
Отсюда
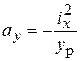 (7.12а)
(7.12а)
Аналогично т. « 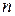 ». Подставляя
». Подставляя 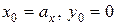 найдем
найдем
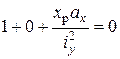
Отсюда
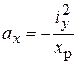 (7.12в)
(7.12в)
Из (7.12) видно, что при 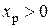 и
и 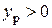 получим
получим 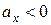 и
и 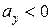 , т.е. наше допущение неверно и правильно Н.О показана на рис. 7.9.
, т.е. наше допущение неверно и правильно Н.О показана на рис. 7.9.
Свойства нейтральной оси
Из формул (7.12) следует:
1. Положение Н.О не зависит от величины и знака 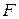 .
.
2. Н.О и полюс т. «Р» лежат по разные стороны от центра тяжести сечения т. О.
3. При удалении полюса от т. О, Н.О приближается к нему и наоборот.
4. Если полюс расположен на одной из осей координат, то Н.О перпендикулярна к этой оси (при 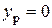 полюс на оси
полюс на оси 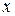 ,
, 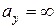 , т.е. Н.О параллельна оси
, т.е. Н.О параллельна оси 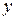 или перпендикулярна оси
или перпендикулярна оси 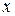 ).
).
5. При вращении Н.О вокруг произвольной точки « 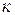 » на ней (рис. 7.9), полюс перемещается по прямой линии, не проходящей через т. О. Подставим в (7.11)
» на ней (рис. 7.9), полюс перемещается по прямой линии, не проходящей через т. О. Подставим в (7.11) 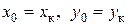 . Получим уравнение, которое относительно координат
. Получим уравнение, которое относительно координат 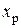 и
и 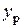 есть уравнение прямой не проходящей через т. О.
есть уравнение прямой не проходящей через т. О.
6. Н.О делит сечение на две зоны: растянутую и сжатую, заштрихованную на рис. 7.9 при 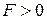 .
.
Из соотношений (7.12) можно решить обратную задачу: зная положение Н.О (т.е. 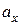 и
и 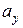 ) найти положение полюса, т.е.
) найти положение полюса, т.е. 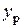 и
и 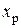
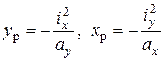 (7.13)
(7.13)
Расчеты на прочность
Определив положение Н.О, проведем к контуру сечения касательные, параллельные Н.О. Получим т.1 с координатами 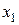 и
и 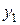 и т.2 с координатами
и т.2 с координатами 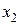 и
и 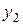 . Если в т. «Р» действует
. Если в т. «Р» действует 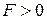 , то в т. 1 будут
, то в т. 1 будут 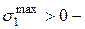 растягивающие (р), а в т. 2
растягивающие (р), а в т. 2 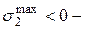 сжимающие (сж). Обычно колонны изготавливают из хрупких материалов, поэтому прочность проверяется отдельно в растянутой и сжатой зонах по формулам (7.9) или (7.10):
сжимающие (сж). Обычно колонны изготавливают из хрупких материалов, поэтому прочность проверяется отдельно в растянутой и сжатой зонах по формулам (7.9) или (7.10):
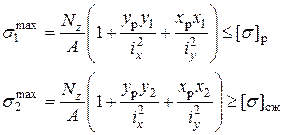 (8)
(8)
При действии на колонну сжимающей силы 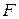 в т. 1 будут
в т. 1 будут 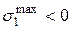 , в т. 2
, в т. 2 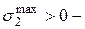 растягивающие.
растягивающие.
Размеры сечения обычно определяются методом подбора: задают размеры, определяют положение Н.О, т.1 и т.2 и проверяют в них прочность по (8). Если эти условия не выполняются, меняют размеры сечения и снова проверяют.
Для брусьев с сечениями типа прямоугольника, двутавра или швеллера из пластичных материалов, у которых 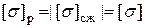 , первую попытку можно провести как при косом изгибе по второй формуле (7.8), определив
, первую попытку можно провести как при косом изгибе по второй формуле (7.8), определив 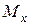 и
и 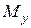 по (6), а
по (6), а 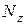 пока не учитывать. Здесь подбор размеров сечения проводить так, как указано ниже формулы (7.8). Определив размеры сечения, делать проверку по (8) с учетом
пока не учитывать. Здесь подбор размеров сечения проводить так, как указано ниже формулы (7.8). Определив размеры сечения, делать проверку по (8) с учетом 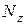 .
.
Ядро сечения
Для колонн из хрупких материалов (чугун, бетон, камень и т.д.), плохо работающих на растяжение желательно, чтобы от сжимающей силы 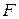 во всех точках сечения были только сжимающие напряжения. Этого можно добиться, если Н.О не пересекает сечение колонны, а согласно свойства 3 Н.О. это получим, ограничивая удаление полюса «Р» от т. О.
во всех точках сечения были только сжимающие напряжения. Этого можно добиться, если Н.О не пересекает сечение колонны, а согласно свойства 3 Н.О. это получим, ограничивая удаление полюса «Р» от т. О.
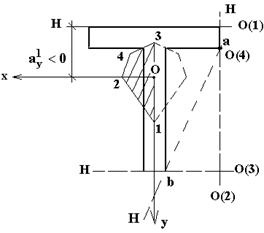 Рис.7.10 Наши рекомендации
|