Классификация величин. Все реальные объекты характеризуются своими свойствами

Все реальные объекты характеризуются своими свойствами. Свойство – философская категория, выражающая такую сторону объекта (явления, процесса), которая обуславливает его различие или общность с другими объектами (явлениями, процессами) и обнаруживается в его отношениях к ним. Свойство – это категория качественная. Для количественного описания различных свойств процессов и физических тел вводится понятие величины. Величина – это свойство чего-либо, которое может быть выделено среди других свойств и оценено тем или иным способом, в том числе и количественно.

Анализ величин позволяет разделить их на два вида (рис. 1).

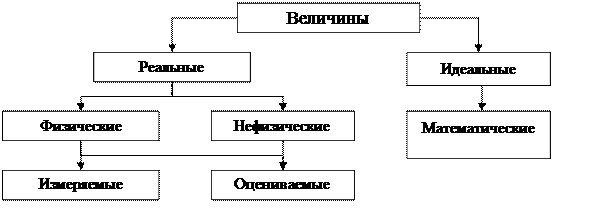
Рис. 1. Классификация величин

Выделяют два вида величин: реальные и идеальные. Идеальные величины используются в математике.

Реальные величины делятся на физические и нефизические. Физические величины используются в естественных (физика, химия) и технических науках. Нефизические величины присущи гуманитарным наукам (философия, социология и т. д.).

Физические величины в свою очередь делятся на измеряемые и оцениваемые. Измеряемые ФВ выражены числом данной единицы измерения. Если ФВ не обладает единицей измерения, то она может быть только оценена. Оценивание величины – это операция приписывания данной величине определенного числа, проводимая по установленным правилам. При оценивании используют шкалы (например, скорость ветра оценивают по шкале Бофорта). Отметим, что нефизические величины могут быть только оценены.

Физической величиной называют одно из свойств физического объекта (физической системы, явления или процесса), общее в качественном отношении для многих физических объектов, но в количественном отношении индивидуальное для каждого из них (ГОСТ 16263–70). Например, плотностью характеризуют многие твердые и жидкие вещества и материалы, хотя каждый из образцов материалов и веществ имеет свою конкретную величину плотности. Также и свойство «прочность» в качественном отношении характеризует такие материалы, как сталь, дерево, ткань, стекло и многие другие, в то время как степень (количественное значение) прочности – величина для каждого из них совершенно разная.

Качественная сторона понятия «физическая величина» определяет «род» величины (длина, как характеристика протяженности вообще; электрическое сопротивление, как общее свойство проводников электричества и т. п.), а количественная – ее «размер» (длина конкретного предмета, сопротивление конкретного проводника). Размер физической величины существует объективно, независимо от того, знаем мы его или не знаем.

Все процессы в природе обусловлены возможностью обмена энергией или веществом. С этой точки зрения ФВ можно разделить по видам явлений:

§ вещественные (описывающие свойства веществ такие как масса, объем, электрическое сопротивление и т.д.);

§ энергетические (описывающие процессы преобразования, передачи и использования энергии);

§ характеризующие протекание процессов во времени (спектральные характеристики, корреляционные функции и др.) (рис. 2).

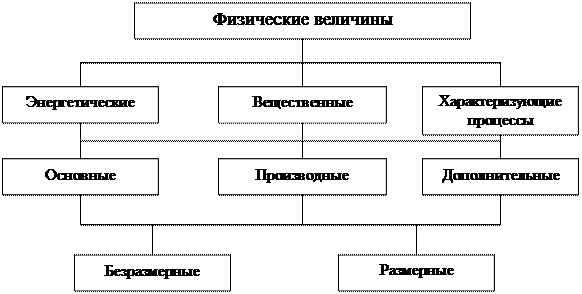
Рис. 2. Классификация ФВ

По степени условной независимости от других величин ФВ делятся:

§ основные – это физические величины, входящие в систему и условно принятые в качестве независимых от других величин этой системы. В качестве единиц основных физических величин применяют основные единицы ФВ системы СИ.

Основными физическими величинами считаются:

1) длина: L = [м] (метр),

2) масса: M = [кг] (килограмм),

3) время: T = [с] (секунда),

4) сила электрического тока: I = [А] (ампер),

5) термодинамическая температура: θ = [К] (кельвин),

6) сила света: J = [кд] (кандела),

7) количество вещества: N = [моль].

§ производные – это ФВ, образуемые по определяющим уравнениям, состоящим из других ФВ данной системы. Например: давление [Па], мощность [Вт].

§ дополнительные: плоский и телесный углы. Плоский угол измеряется в радианах, а телесный – в стерадианах.

Радиан – это плоский угол с вершиной в центре окружности, стягиваемый дугой, равной по длине радиусу этой окружности.

Стерадиан – это телесный угол с вершиной в центре сферы, стягиваемый сферической поверхностью, равной по площади квадрату радиуса сферы.

Примечание: в 1995 г. XX ГКМВ (Резолюция 8) постановила исключить класс дополнительных единиц в СИ, а радиан и стерадиан считать безразмерными производными единицами СИ, имеющими специальные наименования и обозначения. (ГОСТ 8.417-2002).

По наличию размерности ФВ делятся на размерные и безразмерные.

Размерность является качественной характеристикой измеряемой величины и обозначается символом dim, происходящим от слова dimension. Размерность основных физических величин обозначаются соответствующими заглавными буквами (dim l = L, dim t = T и т.д.).

При определении размерности производных величин руководствуются следующими правилами:

1. Размерность левой и правой части уравнений не могут не совпадать, так как сравниваться могут только одинаковые свойства. Объединяя, левые и правые части уравнений, можно прийти к выводу, что алгебраически суммироваться могут только величины, имеющие одинаковые размерности.

2. Алгебра размерностей мультипликативна, то есть состоит из одного единственного действия – умножения.

· Размерность произведения нескольких величин равна произведению их размерностей. Так, если зависимость между значениями величин Q, A, B, C имеет вид Q = A∙B∙C то, dim Q = dim A∙ dim B∙dim C,

· Размерность частного при делении одной величины на другую равна отношению их размерностей, то есть если Q = A/B, то dim Q = dim A /dim B,

· Размерность любой величины, возведенной в некоторую степень, равна такой же степени ее размерности. Так, если Q = A ⁿ , то dim Q = dim ⁿ A.

Всегда можно выразить размерность производной ФВ через размерность основных физических величин с помощью степенного одночлена:

,

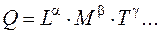где L, M, T – размерности соответствующих основных физических величин; α, β, γ – показатели размерности. Каждый из показателей размерности может быть положительным или отрицательным, целым или дробным числом, нулем. Если все показатели размерности равны нулю, то такая величина называется безразмерной. Она может быть относительной, определяемой как отношение одноименных величин (например, относительная диэлектрическая проницаемость), и логарифмической, определяемой как логарифм относительной величины (например, логарифм отношения мощностей или напряжений). В гуманитарных науках, искусстве, спорте, квалиметрии, где номенклатура основных величин не определена, теория размерностей не находит пока эффективного применения.