Краткие сведения из теории. 1. Постоянные величины. Абсолютные постоянные и параметры.Величина называется постоянной, если она всегда или только в условиях данной задачи сохраняет одно и

1. Постоянные величины. Абсолютные постоянные и параметры.Величина называется постоянной, если она всегда или только в условиях данной задачи сохраняет одно и то же числовое значение.

Постоянные величины разделяются на абсолютные постоянные величины и параметры. Величина, которая сохраняет одно и то же значение при всех условиях, называется абсолютной постоянной (примерами абсолютных постоянных являются. все числа, сумма внутренних углов треугольника, число 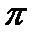; скорость света в пустоте)

Параметром насевается такая постоянная величина, которая лишь в условиях данной задачи (данного исследования) сохраняет постоянное, вполне определенное числовое значение, но с изменением условий задачи принимает уже другое, хотя опять таки определенное числовое значение.

2. Переменные величины.Величина называется переменной, если она в условиях данной задачи принимает различные числовые значения.

3. Независимые переменные. Две переменные величины называются независимыми, если значения, переменные одной из них, не зависит от значений, принимаемых другой.

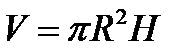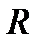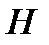(Пример: в формуле для определения объема цилиндра величины и —независимые переменные, так как значения, принимаемые высотой 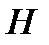цилиндра, не зависят от значений 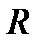, которые принимает радиус цилиндра).

4. Функция. Переменная величина 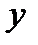Называется функцией от переменной величины 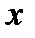по известному правилу или закону

соответствует одно определенное значение 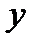. [2]Если переменная величина 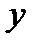является функцией переменной величины 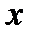, то это обозначают так:

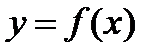(2.1)

Эта запись читается: «игрек есть функция от иск», или «игрек равен эф от икс».

В записи (2.1) 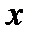называется аргументом или независимой переменной, а 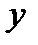—функцией, или зависимой переменной.

5. Задание функции.Функция (2.1)считается заданной, если:

1) Указана совокупность всех рассматриваемых значений аргумента .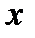

2) Указан закон, который позволяет по заданному значению аргумента 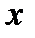находить соответствующее ему значение функции .

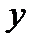6. Частым значением функцииназывается то ее значение, которое соответствует частому значению аргумента 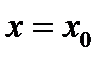. Для обозначения частого значения функции при 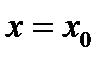употребляется символ 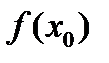или .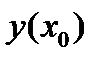

7. Область существования функции.Если функция задана аналитически, то областью существования функции (иначе, областью определения функции) называется совокупность тех действительных значений аргумента, при которых аналитическое выражение, определяющее функцию, не теряет числового смысла и принимает только действительные значения.