Принцип относительности классической механики

Если подвижная система координат движется поступательно, равномерно и прямолинейно, то переносная 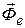и Кориолисова 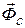силы инерции будут равны нулю, и основное уравнение динамики относительного движения ничем не будет отличаться от основного уравнения динамики для абсолютного движения.

Таким образом, движение точки по отношению к подвижной системе отсчета, движущейся, поступательно, прямолинейно и равномерно, происходит также, как и по отношению к неподвижной системе отсчета.

Никакие механические явления, происходящие в среде, не могут обнаружить ее прямолинейного, равномерного и поступательного движения.

Условие относительного покоя.

Рассмотрим случай, когда материальная точка неподвижна относительно подвижной системы отсчета, т.е.

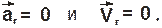
Тогда

Таким образом,

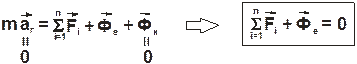
В случае, когда материальная точка находится в состоянии покоя относительно подвижной системы отсчета, то геометрическая сумма действующих на точку активных сил и переносной силы инерции равна нулю.

Методика решения задач

1. Установить, какое движение для точки является переносным, какое - относительным.

2. Изобразить активные силы, действующие на точку.

3. Определить переносную и Кориолисову силы инерции и присоединить эти силы к активным силам.

4. Составить дифференциальные уравнение относительного движения.

5. Проинтегрировать дифференциальные уравнения, определив постоянные интегрирования по начальным условиям движения точки.

6. Определить искомые величины.

Условие задачи. Составить уравнение относительного движения шарика массой m, перемещающегося по гладкому пазу горизонтального диска (рис.3.17), вращающегося вокруг вертикальной оси с постоянной угловой скоростью w. При t=0 x=x₀ и v=v₀. Определить давление шарика на стенку канала в произвольный момент времени. Силами сопротивления движению пренебречь.

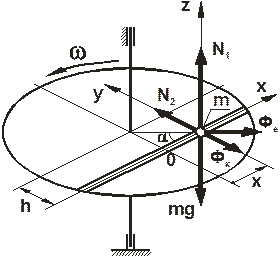
Рис.3.17

Решение. Вращение диска вокруг оси - переносное движение, движение точки по диску - относительное движение.

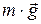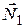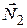На точку в процессе движения действует сила тяжести и нормальная реакция стенки паза, составляющие которой обозначены и . К названным силам присоединяем переносную 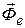и Кориолисову 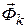силы инерции. Направление сил показано на схеме.

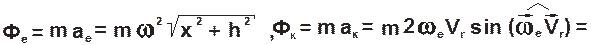
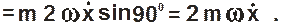
Составляем дифференциальное уравнение относительного движения:

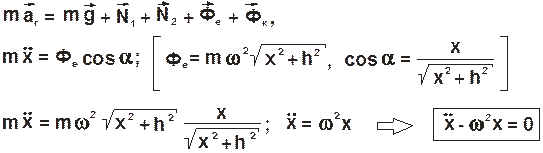(2.7)

Решением полученного дифференциального уравнения является выражение вида:

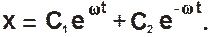
Для определения постоянных С₁ и С₂ найдем

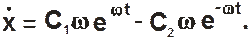
Подставив начальные условия в полученные выше выражения, получим:

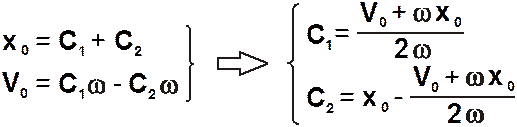
Таким образом, с учетом значений С₁ и С₂ уравнение относительного движения шарика будет иметь следующий вид:

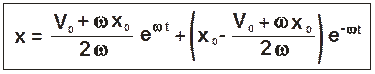
Давление шарика на стенку определим, спроектировав векторное выражение (2.7) на оси z и y:

Учитывая, что

.
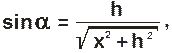
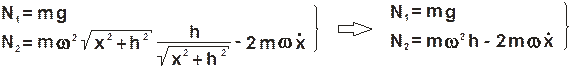
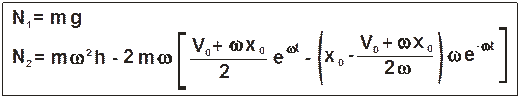
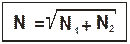