Вариационные ряды и их графическое изображение

Вариациейназывается различие значений признака у отдельных единиц изучаемой совокупности в один и тот же период или момент времени.

Статистический анализ вариации предполагает:

1. Построение вариационного ряда

2. Графическое изображение вариационного ряда

3. Расчет основных характеристик вариационного ряда.

Построение вариационного ряда (ряд распределения) – это упорядоченное распределение единиц совокупности по возрастающим или убывающим значениям признака.

В составе любого вариационного ряда можно выделить три основных элемента: варианта, частота и частость.

Варианта– это значения, которые принимает исследуемый признак и обозначается через x.

Частоты вариационного ряда – абсолютная численность отдельных групп с различными значениями признака, обозначается через m.

Частости вариационного ряда – удельные веса (доли) отдельных групп в общей совокупности.

Вариационные ряды бывают двух видов:

- дискретные;

- интервально-вариационные.

В дискретных рядах варианты представлены в виде целочисленных величин. Если варианты представлены в виде интервалов, то такие ряды называются интервально-вариационными.

Для анализа вариационных рядов и определения формы распределения используются графики. При графическом изображении вариационного ряда в статистике используется полигон распределения, гистограмма и кумулята.

Чтобы построить полигон распределения на оси абсцисс отмечают точки, соответствующие величине вариант значений признака из них восстанавливаются перпендикуляры, длине которых соответствует частота этих вариант по принятому масштабу на оси ординат. Вершины перпендикуляров соединяются отрезками прямой.

Первым этапом изучения вариационного ряда является его графическое изображение.Дискретный вариационный ряд изображается в виде так называемого полигона, или многоугольника, распределения частот, являющегося разновидностью статистических ломаных. Для изображения интервального ряда применяются полигонраспределения частот и гистограмма частот.

Строятся графики в прямоугольной системе координат. При построении полигона частот на оси абсцисс в одинаковом масштабе откладываются направо в порядке возрастания значения признака (для дискретного характера) или центральные значения интервалов (для интервальных рядов); по оси ординат наносится шкала для выражения величин частот. Из точек на оси абсцисс, соответствующих величине признака, восстанавливаются перпендикуляры высотой, соответствующей частоте; вершины перпендикуляров соединяются отрезками прямой. Крайние точки полученной ломаной соединяются с лежащими на оси абсцисс следующими (меньшими и большими) возможными, но фактически не наблюдающимися значениями признака, частота которых, очевидно, равна 0. Замкнутая с осью абсцисс ломаная линия представляет полигон распределения частот. Построим полигон частот по табл. 4.4. (рис.4.1)

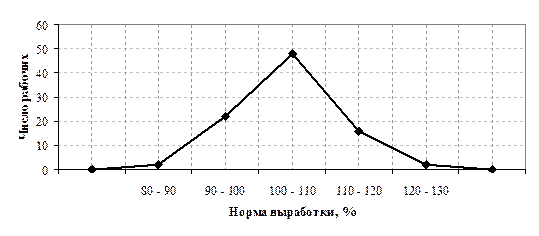
Рис. 4.1 – Полигон распределения рабочих по выполнению норм выработки

Для построения гистограммы по оси абсцисс откладывают величины интервалов, а частоты изображаются прямоугольниками, построенными на интервалах с высотой в масштабе оси ординат (рис. 4.2). В случае неравенства интервалов гистограмма строится не по частотам или частостям, а по плотности распределения.

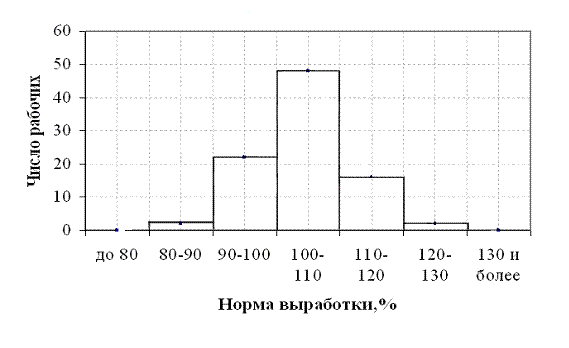
Рис. 4.2 – Гистограмма распределения рабочих по выполнению норм выработки

В ряде случаев для изображения вариационных рядов используется кумулятивная кривая (кумулята (рис.4.3), она особенно удобна для сравнения вариационных рядов. Накопленные частоты наносятся на чертеж в виде ординат; соединяя вершины отдельных ординат прямыми, получают ломаную линию, которая, начиная с нуля, непрерывно поднимается над осью абсцисс, до тех пор пока не достигнет высоты, соответствующей общей сумме частот.

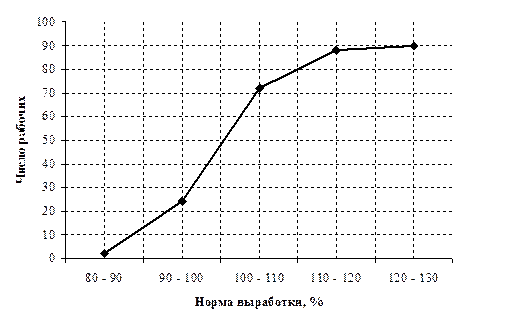
Рис. 4.3 – Кумулята распределения рабочих по выполнению норм выработки

Если поменять местами оси координат в кумуляте, то получаем новый вид графического изображения - огиву.

При построении графических изображений вариационного ряда большое значение имеет соотношение масштабов по оси абсцисс (х) и оси ординат (f). В этом случае следует руководствоваться так называемым «правилом золотого сечения», в соответствии с которым высота графика должна быть примерно в два раза меньше его основания.

22 Числовые характеристики выборочной совокупности: выборочное среднее, дисперсия, мода и медиана, начальные и центральные моменты.

для изучения основных свойств статистического распределения используют выборочные числовые характеристики. Для нахождения центра распределения вычисляют различные типы средних величин, моду и медиану, степени вариации-размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации и другие величины.

1. Выборочная средняя арифметическая:

(1)

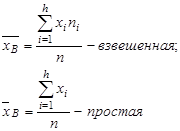
2. Выборочная средняя квадратическая:

(2)

3. Выборочная средняя геометрическая:

(3)

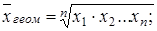
При вычислении различных типов средних величин для одного и того же вариационного ряда всегда имеем

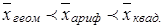
Эти неравенства характеризуют свойство мажорантности средних.

Для упрощения вычисления выборочной средней арифметической удобно переходить от данных вариант 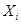условным вариантам 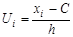где h- разность между соседними вариантами, 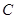- ложный нуль (варианта с наибольшей частотой): 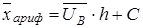(4)

4. Модой М₀ называется варианта, имеющая наибольшую частоту.

5. Медианой М_е называется такая варианта, которая делит вариационный ряд распределения на две равные части, т.е. варианта, находящаяся в середине ряда распределения.

Если в дискретном вариационном ряду 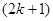значений, то .

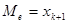Если число вариант четное 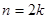, то медиана определяется как среднее арифметическое из двух серединных значений, т.е. .

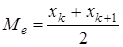6. Размах вариации 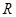определяется как разность между максимальным и минимальным вариантами, т.е.

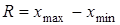. (5)

7. Среднее линейное отклонение – это средняя арифметическая из абсолютных значений отклонений вариант от средней арифметической

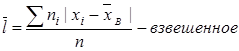(6)

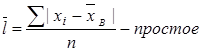
8. Дисперсиейназывается средний квадрат отклонения всех значений признака от его средней величины.

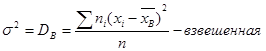(7)

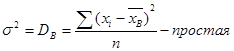
9. Исправленная дисперсия 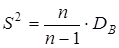(8)

10. Среднее квадратическое отклонение равно квадратному корню из дисперсии:

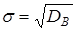(9)