ПИД-регулятор
Изменение свойств САУ путем введения корректирующих звеньев возможно, если известны характеристики элементов системы, подлежащие коррекции. Однако практика конструирования САУ различного назначения позволила найти общие принципы управления, применение которых обеспечивает требуемые качества САУ даже в отсутствие полной информации о свойствах системы.
Одним из самых распространенных классов САУ являются системы автоматического регулирования, задача которых заключается в поддержании текущего значения выходной величины объекта на заданном уровне. Устройство управления, которое в этом случае называют регулятором, формирует управляющее воздействие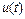 
в соответствии с некоторым алгоритмом.
Наибольшее применение в системах управления по отклонению получил алгоритм, носящий название пропорционально-интегро-дифференцирующего закона регулирования:
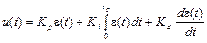, (3.2)
где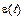 
– сигнал ошибки (рассогласования);
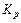– коэффициент усиления пропорциональной части управления;
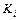– коэффициент усиления интегральной части управления;
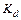– коэффициент усиления дифференциальной части управления;
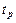– время регулирования.
В системах автоматического регулирования в зависимости от вида используемой коррекции регуляторы классифицируются на следующие типы: пропорциональный (П), интегрирующий (И), пропорционально-интегрирующий (ПИ), пропорционально-дифференциру-ющий (ПД) и пропорционально-интегро-дифференцирующий (ПИД) регуляторы. Соответственно говорят об одноименных алгоритмах или законах регулирования.
Таким образом, САР можно рассматривать как систему с отрицательной обратной связью, для улучшения характеристик которой применяют последовательное корректирующее звено в виде ПИД-ре-гулятора или его вариантов (рисунок 3.4).
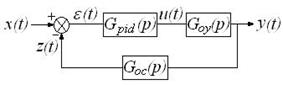
Рисунок 3.4 – ПИД-регулятор в составе САР
Пример 19. Оценить влияние П-регулятора на точность системы управления с единичной обратной связью в составе инерционного звена 1-го порядка с передаточной функцией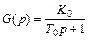 
.
Передаточная функция замкнутой системы примет вид
,
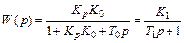где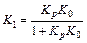 
, 
.
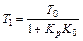Для проверки системы наточность подадим на ее вход ступенчатый сигнал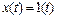 
и рассчитаем значение ошибки 
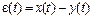в установившемся состоянии по соотношению
.
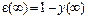Для определения выходного сигнала в установившемся состоянии воспользуемся теоремой о конечных значениях:
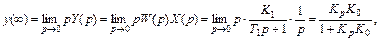откуда окончательно получим
.
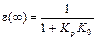Из данной формулы видно, что для уменьшения установившейся ошибки необходимо выбрать коэффициент усиления 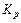регулятора как можно большим. Однако в реальных системах 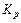является величиной ограниченной, поэтому добиться с помощью пропорционального регулятора абсолютной точности, когда 
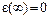, невозможно.
Пример 20.Оценить влияние И-регулятора на устойчивость системы управления с единичной обратной связью в составе инерционного звена 1-го порядка с передаточной функцией .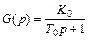
Передаточная функция замкнутой системы примет вид:
.
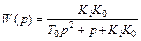Для анализа устойчивости системы рассмотрим ее характеристическое уравнение
,
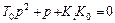где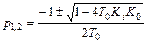 
– корни уравнения.
Порядок системы увеличился до 2-го, однако коэффициенты характеристического уравнения остались строго положительными, что достаточно для устойчивости.
С увеличением коэффициента усиления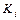 
регулятора дискриминант характеристического уравнения может стать отрицательным 
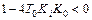, в результате чего его корни примут комплексный сопряженный вид, что соответствует затухающему колебательному режиму в системе.
Таким образом, И-регулятор увеличил порядок системы и может изменить тип переходных процессов. В рассматриваемом примере это не привело к потере устойчивости, однако с увеличением порядка объекта управления это вполне возможно.
ЛИТЕРАТУРА
1. Шишмарев, В.Ю. Основы автоматического управления: учебное пособие / В.Ю. Шишмарев. – М.: Академия, 2008. – 348 с.
2. Софиева, Ю.Н. Основы линейной теории автоматического регулирования / Ю.Н. Софиева, В.Я. Бадеников, А.Э. Софиев. – Иркутск: Изд-во Иркут. ун-та, 1994. – 124 с.
3. Юревич, Е.И. Теория автоматического управления / Е.И. Юревич. – Л.: Энергия, 1975. – 416 с.
4. Бесекерский, В.А. Теория систем автоматического регулирования / В.А. Бесекерский, Е.П. Попов. – М.: Наука, 1975. – 767 с.
5. Иванов, В.А. Математические основы теории автоматического регулирования / В.А. Иванов, Б.К. Чемоданов, В.С. Медведев. – М.: Высшая школа, 1971. – 807 с.
Учебное издание
Гареева Рената Гегелевна
ОСНОВЫ ТЕОРИИ УПРАВЛЕНИЯ
Методические рекомендации к практическим занятиям
по дисциплине «Основы теории управления»
Редактор Соловьева С.В.
Подписано в печать 17.12.2010. Формат 60´84 1/16
Усл. п. л. - 2,6. Уч.-изд. л. - 2,8
Печать - ризография, множительно-копировальный
аппарат «RISO EZ300»
Тираж 75 экз. Заказ 2011-15
Издательство Алтайского государственного
технического университета
656038, г. Барнаул, пр-т Ленина, 46
Оригинал-макет подготовлен ИИО БТИ АлтГТУ
Отпечатано в ИИО БТИ АлтГТУ
659305, г. Бийск, ул. Трофимова, 27
| |