Понятия статистической и корреляционной связи

Различают два типа связей между различными явлениями: функциональную или жестко детерминированную и статистическую или стохастически детерминированную.

Если с изменением значения одной переменной вторая меняется строго определенным образом, т.е. значение одной переменной обязательно соответствует одно или несколько точно заданных значений другой переменной, связь между ними является функциональной.

Стохастически детерминированная связь не имеет ограничений и условий, присущих функциональной связи. Если с изменением значения одной из переменных вторая может в определенных пределах принимать любые значения с некоторыми вероятностями, но её среднее значение или статистические массовые характеристики изменяются по определенному закону - связь является статистической.

Корреляционной связью называют важнейший частный случай статистической связи, который состоит в том, что разным значениям одной переменной соответствуют различные средние значения другой. С изменением значения признака х закономерным образом изменяется среднее значение у.

Поскольку корреляционная связь является статистической, первым условием возможности её изучения является общее условие всякого статистического исследования: наличие данных по достаточно большой совокупности явлений. Вторым условием изучения корреляционной связи служит достаточно качественная однородность совокупности. Третьим условием является необходимость подчинения распределения совокупности по результативному и факторным признакам нормальному закону. На практике эта предпосылка чаще всего выполняется приближенно, но и тогда получают неплохие результаты статистического изучения.

Изучение корреляционной связи имеет 2 цели:

1) измерение параметров уравнения, выражающего связь средних значений зависимой переменной со значениями независимой переменной.

2) измерение тесноты связи двух (или большего числа) признаков между собой.

В статистике принято различать следующие зависимости:

1. Парная корреляция - связь между 2 признаками (результативным и факторным или двумя факторными)

2. Частная корреляция - зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков.

3. Множественная корреляция - зависимость результативного и двух и более факторных признаков, включенных в исследование.

Корреляционный анализимеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи). Теснота связи количественно выражается величиной коэффициентов корреляции. Эти коэффициенты дают возможность количественно определить "полезность" факторных признаков при построении уравнений множественной регрессии, а также служат оценкой соответствия уравнения регрессии выявленным причинно-следственным связям..

Регрессионный анализзаключается в определении аналитического выражения связи, в котором изменение одной величины обусловлено влиянием одной или несколько независимых величин, а множество всех факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения. Регрессия может быть однофакторной (парной) и многофакторной (множественной).

Одной из проблем построения уравнения регрессии является её размерность, т.е. определение числа факторных признаков, включаемых в модель. Их число должно быть оптимальным. Практика выработала критерий, позволяющий установить количество факторных признаков, включаемых в модель. Число факторных признаков (k) должно быть в 5-6 раз меньше объема изучаемой совокупности.

По форме зависимости различают:

1) линейную регрессию, которая выражается уравнением прямой, вида:

3) нелинейную регрессию, которая выражается уравнениями вида:

парабола - ;

гипербола -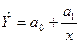

По направлению связи различают:

1) прямую регрессию (положительную), возникающую при условии, если с увеличением или уменьшением независимой величины значения зависимой также соответственно увеличиваются или уменьшаются.

2) обратную (отрицательную) регрессию, появляющуюся при условии, что с увеличением или уменьшением независимой величины, зависимая соответственно уменьшается или увеличивается.

Корреляция и регрессия тесно связаны между собой: первая оценивает силу статистической связи, вторая исследует её форму.

Парная корреляция

Корреляция– это статистическая зависимость между случайными величинами, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.

Различают парную, частную и множественную корреляцию.

Парная корреляция – это связь между двумя признаками (результативным и факторным или между двумя факторными).