Порядок построения диаграммы. Все современные табличные процессоры имеют в своем составе средства графического представления данных

ПОСТРОЕНИЕ ДИАГРАММ В EXCEL

Основные понятия

Все современные табличные процессоры имеют в своем составе средства графического представления данных, которые позволяют наглядно отобразить большие массивы числовой информации, значительно упростить их восприятие, решать задачи сравнения данных, поиска закономерностей и др. Поскольку графические средства в электронных таблицах выполняют деловые функции, они получили название средств деловой графики.

Диаграмма строится на основе рядов данных и представляет собой объект, внедренный на рабочий лист. Ряд – это последовательность (набор) однотипных данных. Ряды данных могут быть заданы как по строкам, так и по столбцам. Признак, определяющий соответствующие значения в рядах, называется категорией. Обычно категории отсчитываются по горизонтальной оси системы координат диаграммы, значения рядов – по вертикальной оси.

Обозначения категорий данныхотображаетлегенда.

Диапазон значений диаграммы определяется автоматически на основе имеющихся данных. Диаграмма сохраняет связь с данными, на основе которых она построена, при обновлении этих данных она немедленно изменит свой вид.

Типы диаграмм

В Excel существует множество типов диаграмм. Наиболее часто встречаются следующие:

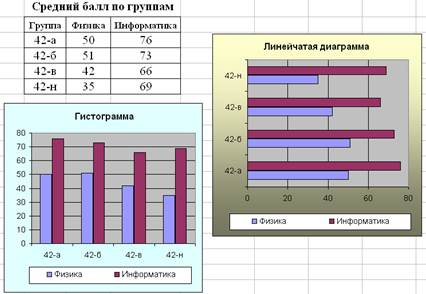
– обычная гистограмма и линейчатая диаграмма отображают значения различных категорий и удобны для иллюстрации соотношения величин:

– круговая диаграмма отображает вклад каждого значения (одного ряда данных) в общую сумму:

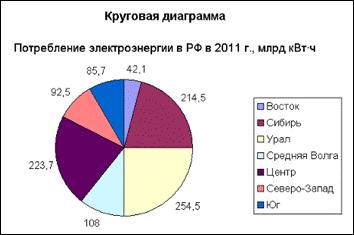
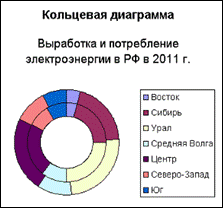
– кольцевая диаграмма, в отличие от круговой, может отражать
несколько рядов данных:

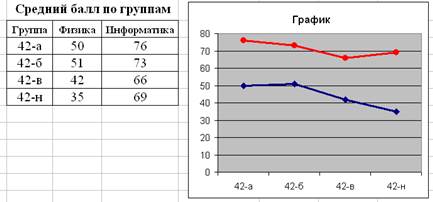
– графикотображает развитие процесса во времени или по категориям:

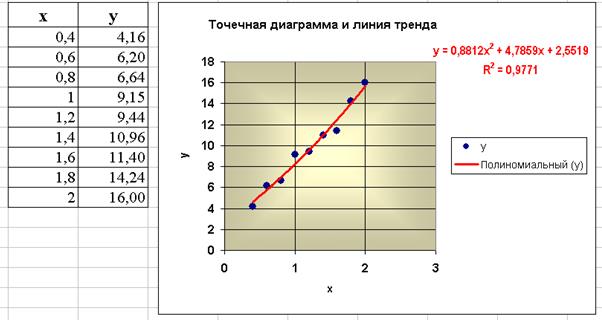
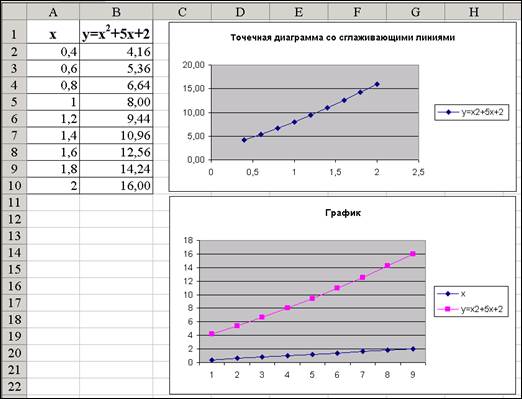
– точечная диаграмма отображает взаимосвязь между числовыми значениями в нескольких рядах данных. При построении зависимости функции от значений аргумента следует выбирать именно этот тип диаграммы (обычно используется Точечная со сглаживающими линиями). При выборе в этом случае типа диаграммы «График» вместо значений по оси абсцисс будут указаны их порядковые номера, что потом дает неверные результаты при определении линии тренда.

Элементы диаграммы

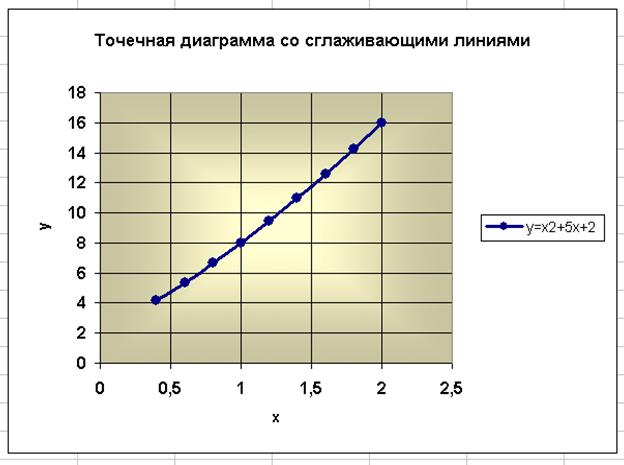
Порядок построения диаграммы

Для построения диаграммы обычно используют мастер диаграмм, где в пошаговом режиме выполняют все необходимые действия. Порядок работы при этом следующий.

1. Выделить строки или столбцы, содержащие данные для построения диаграммы, в том числе заголовки. Если данные не образуют единой группы, то список рядов данных задают позже на втором шаге мастера диаграмм, на вкладке Ряд в окне Исходные данные.

2. Запустить мастер диаграмм.

Способ 1: Меню Вставка → Диаграмма.

Способ 2: Щелкнуть кнопку Мастер диаграмм.

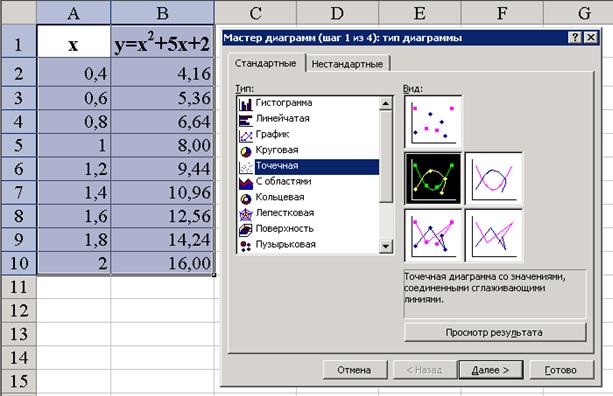
3. Шаг 1 мастера диаграмм: выбрать тип диаграммы. Предварительный просмотр результата можно выполнить, нажав на кнопку Просмотр результата левой кнопкой мыши и удерживая ее.

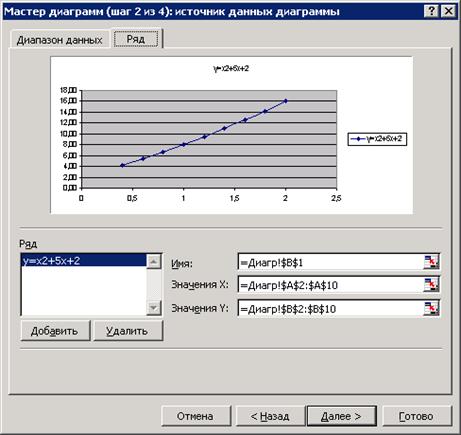
4. Шаг 2 мастера диаграмм: задать исходные данные. Здесь также можно задать подписи по оси Х: – выйти на рабочий лист и выделить нужные ячейки с текстом.

На этом шаге также задается имя каждого ряда и указываются его значения (если ячейки не были выделены раньше).

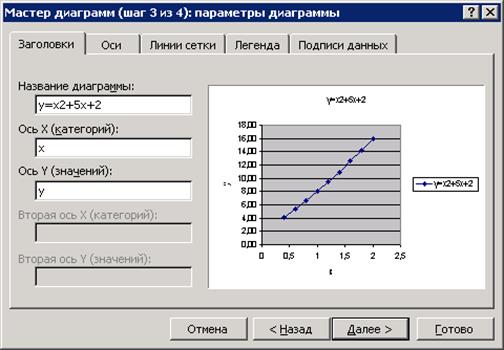
5. Шаг 3 мастера диаграмм: задать параметры диаграммы – ввести заголовки диаграммы и осей, выбрать режимы отображения линий сетки и подписей данных, определить местоположение легенды и т. д.

6. Шаг 4 мастера диаграмм: определить место размещения диаграммы.

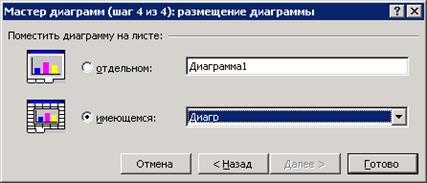
Готовую диаграмму можно изменить. Для работы с любым элементом диаграммы необходимо навести на него указатель мыши, щелчком правой кнопки мыши вызвать контекстное меню, в котором выбрать нужную команду.

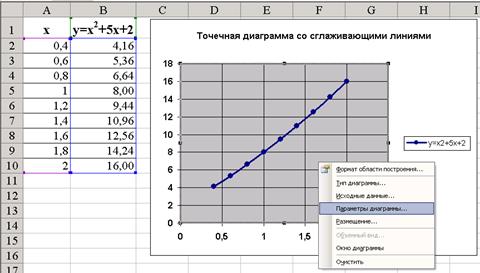
Построение линии тренда

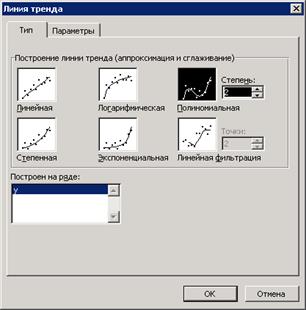
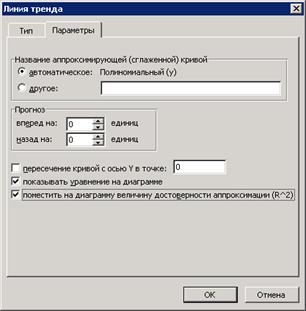
В случаях, когда диаграмма построена по эмпирическим данным, Excel позволяет получить линию тренда – аппроксимирующую функцию, характеризующую расположение точек. Для этого нужно щелкнуть на графике правой кнопкой мыши, выбрать Добавить линию тренда, определить тип зависимости (чаще всего полиномиальная) (рис. 2). Для получения уравнения линии тренда на вкладке Параметры необходимо установить флажки:

показать уравнение,

поместить на диаграмму величину достоверности аппроксимации R^2.

R^2 – это корреляционное отношение, чем оно ближе к 1, тем точнее аппроксимирующая функция описывает расположение точек. Если R^2=1, то аппроксимирующая функция полностью совпадает с точками графика.