Внешние характеристики газотурбинных установок

Внешние характеристики газотурбинных установок определяют важнейшие свойства ГТУ в разнообразных условиях их работы, в частности, отражают изменение ее мощности, крутящего момента, КПД от частоты вращения.

Изменение внешних характеристик для простоты рассуждений вначале целесообразно рассматривать на примере работы одной ступени при постоянном расходе рабочего тела и условии, что состояние газа на выходе из направляющего аппарата и рабочего колеса остаются неизменными.

При этих условиях (см. уравнение 2.4 ), вращающий момент на среднем радиусе r лопаточного колеса турбинной ступени при оптимальной частоте вращения n₀ или оптимальной скорости u₀ определяется уравнением Эйлера [2]:

М₀ = G (r₁ c_1,u,опт. – r₂ c_2,u,опт. ) = G (c_1,u,опт. – c_2,u) r (2.22)

или 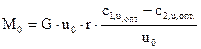(2.23)

Вращающий момент для любой скорости u можно выразить уравнением:

М = G (c_1,u,опт. - c_2,u,опт. + u₀ – u) r (2.24)

или

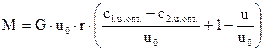(2.25)

Из последнего уравнения видно, что между вращающим моментом М и частотой вращения n существует линейная зависимость. Максимальное значение вращающий момент имеет при n = 0, а при условии u = u₀ + c_1,u.опт. – c_2,u,опт. он обращается в нуль (Рис. 2.9) [2]:

Из сопоставления уравнений (2.23) и (2.25) получим:

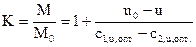(2.26)

Величина К характеризует приспособляемость двигателя к изменению внешней нагрузки.

Если во время работы турбины снять всю полезную нагрузку, а расход рабочего тела сохранить неизменным, то двигатель пойдет в разнос и хотя частота вращения при этом теоретически не будет возрастать бесконечно, но может достичь величины недопустимой с точки зрения прочности ГТУ.

Наличие прямолинейной тяговой характеристики газовой турбины (Рис. 2.9) приводит к тому, что на всех режимах работы агрегата, кроме одного (оптимального), имеет место потеря мощности и его КПД. Связано это опять же с резким изменением КПД турбины от характеристики u/c₁. Действительно, при с₁ = idem, изменение частоты вращения или, что то же самое, окружной скорости u приводит к резкому изменению мощности установки и ее КПД.

Обычно газотурбинная установка проектируется так, что режимы ее максимальной экономичности и оптимальной мощности совпадают с режимами максимальной частоты вращения. В этих условиях вся ее рабочая зона лежит на левой ветви кривой мощности (см. Рис. 2.9). Соотношение крутящих моментов в этом случае составляет 2-2,3, что является вполне удовлетворительным для условий работы ГТУ с мало меняющейся внешней нагрузкой, что имеет место, например, при их эксплуатации ГТУ на магистральных газопроводах.

Если принять во внимание, что мощность ГТУ зависит в основном от температурного перепада по турбине и расхода газов через турбину, то возможность изменения расхода газов при изменении частоты вращения турбины позволяет раздвинуть диапазон оптимальной мощности турбины в значительном диапазоне изменения частоты вращения (пунктирная трапеция, см. Рис. 2.9).

Мощность, развиваемая турбиной при различной частоте вращения, как известно, определяется соотношением:

N = M w (2.27)

Или в относительном виде:

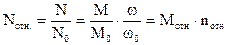(2.29)

с учетом уравнения (2.23), получим:

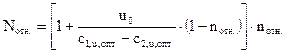(2.30)

из последнего уравнения видно, что кривая N_отн. = f (n_отн.) представляет собой параболу, причем максимальной значение N_отн. достигается при условии (¶ N_отн. / ¶n_отн. = 0), Рис 2.10

Переход от моментных характеристик одной ступени к параметрам многоступенчатой турбины в первом приближении осуществляется на основе принципа аддитивности энергетических функций. Работа многоступенчатой турбины представляется как сумма работ отдельных ступеней турбины:

H = å h_i (2.31)

Общий момент, развиваемый многоступенчатой турбиной определяется как сумма моментов ее отдельных ступеней:

М = åМ_i (2.32)

В многоступенчатой турбине имеет место сложное взаимодействие последовательно расположенных ступеней между собой. Здесь и так называемый коэффициент возврата теплоты и частичное использование кинетической энергии потока за рабочим колесом в следующей ступени, изменение пропускной способности турбины и т.п. Можно полагать, что увеличение числа ступеней приводит к улучшению тяговых свойств газотурбинной установки [2].