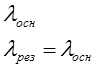Схема основных состояний технических систем в ССНТ

13 – повреждение 21 – восстановление

14 – отказ 23 – капитальный и средний ремонт

Наиболее важным событием при оценке надежности являются отказы технических средств.

По ССНТ различают следующие виды отказов:

- независимый [56] – отказ объекта не обусловленный отказом других объектов;

- зависимый [57] – отказ объекта, обусловленный отказом других объектов;

- внезапный [58] - отказ объекта характеризуется скачкообразным изменением значений одного или нескольких заданных параметров;

- постоянный [59] – отказ характеризует постоянное изменение значений заданных параметров;

- перемежающееся [60] – многократно возникающий и самоустраняющийся отказ объекта одного и того же характера (сбой).

Стандартом введены понятия конструктивного, эксплуатационного отказов.

1.5. Понятие простых и сложных систем.

По характеру проявления отказов технической системы:

Простые системы: система, полностью теряющая работоспособность при отказе ее элемента или продолжающая функционировать, если отказавший элемент зарезервирован.

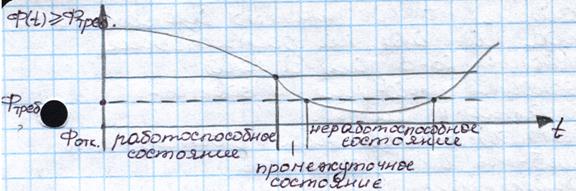
Сложная система: система, выполняющая свои функции при отказе одного или нескольких элементов, но с пониженной эффективностью. В сложных системах целесообразен переход к упрощенной модели, связанный выходной эффект системы 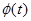с параметрами этой системы:

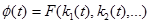
Отказом сложной системы считается событие, заключается в нарушении ее работоспособного состояния, приводимого к снижению показателей эффективности ниже заданного уровня.

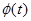- как правило, нормируется .

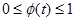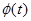Используется относительный критерий эффективности.

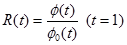
Интервальный критерий: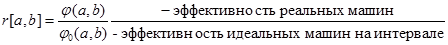

1.6. Качество функционирования АСУ и информационная безопасность автоматизированных информационных систем.

Качество функционирования АС – совокупность свойств, обуславливающих пригодность системы в течение своего жизненного цикла обеспечивать надежное и своевременное представление полной, достоверной и конфиденциальной информации для ее последующего целевого использования.

Проблема обеспечения качества функционирования АС не отделима от проблем гарантии ее информационной безопасности.

Информационная безопасность АС как свойство АС заключается в способности АС к предотвращению реализации потенциальных угроз, направленных на нарушение штатного режима, снижение качества функционирования АС и нейтрализации последствий негативного воздействия.

Требование по обеспечению безопасности АС всегда направлена на достижение 3-х основных свойств защищенной информации:

1. готовность информации и соответствующих автоматизированных служб

2. целостность информации: достоверность, безошибочность, актуальность.

3. Конфиденциальность (засекречивание информационного доступа тому, кому она предназначена).

Особенностью представленных проблем является возможность ущерба обществу и потребителям информации при сравнительно малых затратах на искажение, уничтожение информации.

Потенциальная возможность непреднамеренных негативных воздействий вынуждает резко активизировать исследования разработки и совершенствования методов и средств обеспечения защиты и безопасности.

Непрерывное повышение уровня автоматизации подготовки и принятие ответственных решений в системах государственного и военного управления все больше функций перекладывают на программную среду в соответствии с БД. В результате проблема обеспечения безопасности их функционирования сдвигается от лиц высокого ранга (принимающих важное решение) к лицам, непосредственно разрабатываемым методы и средства автоматизации выработки ответственных решений. При этом понижается уровень ответственности в системной классификации лиц, от которого зависят стратегически важные решения, т.к. некоторые простейшие ошибки могут привести к катастрофам. Возрастание важности задач, возлагаемых на АС сопровождается увеличением их уязвимости от предумышленных внешних воздействий.

Неспособность реализованных в АС технологий сбора, хранения и обработки информации обеспечить в реальных условиях функция АС надежное и своевременное представление информации и свидетельствует о недостаточности принятых при разработки программных и технических средств.

1.7. Общие понятия об оценке надежности АСУ.

Надежность представлений АС информации: свойство программ технических (ПТС) АС обеспечить прием, автоматическую обработку запроса и предоставление выходной информации согласно реализованному алгоритму при соблюдении экс-ых условий изменений и технического обслуживанию АС.

Для оценки надежности представления выходной информации в АС принята следующая модель: в любой момент времени ПТС АС находится в одном из двух чередующихся состояний – работоспособном и неработоспособном. Математическое ожидание времени пребывания ПТС в работоспособном состоянии = средней наработки на отказ. Математическое ожидание времени пребывания ПТС в нерабочем состоянии = среднему времени восстановления работоспособного состояния. В случайный момент времени пользователь направляет запрос на предоставление выходного документа.

3 варианта:

1. запрос поступает в момент работоспособного состояния;

2. запрос поступает в период работоспособного состояния, но АС находится в этом состоянии менее времени, необходимого для обработки запроса;

3. запрос поступает в период неработоспособного состояния.

1) – надежное предоставление информации

2,3) – не предоставляет запрашиваемой информации

Полученные в ходе проведения испытаний оценки математического ожидания работоспособного и неработоспособного состояния, являются исходными данными для расчета надежности представления выходной информации в АС.

Выходная информация разбивается на типы, определяемые формами выходных данных.

RAS-технология: надежность, готовность и качество.

Количественные показатели надежности.

2.0. Классификация количественных показателей надежности объекта по ССНТ.

[25] Показатель надежности – количественная характеристика одного или нескольких свойств, составляющих надежность объекта.

[26] Единичный показатель – характеристика одного свойства (среднее время восстановления T_в)

[27] Комплексные показатели – характеристики нескольких свойств надежности (коэффициент надежности)

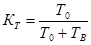- время рабочего состояния.

30.10.02г

Схема классификации показателей по ССНТ 27002-87.

Показатели надежности [25].

Единичные показатели [26]
Показатели безотказности 2.1.	Показатели долговечности 2.2.	Показатели ремонтопригодности 2.3.	Показатели сохранности 2.4.
1. вероятность безотказной работы [35] *	1. средний ресурс [41]	1. вероятность восстановления работоспособного состояния [47]	1. срок сохранности [49]
2. вероятность отказа *	2. g-%-й ресурс [42]	2. среднее время восстановления работоспособного состояния [48]	2. g-%-й срок сохранности [50]
3. средняя наработка до отказа [36] *	3. назначенный ресурс [43]	3. интенсивность восстановления
4. интенсивность отказов [39] *	4. средний срок службы [44]
5. гамма %-я наработка до отказа [37] *	5. g-%-й срок службы [45]
6. средняя наработка на отказ [38] **	6. назначенный срок службы [46]
7. параметр потока отказов [40] **
* - не восстанавливаемые ** - восстанавливаемые

Комплексные показатели:

1. 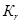- коэффициент готовности [51]

2. коэффициент оперативной готовности [52]

3. коэффициент технического использования [53]

4. коэффициент использования

5. коэффициент планового применения [54]

6. коэффициент сохранения эффективности [55].

2.1. Показатели безотказности объекта.

Безотказность [2] – свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или наработки.

Наработка [28] - продолжительность или объем работы. Наработка неразрывно связана с понятием «отказ». Появление отказов (вероятность) исчерпывающе описывается законами распределения случайных величин, а для оперативных оценок – моментами СВ. Наиболее полно изучены методы оценки появления отказов – не связанные со строением элементов.

2.1.1. Вероятность безотказной работы.

[35] – вероятность того, что в пределах заданной наработки отказ не возникнет. Вероятность отказа и вероятность безотказной работы всегда образуют полную группу событий: .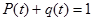

Вероятность отказа 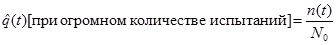, где n(t) – число отказов в интервале [0;t], N₀ – число наблюдаемых объектов.

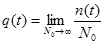
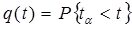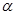, - рубеж, при котором вычисляется отказ при t=0, q(t)=0

t=¥, q(t)=1.

q(t) описывается интегральным законом распределения этой величины

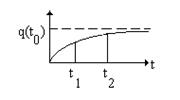q (t₁;t₂)=q(t₂)-q(t₁)

p(t) – вероятность безотказной работы:

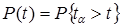
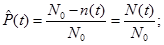- число отказов до t.

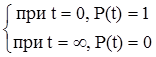
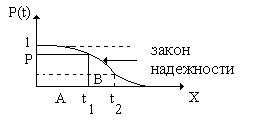
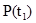- вероятность того, что не откажет на интервале [0; ].

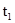Совместное наступление событий А и В Þ Р(А В)=Р(А) × Р_А(В)

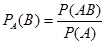
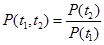
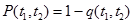
2.1.2. Частота отказов f(t) – отношение числа отказавших элементов в некотором интервале Dt к первоначальному числу отказавших элементов.

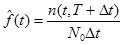, где t – начало интервала измерения.

Определим связь между f(t), P(t), q(t).

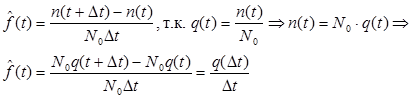
при Dt®0

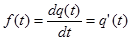! ; т.е. соотношение интегрирования и дифференцирования.

!

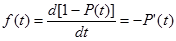
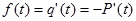
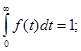
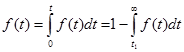
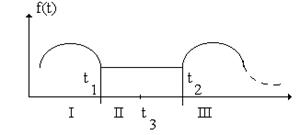
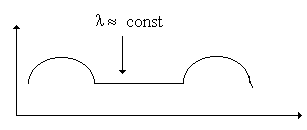
1 этап – область проработки

2 этап – область нормальной эксплуатации объекта

3 этап – старение (износ) и интенсивные отказы.

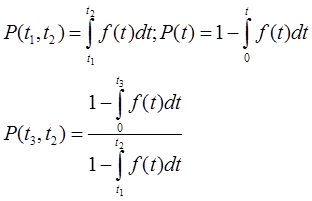
2.1.3. Интенсивность отказов [39].

l(t) – условная плотность вероятности возникновения отказов невосстанавливаемых объектов, определенная для рассматриваемого момента времени t, при условии, что до этого момента отказ не возникал.

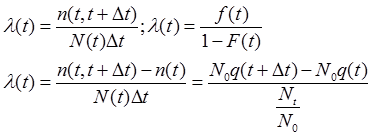
при t®0

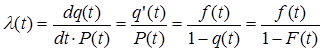
2.1.4. Закон надежности – зависимость вероятностей от f.

Определить зависимость P(t) от .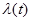

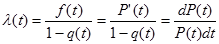
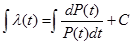- табличное f Þ

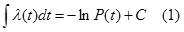
при начальных условиях с=0.

Из выражения (1) Þ, что

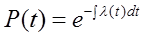
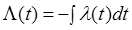
при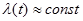

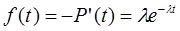
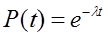
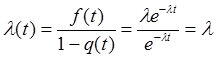
2.1.5. Средняя наработка до отказа [36] – математическое ожидание этой наработки.

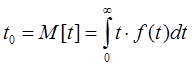Определение взаимн. t₀ и P(t)

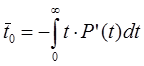беря по частям:

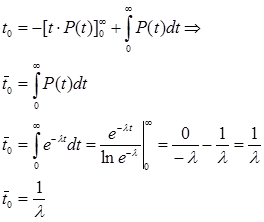
06.11.02г

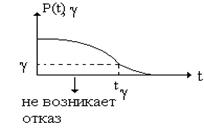
[36] g-%-я наработка до отказа – наработка, в течение которой отказ не возникает с вероятностью g, выраженной в %

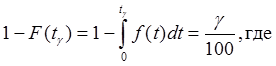
t_g-g-% наработка;

g - вероятность, выраженная в %.

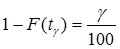
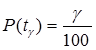, при экспоненциальном законе распределения (l=const).

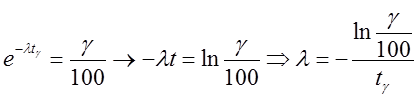
Примеры простейших постановок надежности.

I. Определить вероятность безотказной работы за 100 часов наработки при интенсивности отказов 250×10^{-6 1}/_ч.

- Закон е-й Þ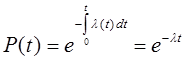

Р(100)=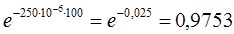

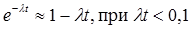
II. Определить интенсивность отказа устройства, обеспечивающего 10 часов наработки до отказа с вероятностью 0,999.

- Примем экспоненциальный закон надежности

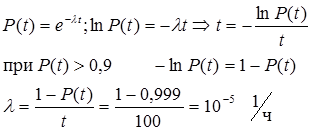
III. Определить наработку дисковода, достигнутую с вероятностью 0,99; 0,999; 0,9999.

При рекламе среднего времени наработки на отказ 28 лет (250 000 часов).

При е-м законе распределения определяем нагрузку до отказа:

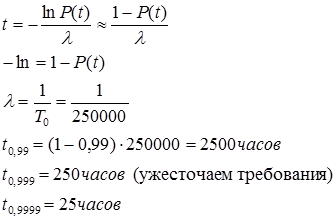
IV. Прогнозирование надежности. Используя подтвержденную наработку устройства = 1000 часов с вероятностью 0,99. Какова вероятность безотказной работы его за 10000часов. При е-м законе распределения

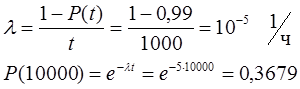
V. Определить g-% медианную наработку на контакт разъема при интенсивности отказа контакта l=6×10^{-6 1}/_ч.

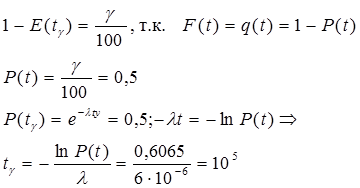
2.1.7. Ориентировочная оценка реальной интенсивности отказа.

Оценка определяется умножением номинальной интенсивности отказов на поправочные коэффициенты внешнего взаимодействия и режим работы объекта.

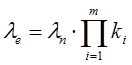, где k_i – поправочные коэффициенты

l_е – реальное интенсивность отказов

l_n – номинальная интенсивность отказов

Для всех k_i >1.

Для k_p – коэффициент режима работ. Перегрузка k_p >1, облегченный режим k_p <1.

Поправочные коэффициенты учитывают:

1) естественные условия (климат, биологические, космические, высотные и т.д.)

2) эксплуатационные (электромагнитные поля, помехи электрические, механические и т.д.)

13.11.02г.

2.2. Показатели надежности.

Долговечность [3] – свойство объема сохранять работоспособное состояние до наступления предельного состояния при установленной системе обслуживания и ремонта.

Показатели долговечности основываются на двух понятиях стандарта:

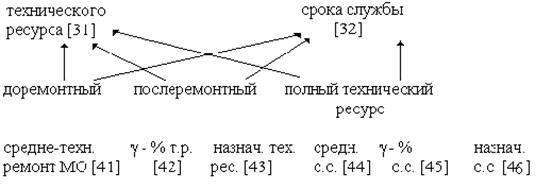
- технический ресурс [31]

- срок службы [32]

Техническим ресурсом называется наработка объема от начала его эксплуатации или ее возобновления после ремонта определенного вида до перехода в предельное состояние.

Срок службы – календарная продолжительность эксплуатации объема от начала его эксплуатации или его возобновления после ремонта определенного вида до перехода в предельное состояние.

Схема наименований показателей долговечностей.

Показатели долговечности.

Средний технический ресурс [MO].

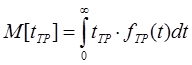
g-% технический ресурс

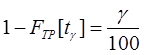
2.3. показатели ремонтопригодности, показатели восстанавливаемости.

2.3.1. Понятие ремонтопригодности и восстанавливаемости.

Ремонтопригодность [4] – свойство объекта, заключающиеся в приспособленности к предупреждению и обнаружении, возникновение отказа, поддержание и восстановление работоспособного состояния, проведение технического обслуживания и ремонта.

В электронной аппаратуре используются следующие свойства ремонтопригодности: контролируемость, доступность, легкосъемность, взаимозаменяемость и восстанавливаемость.

Ремонтируемый объекта [23] – это объект, для которого проведение ремонта предусмотрено.

Восстанавливаемый объект [21] – это объект, для которого в рассматриваемой ситуации проведение восстановления работоспособного состояния предусмотрено НТД и КД.

Невосстанавливаемый объект [22] – тоже восстановление не предусмотрено НТД и КД.

При ремонтах различают:

- восстанавливаемый ремонт;

- текущий и средний ремонт;

- капитальный ремонт.

2.3.2. Вероятность восстановления.

Вероятность восстановления [47] – вероятность того, что время восстановления не превышает заданного.

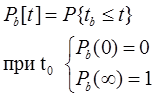
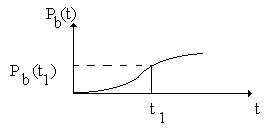
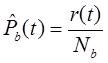
r(t) – число восстановленных элементов в интервале [0,t).

N_b – общее количество восстановленных элементов.

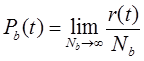
V_b(t) – вероятность невосстановления.

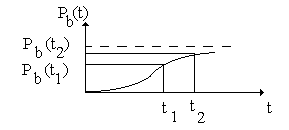
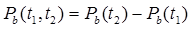
2.3.3. Среднее время восстановления работоспособного состояния [48].

Это математическое ожидание вероятности восстановления работоспособного состояния.

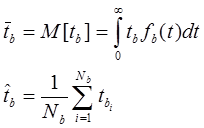
По аналогии со среднем временем отказа, математическое ожидание времени восстановления можно получить:

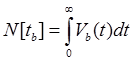
2.3.4. Частота и интенсивность восстановления вне ССНТ для аналитических расчетов.

По аналогии с понятием частоты интенсивности отказов вводится интенсивность восстановления.

Частота восстановления – это отношение числа восстановительных объектов в интервале Dt к первоначальному числу восстанавливаемых объектов.

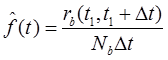
r_b(t) – число восстановленных элементов и интервале

f_b(t) – по аналогии с доказательством для частоты отказов.

Интенсивность восстановления – условная плотность вероятности восстановления объекта для рассматриваемого момента времени, при условии, что до этого момента восстановление не произошло.

По аналогии с интенсивностью отказов можно записать:

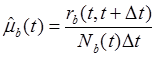,где

N_b – число восстановленных элементов на интервале [0,t).

Сравнение формул аналитического вычисления l(t) и m(t).

Показатели отказов	Показатели восстановления
q(t)+P(t)=1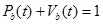
f(t)=q’(t)= - P’(t)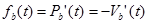
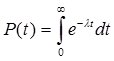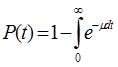Для l(t)»const	Для m(t)»const

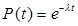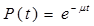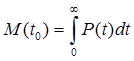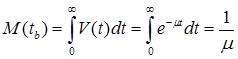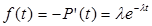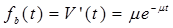Практически закон восстановления электронной аппаратуры приближается

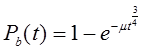
Для многих случаев обнаружения отказов, восстановление и т.д. удобен закон распределения Вейбула.

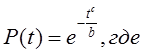c и b – параметры закона.

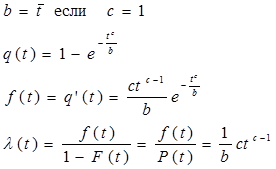
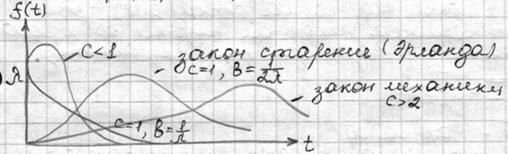
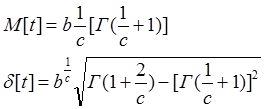
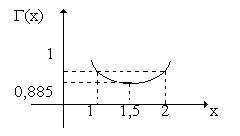
Г(х) – табулированная функция, имеющая расчет 1<x<2.

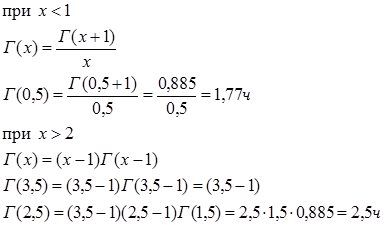
2.3.5. Средняя наработка на отказ восстанавливаемых объектов.

Средняя наработка на отказ и до отказа практически равные величины на участке нормальной эксплуатации.

Средняя наработка на отказ [38] – это отношение некоторой наработки объекта к математическому ожиданию числа отказов за эту наработку.

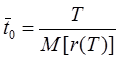
T – наработка объекта.

r(t) – число отказов в интервале [0,t)

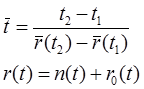
n(t) – число отказов из первоначального множества объектов числа отказов.

r₀(t) – число отказов среди восстановленных объектов.

В фундаментальной и элементарной теории восстановление доказывается, что:

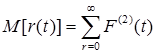
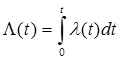- ведущая функция

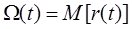
2.3.6. Параметр потока отказов восстанавливаемых систем.

Интенсивность отказов для восстановленных и не восстановленных систем одинакова на участке эксплуатации. Поэтому ССНТ вводит параметр потока отказов [40] справедливого для любого участка эксплуатации.

Параметр потока отказа – это отношение среднего числа отказов за произвольное малую наработку к значению этой наработки.

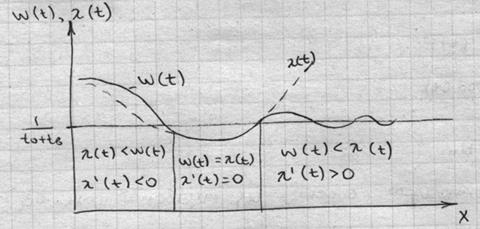
Можно показать, что у параметра потока отказа существует предел:

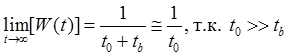
2.4. Показатели сохраняемости.

Сохраняемость [5] – свойство объекта сохранять значение показателей безотказности, долговечности и ремонтопригодности в течение и после хранения и/или транспортировки.

Срок сохраняемости – календарная продолжительность сохраняемости, входящая в срок службы.

Средний срок сохраняемости [49].

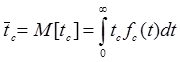
t_c – срок сохраняемости

f_c(t) – дифференциальный закон распределения.

g-% срок сохраняемости [50] - срок сохраняемости, достигаемый с заданной вероятностью g, выраженной в процентах.

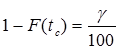
2.5. Комплексные показатели.

2.5.1. Фонд рабочего времени tн определяется формулой

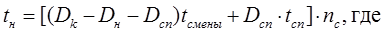
D_k – число календарных дней в фонде

D_н – нерабочие дни

D_сп – число дней с сокращенной продолжительностью

t_смены – продолжительность смены

t_сп – время работы смены с сокращенной продолжительностью

n_с – число смен

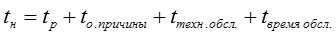
t_р – время работы объекта

t_орг – время задержки по организационным причинам

t_то – время технического обслуживания

t_в – время восстановления

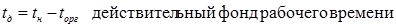
20.11.02г

На основании понятия фонда рабочего времени вводятся показатели надежности (комплексные):

1. коэффициент использования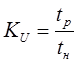

2. коэффициент технического использования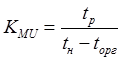

3. коэффициент готовности – вероятность работоспособного состояния объекта в произвольный момент времени в установленном режиме эксплуатации.

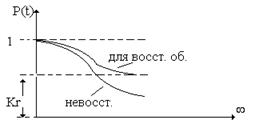
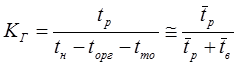
4. Коэффициент оперативной готовности – вероятность работоспособного состояния в произвольный момент времени с учетом сохранения работоспособного состояния в интервале (0; t) с момента включения объекта.

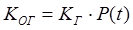
В справочниках различают стационарный

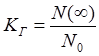
N₀ – исходное число элементов

N(¥) – число не отказавших элементов

Нестационарный:

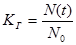
N(t) – число не отказавших элементов

5. Коэффициент планового использования – доля периода эксплуатации без учета задержек по организационным причинам.

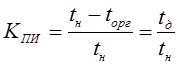
6. Коэффициент сохранения эффективности – отношение наработки реальной системы в некотором интервале к значению этой же наработки идеальной системы (надежность=1)

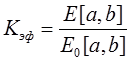
[a,b] – интервал наработки.

Пример.

Интервальная оценка безотказности работы по распределению Вейбула с параметрами c=2, b=0,5×10⁴. Интервал времени t₁=30ч, t₂=50ч.

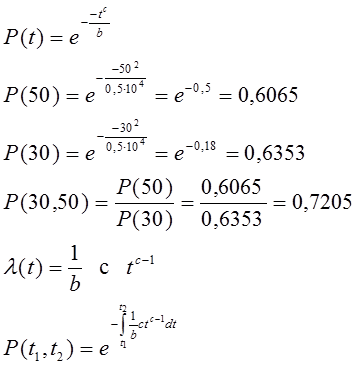
Найти среднее время наработки на отказ при распределении Вейбула с параметрами c=2, b=0,16×10⁴.

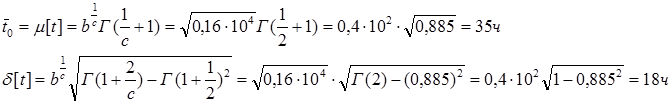
Оценка надежности систем с элементами конечной надежности.

3.1. Понятие и способы резервирования.

Резервирование [66] – применение дополнительных средств и/или возможностей с целью сохранения работоспособного состояния одного или нескольких элементов.

Резерв [70] – совокупность средств и/или возможностей для резервирования.

Виды резервов:

1. структурное резервирование [77] – резервирование с применением резервных элементов структуры;

2. временное резервирование – применение резерва времени для выполнения задачи;

3. информационное резервирование [79] – резервирование с применением информационной избыточности.

4. функциональное резервирование [80] – резервирование с применением многофункциональных элементов.

При резервировании вводится понятие:

Основной элемент [67] – элемент структуры, необходимый для выполнения объектом требований функций при отсутствии отказов его элементов.

Резервный элемент [68] – элемент структуры, предназначенный для выполнения функций основного элемента в случае отказа основного элемента.

Кратность резервирования [76] – отношение числа резервных элементов r к числу оставшихся элементов n, выраженная дробью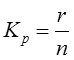

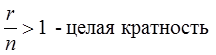
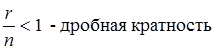
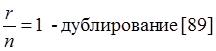
Восстанавливающийся резерв [74] – резерв, подлежащий восстановлению.

Невосстанавливающийся резерв [75] – не подлежит восстановлению.

Различают:

Общее резервирование [82] – резервирование элемент – объект в целом.

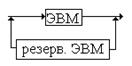
Раздельное резервирование [83] – резервный элемент – отдельный элемент или их группа.

Смешанное резервирование [84] – сочетание видов резервирования.

В структуре объекта различают:

Постоянное резервирование – резервирование без перестройки структуры при возникновении отказа.

Динамическое резервирование [85] – резервирование с перестройкой структуры объекта при возникновении отказа.

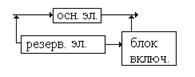
Динамическое резервирование может быть резервированием, замещением [86] и скользящим резервированием.

27.11.02г

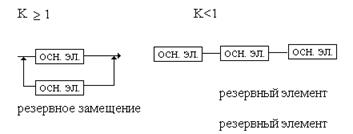
Динамическое резервирование замещением – функции основного элемента передаются резервному после отказа основного элемента.

Резервирование скользящее – группа основных элементов резервируется одним или несколькими элементами, каждый из которых может замещать любой отказавший элемент. При расчете надежности должно учитываться состояние резервного элемента по нагруженности, поэтому стандарт различает виды нагруженности резерва:

1. нагруженный резерв (горячий) [71] – резерв, который содержит один или несколько резервных элементов, находящихся в режиме основного элемента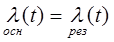

2. облегченный резерв (теплый) [72] -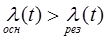

3. ненагруженный резерв (холодный) [73] -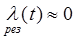

3.2. Оценка надежности систем методом структурных схем надежности.

3.2.1. Основные положения метода:

Система представляется схемой соединения элементов в виде двухполосного графа, имеющего один вход и один выход.

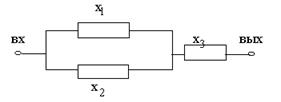
3.2.2. Структурная схема надежности представляется соединением элементов с точки зрения выполнения ими основных или резервных функций с постоянным включением.

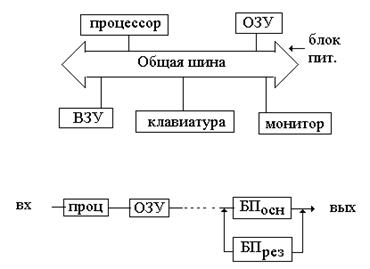
3.2.3. Система считается работоспособной, если между входом и выходом существует связанность графа хотя бы по одному пути.

3.2.4. Работоспособное состояние элемента условно обозначается наличие пути, называемое короткое замыкание (КЗ), а неработоспособное состояние – отсутствием пути, называемое обрыв.

3.2.5. Отказы элементов считаются независимыми

3.2.6. Метод позволяет определить вероятность P_s(t) безотказной работы системы в интервале (0,t), если заданы вероятности безотказной работы элементов в этом интервале P_i(t) или коэффициенты готовности K_r.

3.2.7. Метод не позволяет определять вероятность всех состояний системы из N элементов в виде функции времени кроме основного случая без резервирования.

2ⁿ – число состояний элемента

n – число элементов

3.3. Надежность системы с последовательным включением элементов.

По аксиоме умножения вероятностей

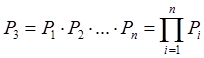
P_i – вероятное работоспособное состояние элемента.

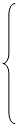3.4. Надежность системы с параллельно включенными элементами.

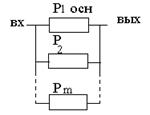
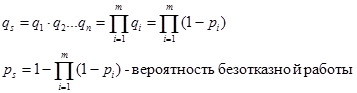
3.5. Смешанное соединение

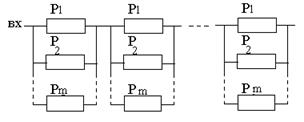
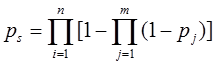
3.6. Система с мостиковыми элементами.

Применяется метод структурной декомпозиции, основанный на теореме:

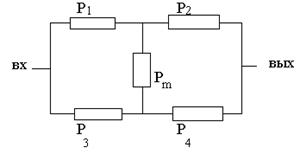
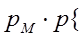
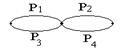
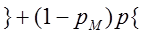
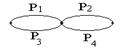
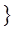
Н₁ Р_м

Н₂ (1- Р_м)

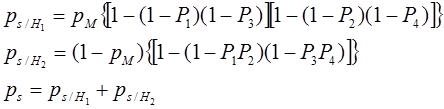
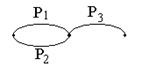
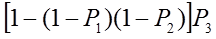
3.7. Схемы с узловыми элементами.

Сложные схемы с узловыми и мостиковыми элементами представляется в виде смешанного соединения и суммированием их по всем гипотезам.

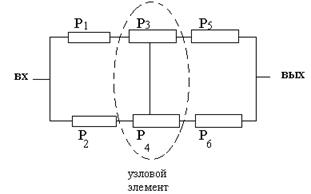
Гипотезы состояний:

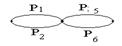
Н₁ оба исправны

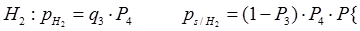
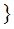
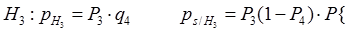
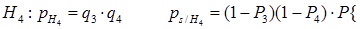
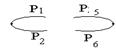
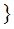
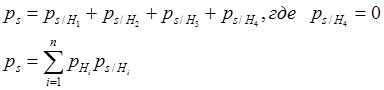
n – число гипотез

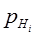– вероятность гипотезы

Главное при решении схем с узловыми элементами сделать правильный выбор узлового элемента, позволяющий представить общую схему в виде композиции последовательно-параллельных схем.

3.8. Матричный метод расчета схем произвольной структуры.

Метод позволяет оценить надежность системы с учетом зависимости отказов.

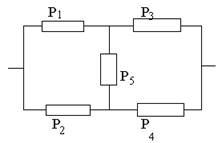
Система из 5 элементов может находиться в 32 состояниях (2⁵). Эти состояния рассматриваются как гипотезы, при которых определяется вероятность работоспособного состояния схемы в целом.

Н_i i=0,3

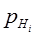
Нi	Состояние системы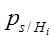
эл1	эл2	эл3	эл4	эл5

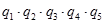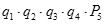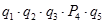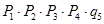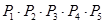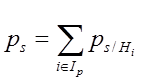
I_р – область работоспособного состояния

P_s – надежность исходной системы (вероятность работоспособного состояния)

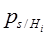- вероятность работоспособного состояния исходной системы при i-той гипотезе

I_р – множество гипотез, при которых обеспечивается связность графа исходной системы

3.9. Верхняя и нижняя оценка надежности по схеме Эзари-Прошана (Литвака-Ушакова).

Оценка основывается на теоремах о минимальных путях и минимальных разрезов графа с надежными ребрами.

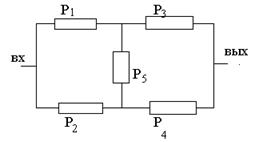
Минимальный путь – путь без петель и контуров, кратчайший путь вход-выход.

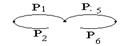
1 путь Р₁-Р₃

2 путь Р₂-Р₄

3 путь Р₁-Р₅-Р₄

4 путь Р₂-Р₅-Р₃

Минимальные разрезы – разрезы с минимальным числом элементов, нарушающих связность графа.

1 разрез q₁-q₂

2 разрез q₃-q₄

3 разрез q₁-q₅-q₄

4 разрез q₂-q₅-q₃

Доказывается следующее неравенство:

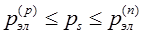
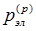- граница, определяемая разрезами

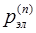- граница, определяемая минимальными путями

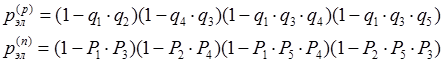
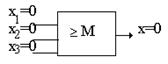
Резервирование с применением адаптивных структур (мажиритарное резервирование два из трех)

3.10. Надежность систем со скользящим резервированием.

3.10.1. Нагруженный резерв равнонадёжных элементов с экспоненциальным распределением вероятности отказов.

P_i=P

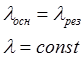
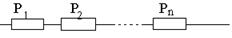
n_осн

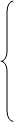
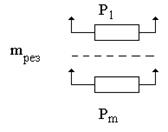
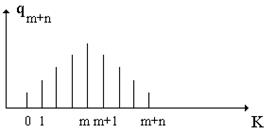
По формуле Бернулли, описывающей данную схему

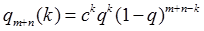
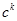- число сочетаний

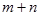- число элементов

k – количество событий

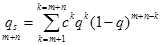
k³m+1 – система не работоспособна

k – число событий, приводящих к отказу системы

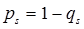
3.10.2. Надежность системы с ненагруженным резервом, равнонадёжными элементами.

P_i=P

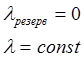
Вероятность появления ровно «k» событий по закону Пуассона выражается формулой:

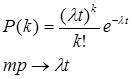
Вероятность безотказной работы группы из n элементов

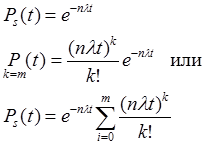
04.12.02г

4. Марковские модели надежности с непрерывным временем и дискретным счетным множеством состояний.

Задача исследования модели надежности состоит в нахождении функции или алгоритма определения вероятности состояния системы в любой произвольный момент времени или на любом дискретном шаге процесса скачкообразного перехода системы из одного состояния в другое под воздействием случайных факторов.

Эта задача значительно упрощается, если случайные процессы сводятся к Марковским, т.е. представление процесса как результата воздействия Пуассоновских потоков отказа и восстановления (простейший поток с ординарностью, стационарностью и без последствия).

Т.е.:

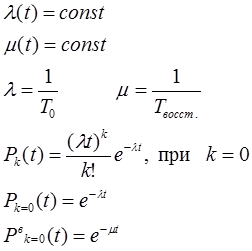
Система Марковских процессов удобно представить в виде размеченного графа вида:

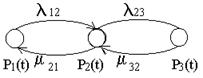
Задан объект, подлежащий исследованию и Пуассоновские потоки l и m.

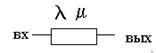
Определим функции состояния объекта во времени для неработоспособного состояния.

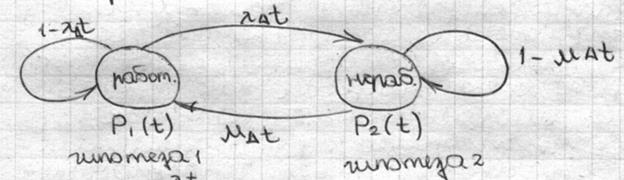
Составим граф поведения объекта во времени

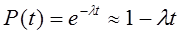
По формуле полной вероятности запишем уравнение состояний системы в конечных приращениях:

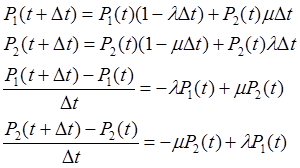
при Dt®0 получаем уравнение Колмогорова, описывающее состояние системы.

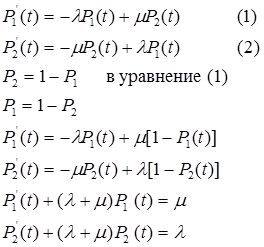
Решение этих уравнений прямой подстановкой в формулу Лагранжа получаем следующие функции надежности для первого и второго состояния после вычисления постоянной интегрирования в момент времени t=0.

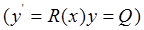
При t=0 и вероятности :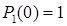

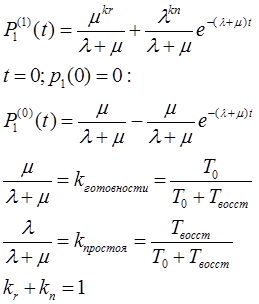
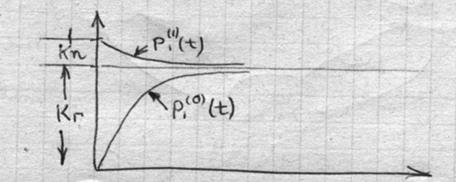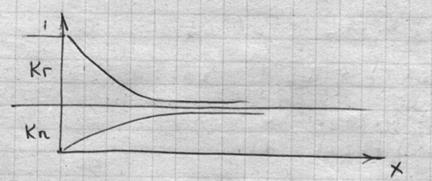Для состояния P₂(t) принципиально кривые остаются аналогичными.

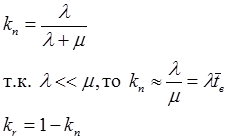
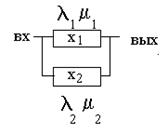
Модель восстанавливаемой системы с двумя параллельно включенными элементами.

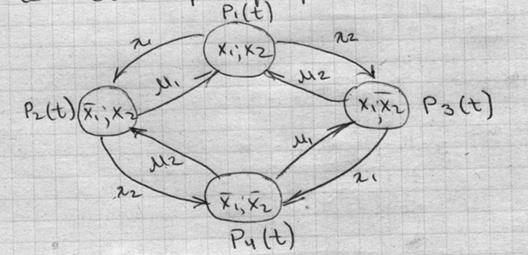Гипотеза состояний системы составим граф состояния системы:

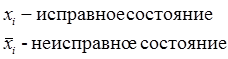
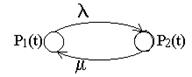
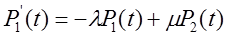
На основании уравнения Колмогорова:

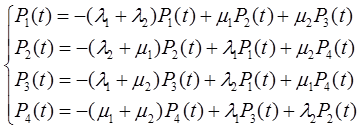
В результате решения уравнений в установившемся режиме, т.е. через k_n и k_r, получаем следующее соотношение:

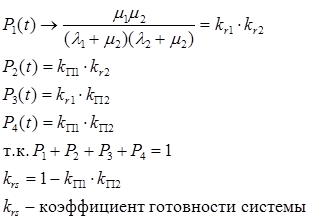
Для случая дублирования в справочниках приводится формула вероятности состояния системы (работоспособное) в нагруженном и ненагруженном резерве.

Приближенная формула расчета надежности для n включенных элементов (параллельно).

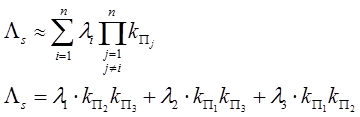
11.12.02г

Понятие о финальных вероятностях и системах с доходами.

Теорема о существовании в установившемся режиме финальных вероятностях состояния системы. Финальные вероятности существуют, если число состояний системы конечно и из каждого состояния в другое можно перейти за конечный интервал времени, т.е. .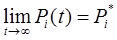

В этом случае дифференциальные уравнения Колмогорова могут быть представлены системой алгебраических уравнений. Для рассмотрения случая с n=2:

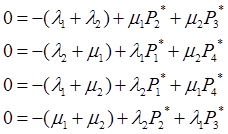
Полученная система без правой части решается с нормирующим условием:

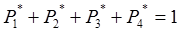
Решение этого уравнения дает значения финальных вероятностей.

Понятие о системах с доходами.

Финальные вероятности – среднее время нахождения системы в i-том состоянии. Следовательно, при доходе системы с_i в единицу времени в i-том состоянии Þ суммарный доход системы:

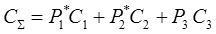
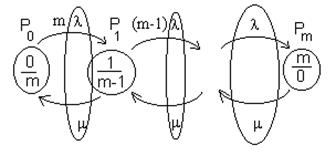
5. Схема гибели-размножения в моделях надежности.

5.1. Понятие системы гибель-размножение.

Дана группа из m однородных элементов, при Пуассоновских потоках отказов- восстановления группу элементов (организмов) можно представить графом-схема «гибель-размножение».

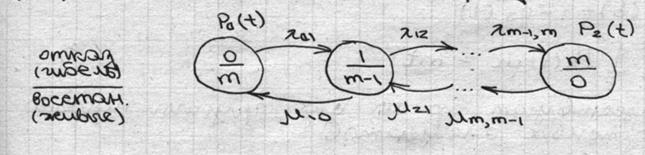
при n=4

2⁴=16 дифференциальное уравнение

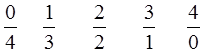
5.2. Схема с ненагруженным (холодным) резервом для группы m равнонадёжных элементов.

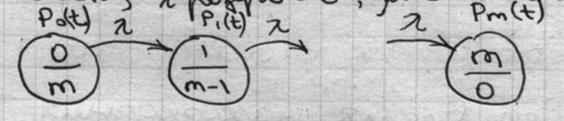
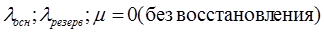
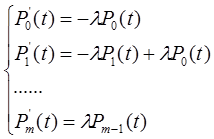
Система решается преобразованием Лапласа:

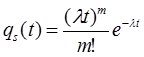
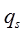- отказ системы

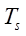- среднее время работы системы, увеличивающееся пропорционально числу резервных элементов

t – среднее время безотказной работы одного элемента

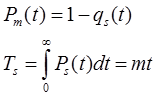
Существуют формулы для группы неравнонадёжных элементов.

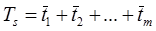, где t_i наработка до отказа I-того элемента (для неравнонадежных элементов).

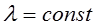
5.3. Нагруженный резерв равнонадёжных невосстанавливаемых элементов.

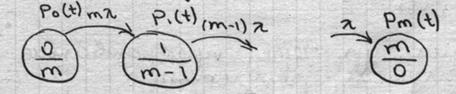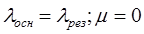
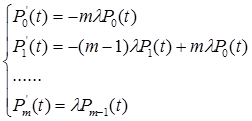
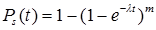для равнонадежных элементов

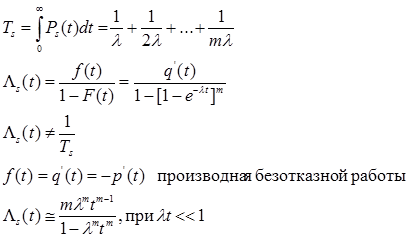
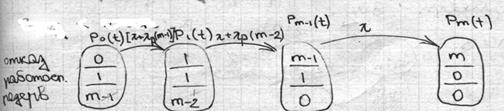5.4. Модель равнооблегченного резервирования и равнонадежной невосстанавливаемости элементов.

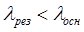
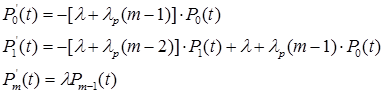
Решением дифференциальных уравнений через преобразование Лапласа получаем результат:

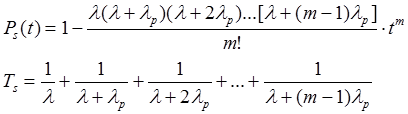
Включение результирующих элементов при облегченном резервировании дает наибольший эффект при:

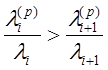
6. Марковские модели надежности с дискретным временем.

Процесс перехода физической системы из одного состояния в другое можно рассматривать в фиксированные моменты времени, следующие друг за другом через определенные интервалы времени (шаги процесса), в течение шага система находится в неизменном состоянии. Граф связности имеет вид:

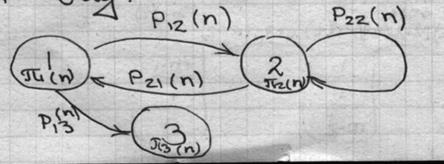m=3

P_ij(n) – вероятность перехода из i-того состояния в j-тое на n-ном шаге.

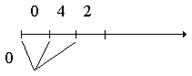
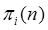- вероятность i-того состояния системы

i=1,m

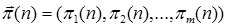
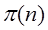- вектор состояния системы на n-ном шаге.

Переход системы из состояния в состояние определяется матрицей переходных вероятностей на n-ном шаге.

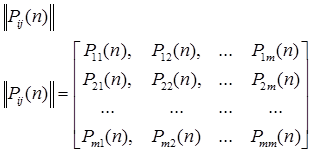
Если матрица переходных вероятностей не меняется от шага к шагу, то такой процесс перехода называется однородным.

При Пуассоновских потоках отказа-восстановления, процесс всегда однороден.

Алгоритм определения состояний системы на заданном шаге.

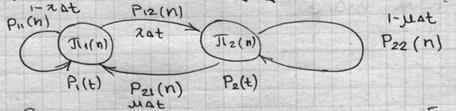Если можно определить вероятность системы на n-ном шаге и существует алгоритм на n+1 шаге, то случайный процесс определен на любом шаге.

Дана система с двумя состояниями m=2.

Разностные уравнения для аналогичной системы на интервале Dt имеет вид

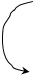
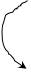
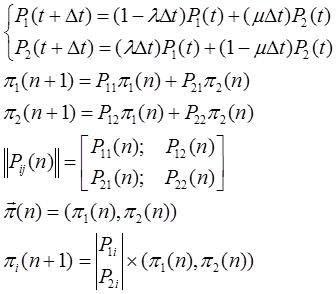
Таким образом, K-тое состояние системы есть произведение k-того столбца матрицы переходных состояний на вектор состояния системы.

Т.е. для общего случая:

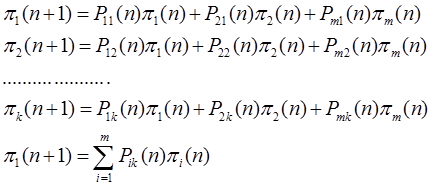
Векторная форма записи для однородных процессов:

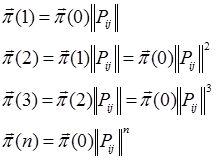
Существует уравнение Чеминема-Колмогорова для записи n-ого состояния системы для неоднородных процессов.

Понятие финальных вероятностей эргодических процессов.

Существует большой класс систем, у которых после некоторого числа переходов, вероятность 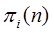стремится к постоянной величине.

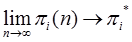
Также системы называются эргодическими или статистически устойчивыми. При этом различаются невозвратные состояния – состояния, в которых находится система как угодно долго без перехода в эргодический класс.

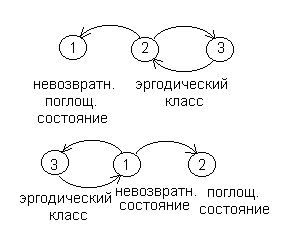
Каждый Марковский процесс должен иметь, по крайней мере, один эргодический класс.

7. Марковские модели надежности восстанавливаемых систем с финальными вероятностями.

Если граф состояния восстанавливаемой системы можно представить в виде схемы гибели-размножения, то в ряде случаев удается получить инженерные формулы расчета финальных вероятностей путем решения системы алгебраических уравнений.

Ограничения:

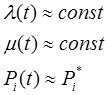
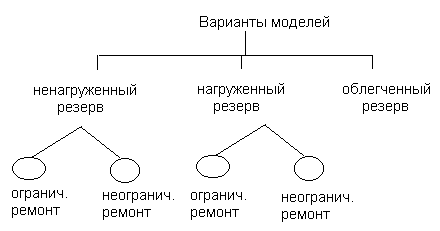
Ограниченный ремонт – одновременно восстанавливается только один отказавший элемент.

Неограниченный ремонт – одновременное восстановление всех отказавших элементов.

Ненагруженный резерв, ограниченный ремонт равнонадёжных элементов.

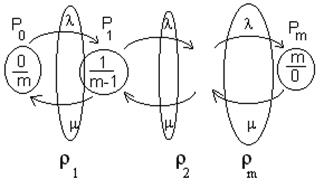
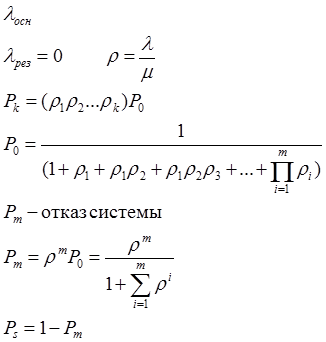
Ненагруженный резерв, неограниченный ремонт равнонадёжных элементов.

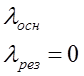
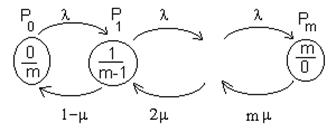
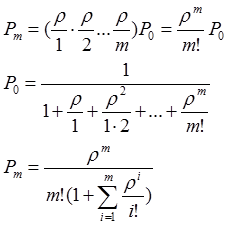
Нагруженный резерв ограниченный ремонт равнонадёжных элементов.